I. Hàm số và đồ thị
1. Hàm số
Định nghĩa
Nếu với mỗi giá trị của x thuộc tập hợp số D có một và chỉ một giá trị tương ứng của y thuộc tập
số thực R thì ta có một hàm số.
Kí hiệu: \(y = f\left( x \right)\).
Ta gọi x là biến số và y là hàm số của x.
Tập hợp D gọi là tập xác định của hàm số.
Tập tất cả các giá trị y nhận được, gọi là tập giá trị của hàm số.
2. Đồ thị của hàm số
Đồ thị của hàm số \(y = f\left( x \right)\) xác định trên tập \(D\) là tập hợp tất cả các điểm \(M\left( {x;f(x)} \right)\) trên mặt phẳng toạ độ với mọi \(x \in D\).
3. Sự biến thiên
Cho hàm số \(y = f\left( x \right)\) xác định trên khoảng \(\left( {a;b} \right)\).
- Hàm số \(y = f\left( x \right)\) đồng biến (tăng) trên \(\left( {a;b} \right)\) nếu:
\(\forall {x_1},{x_2} \in K:{x_1} < {x_2} \Rightarrow f({x_1}) < f({x_2})\)
- Hàm số \(y = f\left( x \right)\) nghịch biến (giảm) trên \(\left( {a;b} \right)\) nếu:\(\forall {x_1},{x_2} \in K:{x_1} < {x_2} \Rightarrow f({x_1}) > f({x_2})\)
II. Hàm số bậc hai. Đồ thị hàm số bậc hai và ứng dụng
1. Hàm số bậc hai
Định nghĩa
- Hàm số bậc hai là hàm số được cho bằng biểu thức có dạng \(y = a{x^2} + bx + c\left( {a \ne 0} \right)\).
Trong đó \(x\) là biến số, a, b, c là các hằng số.
- TXĐ: \(D = \mathbb{R}\).
2. Đồ thị hàm số bậc hai
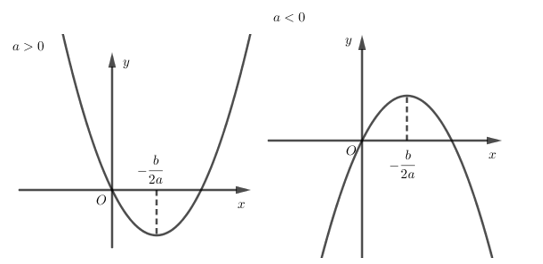
- Có dáng là đường Parabol có đỉnh \(\left( { - \dfrac{b}{{2a}}; - \dfrac{\Delta }{{4a}}} \right),\,\,\,\Delta = {b^2} - 4ac\).
- Trục đối xứng là đường thẳng \(x = - \dfrac{b}{{2a}}\).
- Bề lõm hướng lên trên khi \(a > 0\) và hướng xuống dưới khi \(a < 0\)
- Cách vẽ:
+) Xác định đỉnh \(\left( { - \dfrac{b}{{2a}}; - \dfrac{\Delta }{{4a}}} \right)\).
+) Xác định trục đối xứng và hướng bề lõm của parabol.
+) Xác định một số điểm cụ thể của parabol (chẳng hạn giao điểm của parabol với các trục tọa độ và các điểm đối xứng với chúng qua trục đối xứng).
+) Căn cứ vào tính đối xứng, bề lõm và hình dáng parabol để “nối” các điểm đó lại.
