I. Hàm số và đồ thị
1. Hàm số
Định nghĩa
Nếu với mỗi giá trị của x thuộc tập hợp số D có một và chỉ một giá trị tương ứng của y thuộc tập
số thực R thì ta có một hàm số.
Kí hiệu: y=f(x).
Ta gọi x là biến số và y là hàm số của x.
Tập hợp D gọi là tập xác định của hàm số.
Tập tất cả các giá trị y nhận được, gọi là tập giá trị của hàm số.
2. Đồ thị của hàm số
Đồ thị của hàm số y=f(x) xác định trên tập D là tập hợp tất cả các điểm M(x;f(x)) trên mặt phẳng toạ độ với mọi x∈D.
3. Sự biến thiên
Cho hàm số y=f(x) xác định trên khoảng (a;b).
- Hàm số y=f(x) đồng biến (tăng) trên (a;b) nếu:
∀x1,x2∈K:x1<x2⇒f(x1)<f(x2)
- Hàm số y=f(x) nghịch biến (giảm) trên (a;b) nếu:∀x1,x2∈K:x1<x2⇒f(x1)>f(x2)
II. Hàm số bậc hai. Đồ thị hàm số bậc hai và ứng dụng
1. Hàm số bậc hai
Định nghĩa
- Hàm số bậc hai là hàm số được cho bằng biểu thức có dạng y=ax2+bx+c(a≠0).
Trong đó x là biến số, a, b, c là các hằng số.
- TXĐ: D=R.
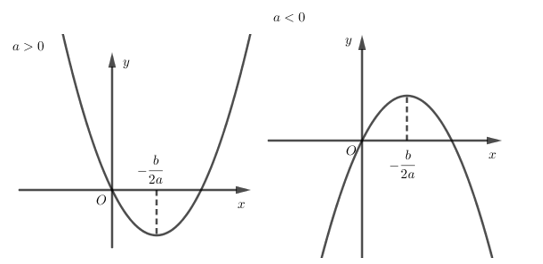
2. Đồ thị hàm số bậc hai
- Có dáng là đường Parabol có đỉnh (−b2a;−Δ4a),Δ=b2−4ac.
- Trục đối xứng là đường thẳng x=−b2a.
- Bề lõm hướng lên trên khi a>0 và hướng xuống dưới khi a<0
- Cách vẽ:
+) Xác định đỉnh (−b2a;−Δ4a).
+) Xác định trục đối xứng và hướng bề lõm của parabol.
+) Xác định một số điểm cụ thể của parabol (chẳng hạn giao điểm của parabol với các trục tọa độ và các điểm đối xứng với chúng qua trục đối xứng).
+) Căn cứ vào tính đối xứng, bề lõm và hình dáng parabol để “nối” các điểm đó lại.
III. Dấu của tam thức bậc hai
1. Tam thức bậc hai
Tam thức bậc hai (đối với x) là biểu thức dạng ax2+bx+c. Trong đó a,b,c là những số cho trước với a≠0.
Nghiệm của phương trình ax2+bx+c=0 được gọi là nghiệm của tam thức bậc hai f(x)=ax2+bx+c; Δ=b2−4ac và Δ′=b′2−ac theo thứ tự được gọi là biệt thức và biệt thức thu gọn của tam thức bậc hai f(x)=ax2+bx+c.
2. Dấu của tam thức bậc hai
Dấu của tam thức bậc hai được thể hiện trong bảng sau

Chú ý: Khi xét dấu tam thức bậc hai mà có hai nghiệm phân biệt, các em có thể nhớ theo quy tắc “Trong trái ngoài cùng”, nghĩa là trong khoảng hai nghiệm thì trái dấu với a, ngoài khoảng hai nghiệm thì cùng dấu với a.
Nhận xét: Cho tam thức bậc hai ax2+bx+c
- ax2+bx+c>0,∀x∈R⇔{a>0Δ<0
- ax2+bx+c≥0,∀x∈R⇔{a>0Δ≤0
- ax2+bx+c<0,∀x∈R⇔{a<0Δ<0
- ax2+bx+c≤0,∀x∈R⇔{a<0Δ≤0
IV. Bất phương trình bậc hai một ẩn
1. Bất phương trình bậc hai
- Bất phương trình bậc hai ẩn x là bất phương trình có dạng ax2+bx+c>0 (hoặc ax2+bx+c≥0,ax2+bx+c<0,ax2+bx+c≤0), trong đó a,b,c là những số thực đã cho và a≠0.
- Số thực x0 gọi là một nghiệm của bất phương trình bậc hai ax2+bx+c>0, nếu ax20+bx0+c>0. Tập hợp gồm tất cả các nghiệm của bất phương trình bậc hai ax2+bx+c>0 gọi là tập nghiệm của bất phương trình này.
2. Giải bất phương trình bậc hai một ẩn
a. Giải bất phương trình bậc hai một ẩn bằng cách xét dấu của tam thức bậc hai
Giải bất phương trình bậc hai f(x)=ax2+bx+c>0 là tìm tập nghiệm của nó, tức là tìm các khoảng mà trong đó f(x) cùng dấu với hệ số a (nếu a>0) hay trái dấu với hệ số a (nếu a<0).
Nhận xét: Để giải bất phương trình bậc hai (một ẩn) có dạng f(x)>0(f(x)=ax2+bx+c), ta chuyển việc giải bất phương trình đó về việc tìm tập hợp những giá trị của x sao cho f(x) mang dấu "+". Cụ thể, ta làm như sau:
Bước 1. Xác định dấu của hệ số a và tìm nghiệm của f(x) (nếu có).
Bước 2. Sử dụng định lí về dấu của tam thức bậc hai để tìm tập hợp những giá trị của x sao cho f(x) mang dấu "+”.
b. Giải bất phương trình bậc hai một ẩn bằng cách sử dụng đồ thị
- Giải bất phương trình bậc hai ax2+bx+c>0 là tìm tập hợp những giá trị của x ứng với phần parabol y=ax2+bx+c nằm phía trên trục hoành.
- Tương tự, giải bất phương trình bậc hai ax2+bx+c<0 là tìm tập hợp những giá trị của x ứng với phần parabol y=ax2+bx+c nằm phía dưới trục hoành.
V. Hai dạng phương trình quy về phương trình bậc hai
a. Giải phương trình chứa căn dạng 1
Để giải phương trình √ax2+bx+c=√dx2+ex+f, ta làm như sau:
Bước 1: Bình phương hai vế của phương trình để được phương trình ax2+bx+c=dx2+ex+f.
Bước 2: Giải phương trình nhận được ở Bước 1 .
Bước 3: Thử lại các giá trị x tìm được ở Bước 2 có thoả mãn phương trình đã cho hay không và kết luận nghiệm.
b. Giải phương trình chứa căn dạng 2
Để giải phương trình √ax2+bx+c=dx+e, ta làm như sau:
Bước 1: Bình phương hai vế của phương trình để được phương trình ax2+bx+c=(dx+e)2.
Bước 2: Giải phương trình nhận được ở Bước 1 .
Bước 3: Thử lại các giá trị x tìm được ở Bước 2 có thoả mãn phương trình đã cho hay không và kết luận nghiệm.

