I. Tính đối xứng của Elip
Ôn tập:
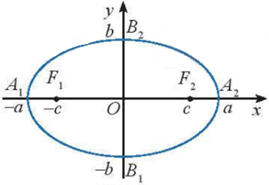
Ta đã biết elip (E) với phương trình chính tắc \(\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1\left( {0 < b < a} \right)\) có các yếu tố:
– Bốn đỉnh là \({A_1}\left( {-a;{\rm{ }}0} \right),{\rm{ }}{A_2}\left( {a,{\rm{ }}0} \right),{\rm{ }}{B_1}\left( {0;{\rm{ }}b} \right),{\rm{ }}{B_2}\left( {0;{\rm{ }}b} \right).\)
– Trục lớn là \({A_1}{A_2}\) có độ dài 2a, trục nhỏ là \({B_1}{B_2}\) có độ dài \(2b\)
— Hai tiêu điểm là\({F_1}\left( { - c;{\rm{ }}0} \right),{\rm{ }}{F_2}(c;\,\,0)\)) với \(c = \sqrt {{a^2} - {b^2}} \)
— Tiêu cự \(2c\) là khoảng cách giữa hai tiêu điểm.
Tính đối xứng:
Elip (E) nhận hai trục toạ độ làm hai trục đối xứng và gốc toạ độ O làm tâm đối xứng. Gốc O còn được gọi là tâm của elip (E).
II. Hình chữ nhật cơ sở của elip

Trong mặt phẳng tọa độ Oxy, cho elip (E) với phương trình chính tắc \(\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1\left( {0 < b < a} \right)\). Khi đó, ta có:
- Hình chữ nhật cơ sở có bốn đỉnh là \[P\left( { - a{\rm{ }};b} \right),{\rm{ }}Q\left( {a{\rm{ }};b} \right),{\rm{ }}R\left( {a{\rm{ }}; - b} \right),{\rm{ }}S\left( { - a; - b} \right).\]
- Bốn đỉnh của elip là trung điểm các cạnh của hình chữ nhật cơ sở.
- Nếu điểm M(x ; y) thuộc (E) thì \(-{\rm{ }}a \le x \le a,\,\,-b \le y \le b\). Do đó, mọi điểm của elip nếu không phải là đỉnh thì đều nằm trong hình chữ nhật cơ sở.
Ví dụ:
Cho elip \(\left( E \right):\dfrac{{{x^2}}}{{25}} + \dfrac{{{y^2}}}{9} = 1\).
a) Tìm tọa độ các đỉnh của elip
b) Tìm tọa độ các đỉnh của hình chữ nhật cơ sở của elip.
Giải
a) Ta có: \({a^2} = 25 \Rightarrow a = 5\); \({b^2} = 9 \Rightarrow b = 3\).
Vậy elip có các đỉnh là \({A_1}\left( { - 5;0} \right),\,{A_2}\left( {5;0} \right),\,{B_1}\left( {0; - 3} \right),{B_2}\left( {0;3} \right)\).
b)Tọa độ các đỉnh của hình chữ nhật cơ sở là:
\(P\left( { - 5;3} \right),Q\left( {5;3} \right),R\left( {5; - 3} \right),S\left( { - 5; - 3} \right)\)
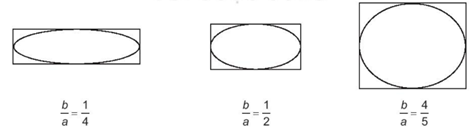
Khi tỉ số \(\dfrac{b}{a}\) càng nhỏ (càng gần về 0), thì hình chữ nhật cơ sở càng “dẹt" và elip càng “gầy".
Khi tỉ số \(\dfrac{b}{a}\) càng lớn (càng gần tới 1), thì hình chữ nhật cơ sở càng gần với hình vuông và elip càng “béo" (càng gần đường tròn)
III. Bán kính qua tiêu của một điểm thuộc elip
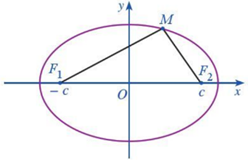
Với mỗi điểm M thuộc đường elip \(\left( E \right)\), các đoạn thẳng \(M{F_1};\,M{F_2}\) được gọi là hai bán kính qua tiêu của điểm M.
Độ dài hai bán kính qua tiêu của điểm M trên elip \(\left( E \right)\):\(\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1\) là \(M{F_1} = {\rm{ }}a + \dfrac{c}{a}x,{\rm{ }}M{F_2} = a - \dfrac{c}{a}x.\)
Chú ý: Vì \( - a \le x \le a\) nên \(a + \dfrac{c}{a}x > 0\) và \(a - \dfrac{c}{a}x > 0\).
Ví dụ:
Tính độ dài hai bán kính qua tiêu của điểm \(M\left( {x;y} \right)\) trên elip \(\left( E \right):\dfrac{{{x^2}}}{{25}} + \dfrac{{{y^2}}}{9} = 1\).
Giải
Ta có: \(a = 5;\,b = 3\, \Rightarrow c = \sqrt {{a^2} - {b^2}} = 4\)
Độ dài hai bán kính qua tiêu của điểm \(M\left( {x;y} \right)\) là:
\(M{F_1} = a + \dfrac{c}{a}x = 5 + \dfrac{4}{5}x;\,M{F_2} = a - \dfrac{c}{a}x = 5 - \dfrac{4}{5}x\)
IV. Tâm sai của elip
Tỉ số giữa tiêu cự và độ dài trục lớn của elip gọi là tâm sai của elip và được kí hiệu là \(e\), tức là \(e = \dfrac{c}{a}\)
Nhận xét:
+ \(0<e<1.\)
+ \(e = \dfrac{{\sqrt {{a^2} - {b^2}} }}{a} = \sqrt {1 - {{\left( {\dfrac{b}{a}} \right)}^2}} \)
Ví dụ: Tìm tọa độ tiêu điểm, tiêu cự và tâm sai của elip có phương trình chính tắc là \(\left( E \right):\dfrac{{{x^2}}}{{25}} + \dfrac{{{y^2}}}{9} = 1\)
Giải
Ta có: \(a = 5,b = 3 \Rightarrow c = \sqrt {{a^2} - {b^2}} = 4\, \Rightarrow 2c = 8\)
Vậy elip có 2 tiêu điểm \({F_1}\left( { - 4;0} \right),\,{F_2}\left( {4;0} \right)\), tiêu cự là 8.
Tâm sai của elip là \(e = \dfrac{c}{a} = \dfrac{4}{5} = 0,8.\)
V. Đường chuẩn của elip
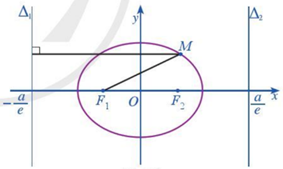
Đường thẳng \({\Delta _1}:x = - \dfrac{a}{e}\) gọi là đường chuẩn ứng với tiêu điểm \({F_1}\left( { - c;0} \right)\)
Đường thẳng \({\Delta _2}:x = \dfrac{a}{e}\) gọi là đường chuẩn ứng với tiêu điểm \({F_2}\left( {c;0} \right)\).
Chú ý:
Tỉ số của khoảng cách từ một điểm M bất kì thuộc đường elip đến tiêu điểm và khoảng cách từ điểm đó đến đường chuẩn tương ứng luôn bằng tâm sai của elip:
\(\dfrac{{M{F_1}}}{{d\left( {M;{\Delta _1}} \right)}} = \dfrac{{M{F_2}}}{{d\left( {M;{\Delta _2}} \right)}} = e\)
Ví dụ: Tìm đường chuẩn của \(\left( E \right):\dfrac{{{x^2}}}{{25}} + \dfrac{{{y^2}}}{9} = 1\)
Giải
Ta có: \(a = 5,b = 3 \Rightarrow c = \sqrt {{a^2} - {b^2}} = 4\, \Rightarrow 2c = 8\)
Vậy elip có 2 tiêu điểm \({F_1}\left( { - 4;0} \right),\,{F_2}\left( {4;0} \right)\), tiêu cự là 8.
Tâm sai của elip là \(e = \dfrac{c}{a} = \dfrac{4}{5} = 0,8.\)
Đường chuẩn ứng với tiêu điểm \({F_1}\left( { - 4;0} \right)\) là \({\Delta _1}:x = - \dfrac{{25}}{4}\)
Đường chuẩn ứng với tiêu điểm \({F_2}\left( {4;0} \right)\) là \({\Delta _1}:x = \dfrac{{25}}{4}\)
VI. Liên hệ giữa đường tròn và đường elip
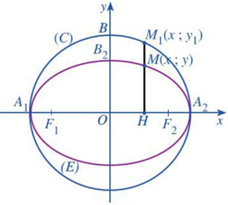
- Mỗi điểm \({M_1}\left( {x;{y_1}} \right)\) trên đường tròn (C) qua “phép co” theo trục tung với hệ số \(\dfrac{a}{b}\) thì biến thành điểm \(M\left( {x;y} \right)\) trên elip (E).
- Mỗi điểm \(M\left( {x;y} \right)\) trên elip (E) qua “phép giãn” theo trục tung với hệ số \(\dfrac{a}{b}\) thì biến thành điểm \({M_1}\left( {x;{y_1}} \right)\) trên đường tròn (C).
VII. Cách vẽ đường elip
Để vẽ elip \(\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1{\rm{ }}\left( {a > b > 0} \right),\) ta có thể làm như sau:
- Vẽ hình chữ nhật cơ sở có bốn cạnh thuộc bốn đường thẳng \(y = b, y = - b, x = a, x = - a.\)
- Xác định bốn đỉnh và một số điểm cụ thể thuộc elip.
- Vẽ đường elip ở phía trong hình chữ nhật cơ sở sao cho elip đó tiếp xúc với các cạnh của hình chữ nhật cơ sở tại bốn đỉnh của nó và đi qua những điểm cụ thể đã chọn.

