I. Sơ đồ tư duy Mệnh đề toán học
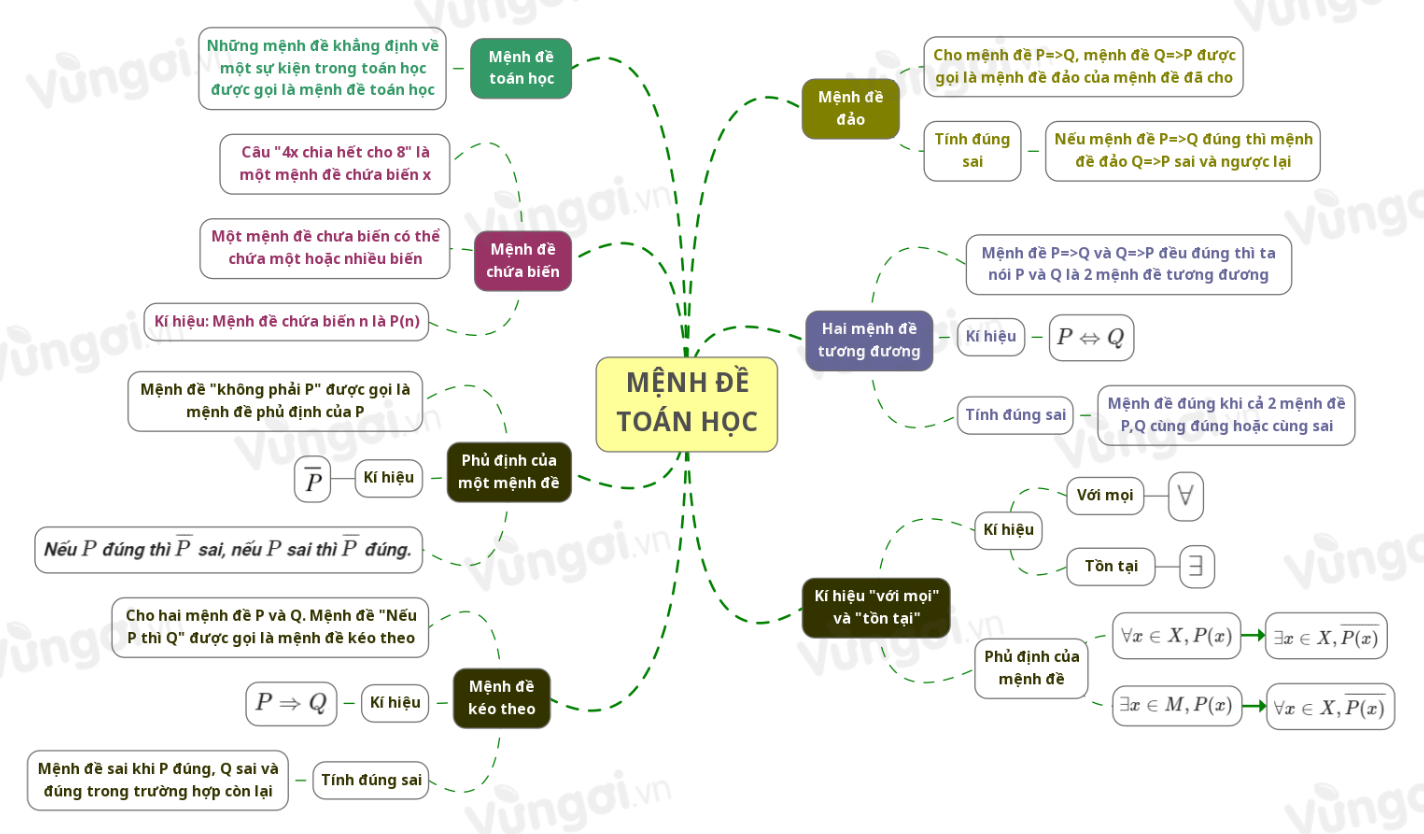
II. Mệnh đề toán học
Những mệnh đề khẳng định về một sự kiện trong toán học được gọi là mệnh đề toán học.
Ví dụ 1:
a) "Số 5 là số nguyên" là một mệnh đề toán học.
b) "Phương trình \({x^2} + 5x - 6 = 0\) có nghiệm nguyên" là một mệnh đề toán học
c) "Đà Nẵng là 1 thành phố của Việt Nam" không phải là một mệnh đề Toán học.
Chú ý:
Mỗi mệnh đề toán học phải hoặc đúng hoặc sai. Một mệnh đề toán học không thể vừa đúng, vừa sai.
Ví dụ 2:
a) "Hình vuông có bốn cạnh" là mệnh đề đúng.
b) "4 là số nguyên tố" là mệnh đề sai vì 4 là hợp số.
III. Mệnh đề chứa biến
Ví dụ 1:
Xét câu “ n chia hết cho 2” với n là số tự nhiên
Ta chưa khẳng định được tính đúng sai của câu này, do đó nó chưa phải là 1 mệnh đề.
Tuy nhiên, nếu thay n bằng số tự nhiên cụ thể thì câu này cho ta một mệnh đề. Chẳng hạn:
+Với \(n = 4\) ta được mệnh đề “4 chia hết cho 2”. Đây là mệnh đề đúng
+ Với \(n = 7\) ta được mệnh đề “7 chia hết cho 2”. Đây là mệnh đề sai.
Ta nói rằng câu “ n chia hết cho 2” là một mệnh đề chứa biến.
Ví dụ 2:
a) Câu “15 chia hết cho 3” là một mệnh đề nhưng không phải là mệnh đề chứa biến
b) Câu “ \(4x\) chia hết cho 8” là một mệnh đề chứa biến \(x\).
Chú ý:
- Một mệnh đề chứa biến có thể chứa một hoặc nhiều biến.
- Ta thường kí hiệu mệnh đề chứa biến \(n\) là \(P\left( n \right)\); mệnh đề chứa biến \(x,y\) là \(P\left( {x,y} \right)\);…
IV. Phủ định của một mệnh đề
Cho mệnh đề \(P\). Mệnh đề “Không phải \(P\)” được gọi là mệnh đề phủ định của \(P\) và kí hiệu là \(\overline P \).
Mệnh đề \(P\) và \(\overline P \) là hai câu khẳng định trái ngược nhau.
Nếu \(P\) đúng thì \(\overline P \) sai, nếu \(P\) sai thì \(\overline P \) đúng.
Mệnh đề phủ định của \(P\) có thể diễn đạt theo nhiều cách khác nhau, miễn là cùng mang một ý nghĩa “không phải \(P\)”.
Ví dụ:
Cho mệnh đề \(P\): “\(6\) chia hết cho \(3\)”. Khi đó, mệnh đề phủ định của \(P\) có thể phát biểu theo 3 cách sau:
Cách 1: \(\overline P \) : “\(6\) không chia hết cho \(3\)”
Cách 2: \(\overline P \) : “\(6\) không là bội của \(3\)”
Cách 3: \(\overline P \) : “\(3\) không là ước của \(6\)”
3 cách trên đều cùng mang một ý nghĩa phủ định của \(P\).
V. Mệnh đề kéo theo
Cho hai mệnh đề \(P\) và \(Q\). Mệnh đề “Nếu \(P\) thì \(Q\)” được gọi là mệnh đề kéo theo.
Kí hiệu: \(P \Rightarrow Q\).
Tính đúng sai: Mệnh đề \(P \Rightarrow Q\) chỉ sai khi \(P\) đúng, \(Q\) sai và đúng trong các trường hợp còn lại.
Ví dụ:
a) Mệnh đề “Nếu \(3\) là số nguyên tố thì \(3\) chia hết cho \(3\)” là mệnh đề đúng vì hai mệnh đề “\(3\) là số nguyên tố” và “\(3\) chia hết cho \(3\)” đều đúng.
b) Mệnh đề “Nếu \(3\) không là số nguyên tố thì \(3\) không chia hết cho \(3\)” là mệnh đề đúng vì hai mệnh đề “\(3\) không là số nguyên tố” và “\(3\) không chia hết cho \(3\)” đều sai.
c) Mệnh đề “Nếu \(3\) không là số nguyên tố thì \(3\) chia hết cho \(3\)” là mệnh đề đúng vì mệnh đề “\(3\) không là số nguyên tố” sai và “\(3\) chia hết cho \(3\)” đúng.
d) Mệnh đề “Nếu \(3\) là số nguyên tố thì \(3\) không chia hết cho \(3\)” là mệnh đề sai vì mệnh đề “\(3\) là số nguyên tố” đúng và “\(3\) không chia hết cho \(3\)” sai.
Nhận xét:
Mệnh đề \(P \Rightarrow Q\) còn được phát biểu là “P kéo theo Q” hoặc “Từ P suy ra Q”
Khi mệnh đề \(P \Rightarrow Q\) là định lí, ta nói:
P là giả thiết, Q là kết luận của định lí;
P là điều kiện đủ để có Q;
Q là điều kiện cần để có P.
VI. Mệnh đề đảo
Cho mệnh đề kéo theo \(P \Rightarrow Q\). Mệnh đề \(Q \Rightarrow P\) được gọi là mệnh đề đảo của mệnh đề \(P \Rightarrow Q\).
Tính đúng sai: Nếu mệnh đề ban đầu \(P \Rightarrow Q\) đúng thì mệnh đề đảo \(Q \Rightarrow P\) sai và ngược lại.
Chú ý: Mệnh đề đảo của một mệnh đề đúng không nhất thiết là đúng
Ví dụ:
Mệnh đề “Nếu $ABC$ là tam giác vuông cân thì $ABC$ là tam giác vuông” có mệnh đề đảo là “Nếu $ABC$ là tam giác vuông thì $ABC$ là tam giác vuông cân”.
VII. Hai mệnh đề tương đương
Mệnh đề \(P \Rightarrow Q\) và \(Q \Rightarrow P\) đều đúng thì ta nói P và Q là hai mệnh đề tương đương.
Kí hiệu: \(P \Leftrightarrow Q\).
Tính đúng sai:
Mệnh đề \(P \Leftrightarrow Q\) chỉ đúng khi cả hai mệnh đề \(P \Rightarrow Q\) và \(Q \Rightarrow P\) đều đúng, hay nói cách khác: \(P \Leftrightarrow Q\) chỉ đúng khi cả hai mệnh đề $P,Q$ cùng đúng hoặc cùng sai.
Ví dụ:
Cho các mệnh đề: \(P\): “Tứ giác $ABCD$ là hình chữ nhật có hai cạnh kề bằng nhau”.
\(Q\): “Tứ giác $ABCD$ là hình vuông”.
Mệnh đề \(P \Leftrightarrow Q\): “Tứ giác $ABCD$ là hình chữ nhật có hai cạnh kề bằng nhau nếu và chỉ nếu tứ giác $ABCD$ là hình vuông” là mệnh đề đúng vì các mệnh đề:
+) \(P \Rightarrow Q\): “Nếu tứ giác $ABCD$ là hình chữ nhật có hai cạnh kề bằng nhau thì tứ giác $ABCD$ là hình vuông” là mệnh đề đúng.
+) \(Q \Rightarrow P\): “Nếu tứ giác $ABCD$ là hình vuông thì tứ giác $ABCD$ là hình chữ nhật có hai cạnh kề bằng nhau” là mệnh đề đúng.
VIII. Kí hiệu "với mọi" và "tồn tại"
Trong toán học, để ngắn gọn, người ta dùng các kí hiệu \(\forall \) (đọc là với mọi) và \(\exists \) (đọc là tồn tại) để phát biểu những mệnh đề.
Tính đúng sai:
Mệnh đề " \(\forall x \in M,P(x)\) " đúng nếu với mọi \({x_0} \in M,P\left( {{x_0}} \right)\) là mệnh đề đúng.
Mệnh đề "\(\exists x \in M,P(x)\) " đúng nếu có \({x_0} \in M\) sao cho \(P\left( {{x_0}} \right)\) là mệnh đề đúng.
Chú ý:
Cho mệnh đề " \(P(x),x \in X\) ".
- Phủ định của mệnh đề " \(\forall x \in X,P(x)\) " là mệnh đề " \(\exists x \in X,\overline {P(x)} \) ".
- Phủ định của mệnh đề " \(\exists x \in X,P(x)\) " là mệnh đề " \(\forall x \in X,\overline {P(x)} \) ".
Ví dụ: Cho mệnh đề chứa biến \(Q\left( n \right)\): “\({2^n} - 1\) là số nguyên tố”.
+) Mệnh đề “\(\forall n \in {N^*},Q\left( n \right)\)” phát biểu là: Với mọi \(n\) là số nguyên dương ta đều có \({2^n} - 1\) là số nguyên tố.
Đây là mệnh đề sai vì với \(n = 4\) thì \({2^4} - 1 = 15\) không là số nguyên tố.
+) Mệnh đề phủ định của mệnh đề “\(\forall n \in {N^*},Q\left( n \right)\)” là “\(\exists n \in {N^*},\overline {Q\left( n \right)} \)”, phát biểu là: Tồn tại số nguyên dương \(n\) để \({2^n} - 1\) không là số nguyên tố.
Đây là mệnh đề đúng vì với \(n = 4\) thì \({2^4} - 1 = 15\) không là số nguyên tố.
+) Mệnh đề “\(\exists \in {N^*},Q\left( n \right)\)” phát biểu là: Tồn tại \(n\) là số nguyên dương để \({2^n} - 1\) là số nguyên tố.
Đây là mệnh đề đúng vì với \(n = 3\) thì \({2^3} - 1 = 7\) là số nguyên tố.
+) Mệnh đề phủ định của mệnh đề “\(\exists n \in {N^*},Q\left( n \right)\)” là “\(\forall n \in {N^*},\overline {Q\left( n \right)} \)”, phát biểu là: Với mọi số nguyên dương \(n\) ta đều có \({2^n} - 1\) không là số nguyên tố.
