I. Giá trị lượng giác của một góc từ 0 đến 180
1. Giá trị lượng giác của một góc
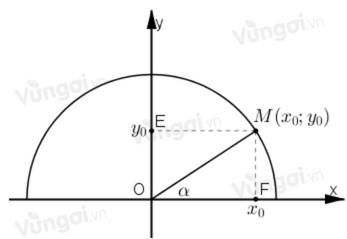
- sin của góc \(\alpha \), kí hiệu là \(\sin \alpha \), được xác định bởi: \(\sin \alpha = {y_0}\);
- côsin của góc \(\alpha \), kí hiệu là \(\cos \alpha \), được xác định bởi: \(\cos \alpha = {x_0}\);
- tang của góc \(\alpha \), kí hiệu là tan \(\alpha \), được xác định bởi: \(\tan \alpha = \dfrac{{{y_0}}}{{{x_0}}}\left( {{x_0} \ne 0} \right)\);
- côtang của góc \(\alpha \), kí hiệu là \(\cot \alpha \), được xác định bởi: \(\cot \alpha = \dfrac{{{x_0}}}{{{y_0}}}\left( {{y_0} \ne 0} \right)\).
Các số \(\sin \alpha ,\cos \alpha ,\tan \alpha ,\cot \alpha \) được gọi là các giá trị lượng giác của góc \(\alpha \).
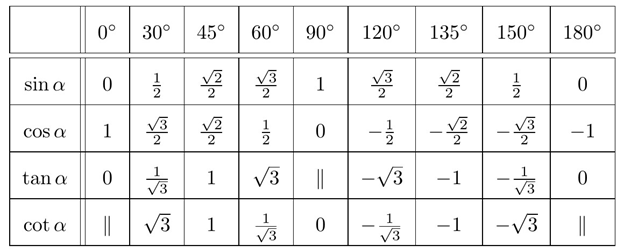
Bảng giá trị lượng giác của một số góc đặc biệt:
2. Mối quan hệ giữa các giá trị lượng giác của hai góc bù nhau
Đối với hai góc bù nhau, \(\alpha \) và \({180^\circ } - \alpha \), ta có:
- \(\sin \left( {{{180}^\circ } - \alpha } \right) = \sin \alpha \);
- \(\cos \left( {{{180}^\circ } - \alpha } \right) = - \cos \alpha \);
- \(\tan \left( {{{180}^\circ } - \alpha } \right) = - \tan \alpha \left( {\alpha \ne {{90}^\circ }} \right)\)
- \(\cot \left( {{{180}^\circ } - \alpha } \right) = - \cot \alpha \left( {{0^\circ } < \alpha < {{180}^\circ }} \right)\).
3. Sử dụng MTCT để tính giá trị lượng giác của một góc
- Để tính các giá trị lượng giác bằng MTCT, sau khi đưa máy về chế độ “độ” ta làm như sau:
- Tính góc khi biết một giá trị lượng giác của góc đó:
II. Định lí côsin và định lí sin trong tam giác
1. Định lí côsin
Cho tam giác $A B C$ có \(BC = a,CA = b,AB = c\). Khi đó:
\(\begin{array}{l}{a^2} = {b^2} + {c^2} - 2bc\cos A\\{b^2} = {c^2} + {a^2} - 2ca\cos B\\{c^2} = {a^2} + {b^2} - 2ab\cos C\end{array}\)
Hệ quả
\(\begin{array}{l}\cos A = \dfrac{{{b^2} + {c^2} - {a^2}}}{{2bc}}\\\cos B = \dfrac{{{c^2} + {a^2} - {b^2}}}{{2ca}}\\\cos C = \dfrac{{{a^2} + {b^2} - {c^2}}}{{2ab}}\end{array}\)
2. Định lí sin
Cho tam giác \(ABC\) có \(BC = a,CA = b,AB = c\) và bán kính đường tròn ngoại tiếp là R. Khi đó:
\(\dfrac{a}{{\sin A}} = \dfrac{b}{{\sin B}} = \dfrac{c}{{\sin C}} = 2R\)
Hệ quả:
\(a = 2R\sin A\)
\(b = 2R\sin B\)
\(c = 2R\sin C\)
III. Giải tam giác
1. Tính các cạnh và góc của tam giác dựa trên một số điều kiện cho trước
Như ta đã biết, một tam giác hoàn toàn xác định nếu biết một trong những dữ kiện sau:
- Biết độ dài hai cạnh và độ lớn góc xen giữa hai cạnh đó;
- Biết độ dài ba cạnh;
- Biết độ dài một cạnh và độ lớn hai góc kề với cạnh đó.
2. Tính diện tích tam giác
Cho tam giác $ABC$. Ta kí hiệu:
- \({h_a},{h_b},{h_c}\) là độ dài các đường cao lần lượt ứng với các cạnh $BC, CA, AB$.
- $R$ là bán kính đường tròn ngoại tiếp tam giác.
- $r$ là bán kính đường tròn nội tiếp tam giác.
- $p$ là nửa chu vi tam giác.
- S là diện tích tam giác.
Ta có các công thức tính diện tích tam giác sau:
1) \(S = \dfrac{1}{2}a{h_a} = \dfrac{1}{2}b{h_b} = \dfrac{1}{2}c{h_c}\);
2) \(S = \dfrac{1}{2}ab\sin C = \dfrac{1}{2}bc\sin A = \dfrac{1}{2}ac\sin B\);
3) \(S = \dfrac{{abc}}{{4R}}\);
4) \(S = pr\);
5) \(S = \sqrt {p(p - a)(p - b)(p - c)} \) (công thức Heron).
IV. Khái niệm vectơ
1. Khái niệm vectơ
- Vectơ là một đoạn thẳng có hướng, nghĩa là, trong hai điểm mút của đoạn thẳng, đã chỉ rõ điểm đầu, điểm cuối.
- Độ dài của vectơ là khoảng cách giữa điểm đầu và điểm cuối của vectơ đó.
Vectơ có điểm đầu là A, điểm cuối là B ta kí hiệu : \(\overrightarrow {AB} \)
Vectơ còn được kí hiệu là: \(\overrightarrow a ,{\rm{ }}\overrightarrow b ,{\rm{ }}\overrightarrow x ,{\rm{ }}\overrightarrow y ,...\)
- Độ dài đoạn thẳng \(AB\) gọi là độ dài vectơ \(\overrightarrow {AB} \), kí hiệu \(\left| {\overrightarrow {AB} } \right|\). Vậy \(\left| {\overrightarrow {AB} } \right| = AB\).
2. Vectơ cùng phương, vectơ cùng hướng
Đường thẳng đi qua điểm đầu và điểm cuối của vectơ gọi là giá của vectơ
Hai vectơ có giá song song hoặc trùng nhau gọi là hai vectơ cùng phương
3. Hai vectơ bằng nhau
- Hai vectơ bằng nhau nếu chúng cùng hướng và cùng độ dài.
Nhận xét: Khi cho trước vectơ \(\vec a\) và điểm \(O\), thì ta luôn tìm được một điểm \(A\) duy nhất sao cho \(\overrightarrow {OA} = \vec a\).
Vectơ đối của vectơ \(\overrightarrow a \) là vectơ ngược hướng và có cùng độ dài với vectơ \(\overrightarrow a \)
Kí hiệu: \( - \overrightarrow a \)
Như vậy \(\overrightarrow a + \left( { - \overrightarrow a } \right) = \overrightarrow 0 {\rm{, }}\forall \overrightarrow a \) và \(\overrightarrow {AB} = - \overrightarrow {BA} \)
4. Vectơ-không
Vectơ – không là vectơ có điểm đầu trùng điểm cuối. Kí hiệu là \(\overrightarrow 0 \)
V. Tổng và hiệu của hai vectơ
1.Tổng của hai vectơ
a. Định nghĩa:
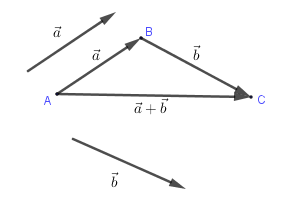
Cho hai vectơ \(\overrightarrow a \,;\,\,\overrightarrow b \). Từ điểm A tùy ý vẽ \(\overrightarrow {AB} = \overrightarrow a \) rồi từ B vẽ \(\overrightarrow {BC} = \overrightarrow b \).
Khi đó vectơ \(\overrightarrow {AC} \) được gọi là tổng của hai vectơ \(\overrightarrow a \,;\,\,\overrightarrow b \).
Kí hiệu \(\overrightarrow {AC} = \overrightarrow a + \overrightarrow b \)
b. Tính chất :
+ Giao hoán : \(\overrightarrow a + \overrightarrow b = \overrightarrow b + \overrightarrow a \)
+ Kết hợp : \(\left( {\overrightarrow a + \overrightarrow b } \right) + \overrightarrow c = \overrightarrow a + \left( {\overrightarrow b + \overrightarrow c } \right)\)
+ Tính chất vectơ – không: \(\overrightarrow a + \overrightarrow 0 = \overrightarrow a {\rm{, }}\forall \overrightarrow a \)
c. Các quy tắc:
Quy tắc ba điểm : Cho \(A,B,C\) tùy ý, ta có : \(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)
Quy tắc hình bình hành : Nếu \(ABCD\) là hình bình hành thì \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \)
2. Hiệu của hai vectơ
Hiệu của hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) là tổng của vectơ \(\overrightarrow a \) và vectơ đối của vectơ \(\overrightarrow b \).
Kí hiệu là \(\overrightarrow a - \overrightarrow b = \overrightarrow a + \left( { - \overrightarrow b } \right)\)
Chú ý:
Quy tắc về hiệu vectơ: Cho \(O,A,B\) tùy ý ta có: \(\overrightarrow {OB} - \overrightarrow {OA} = \overrightarrow {AB} \)
VI. Tích của một số với một vectơ
1. Định nghĩa tích của một vectơ với một số
Tích của vectơ \(\overrightarrow a \) với số thực \(k \ne 0\) là một vectơ, kí hiệu là \(k\overrightarrow a \), cùng hướng với \(\overrightarrow a \) nếu \(k > 0\), ngược hướng với \(\overrightarrow a \) nếu \(k < 0\) và có độ dài bằng \(\left| k \right|\left| {\overrightarrow a } \right|\)
Quy ước: \(0\overrightarrow a = \overrightarrow 0 \) và \(k\overrightarrow 0 = \overrightarrow 0 \)
2. Tính chất của phép nhân vectơ với một số
Với hai vectơ \(\vec a\) và \(\vec b\) bất kì, với mọi số thực \(k\) và \(m\), ta có:
\(\begin{array}{l}{\rm{i}}){\rm{ }}(k + m)\overrightarrow a = k\overrightarrow a + m\overrightarrow a {\rm{ }}\\{\rm{ii}}){\rm{ }}k(\overrightarrow a \pm \overrightarrow b ) = k\overrightarrow a \pm k\overrightarrow b {\rm{ }}\,\,\,\,\,\,\,{\rm{ }}\\{\rm{iii}})\,\,k(m\overrightarrow a ) = (km)\overrightarrow a {\rm{ }}\,\,\,\,\,\,\,\,\,\,{\rm{ }}\\{\rm{iv}})\,\,\,k\overrightarrow a = \overrightarrow 0 \Leftrightarrow \left[ \begin{array}{l}k = 0\\\overrightarrow a = \overrightarrow 0 \end{array} \right.\\{\rm{v) 1}}\overrightarrow a = \overrightarrow a ;\,\,\,( - {\rm{1)}}\overrightarrow a = - \overrightarrow a \,\,\,\,\,\,\,\,\,\,\,\,\end{array}\)
3. Một số ứng dụng tích của một vectơ với một số
a. Trung điểm của đoạn thẳng
Cho \(I\) là trung điểm \(AB\) và một điểm \(M\) bất kì, khi đó:
+) \(\overrightarrow {IA} + \overrightarrow {IB} = \overrightarrow 0 \).
+) \(\overrightarrow {MA} + \overrightarrow {MB} = 2\overrightarrow {MI} \).
b. Trọng tâm của tam giác
Cho \(G\) là trọng tâm tam giác \(ABC\) và \(M\) là một điểm bất kì, khi đó:
+) \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \).
+) \(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = 3\overrightarrow {MG} \).
c. Điều kiện để hai vectơ cùng phương. Điều kiện để ba điểm thẳng hàng
Điều kiện cần và đủ để hai vectơ \(\vec a\) và \(\vec b(\vec b \ne \vec 0)\) cùng phương là có một số thực \(k\) để \(\vec a = k\vec b\).
Điều kiện cần và đủ để ba điểm phân biệt $A, B, C$ thẳng hàng là có số thực \(k\) để \(\overrightarrow {AB} = k\overrightarrow {AC} .\)
Chú ý: Cho hai vectơ \(\vec a\) và \(\vec b\) không cùng phương. Với mọi vectơ \(\vec c\) luôn tồn tại duy nhất cặp số thực \((m;n)\) sao cho \(\vec c = m\vec a + n\vec b\).
d. Phương pháp phân tích một véctơ qua hai véctơ không cùng phương:
Sử dụng các quy tắc ba điểm (xen thêm điểm vào giữa để làm xuất hiện các véctơ không cùng phương đề bài yêu cầu), các tính chất trung điểm, trọng tâm, tích của một véctơ với một số để biến đổi làm sao cho xuất hiện.
Chú ý: Cho đoạn thẳng \(AB\), một điểm \(I \in AB\) thỏa mãn \(\overrightarrow {IA} = k\overrightarrow {IB} \) thì với điểm \(M\) bất kì ta luôn có:
\(\overrightarrow {MI} = \dfrac{{ - 1}}{{k - 1}}\overrightarrow {MA} + \dfrac{k}{{k - 1}}\overrightarrow {MB} \)
VII. Tích vô hướng của hai vectơ
1. Góc giữa hai vectơ
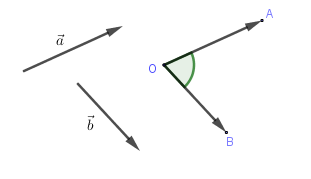
Cho hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) đều khác \(\overrightarrow 0 \). Từ một điểm \(O\) bất kì ta vẽ \(\overrightarrow {OA} = \overrightarrow a ;\,\,\overrightarrow {OB} = \overrightarrow b \)
Khi đó, số đo của góc AOB được gọi là số đo góc giữa hai véc tơ \(\overrightarrow a ,\overrightarrow b \)
Kí hiệu: \(\left( {\overrightarrow a ;\overrightarrow b } \right) = \left( {\overrightarrow {OA} ,\overrightarrow {OB} } \right) = \widehat {AOB}\).
+ Quy ước : Nếu \(\overrightarrow a = \overrightarrow 0 \) hoặc \(\overrightarrow b = \overrightarrow 0 \) thì ta xem góc giữa hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) là tùy ý (từ \({0^0}\) đến \({180^0}\)).
2. Tích vô hướng của hai vectơ
Tích vô hướng của hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) là một số, kí hiệu là \(\overrightarrow a .\overrightarrow b \), được xác định bởi công thức: \(\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|\left| {\overrightarrow b } \right|.\cos \left( {\overrightarrow a ,\overrightarrow b } \right)\).
3. Tính chất tích vô hướng của hai vectơ
Với ba vectơ bất kì \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) và mọi số thực k ta luôn có:
\(\begin{array}{l}1){\rm{ }}\overrightarrow a .\overrightarrow b = \overrightarrow b .\overrightarrow a \\2){\rm{ }}\overrightarrow a (\overrightarrow b \pm \overrightarrow c ) = \overrightarrow a .\overrightarrow b \pm \overrightarrow a .\overrightarrow c \\3){\rm{ }}(k\overrightarrow a )\overrightarrow b = k(\overrightarrow a .\overrightarrow b ) = \overrightarrow a (k\overrightarrow b )\\4){\rm{ }}{\overrightarrow a ^2} \ge 0,{\overrightarrow a ^2} = 0 \Leftrightarrow \overrightarrow a = \overrightarrow 0 \end{array}\)
4. Một số ứng dụng tích vô hướng của hai vectơ
a. Tính độ dài của đoạn thẳng
Với hai điểm $A, B$ phân biệt, ta có: \({\overrightarrow {AB} ^2} = |\overrightarrow {AB} {|^2}\).
Do đó độ dài đoạn thẳng $A B$ được tính như sau: \(AB = \sqrt {{{\overrightarrow {AB} }^2}} \).
b. Chứng minh hai đường thẳng vuông góc
- Hai đường thẳng \(AB\) và \(CD\) vuông góc với nhau khi và chỉ khi \(\overrightarrow {AB} \cdot \overrightarrow {CD} = 0\).
- Cũng như vậy, hai đường đường thẳng \(a\) và \(b\) vuông góc khi và chỉ khi \(\vec u \cdot \vec v = 0\), trong đó \(\vec u \ne \vec 0,\vec v \ne \vec 0\), giá của vectơ \(\vec u\) song song hoặc trùng với đường thẳng \(a\) và giá của vectơ \(\vec v\) song song hoặc trùng với đường thẳng \(b\).
