I. Công thức nhị thức Newton
Với mỗi số tự nhiên n, ta có:
(a+b)n=C0nan+C1nan−1b+…+Cknan−kbk+…+Cn−1nabn−1+Cnnbn.
Công thức (1) được gọi là công thức nhị thức Newton, gọi tắt là nhị thức Newton.
Chú ý:
a) Trong cách viết vế phải của (1), số hạng Cknan−kbk(0≤k≤n) được gọi là số hạng tổng quát.
b) Vế phải của (1) gồm n+1 số hạng. Đi qua các số hạng từ trái sang phải, số mũ của a giảm dần, số mũ của b tăng dần, nhưng tổng của chúng không đổi và bằng n (quy ước a0=b0=1).
Ví dụ:
(x+2)6=C06.x6+C16.x5.2+C26.x4.22+C36.x3.23+C46.x2.24+C56.x.25+C66.26=x6+12x5+60x4+160x3+240x2+192x+64.
Số hạng chứa xk trong khai triển của (ax+b)n là Cn−kn(ax)kbn−k hay Cn−knakbn−kxk
Do đó, hệ số của x trong khai triển của (ax+b)n là Cn−knakbn−k
II. Tam giác Pascal
Trong khai triển của (a+b)n (với n=1,2,3,4,5):
1. Có n+1 số hạng, số hạng đầu tiên là an và số hạng cuối cùng là bn.
2. Tổng số mũ của a và b trong mỗi số hạng đều bằng n.
3. Số mũ của a giảm 1 đơn vị và số mũ của b tăng 1 đơn vị khi chuyển từ số hạng này đến số hạng tiếp theo, tính từ trái sang phải.
Nhận xét:
Xuất phát từ dãy các hệ số trong khai triển nhị thức Newton (a+b)n với n∈N, ta bổ sung thêm hai dòng đầu tiên và nhận được tam giác các hệ số như sau:
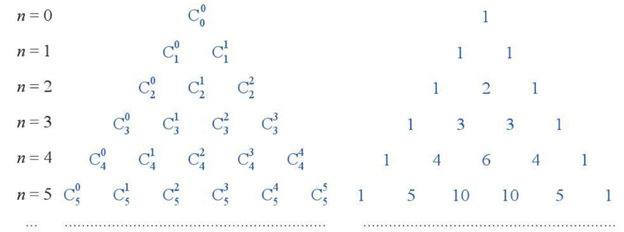
Tam giác số ở trên được gọi là tam giác Pascal
Tính chất của các số Ckn:
+Ckn=Cn−kn(0≤k≤n)(Tính chất đối xứng)
+ Ck−1n−1+Ckn−1=Ckn(1≤k≤n)(Hệ thức Pascal)
III. Vận dụng công thức nhị thức Newton
Công thức nhị thức Newton với các dạng mở rộng của nó có nhiều ứng dụng quan trọng
trong toán học. Dưới đây, ta xét thêm vài ví dụ đơn giản
Ví dụ 1:
Xác định hệ số của x4y6 trong khai triển (2x−y)10.
Giải
Theo công thức nhị thức Newton, ta có:
(2x−y)10=C010(2x)10+C110(2x)9(−y)+...+Ck10(2x)10−k(−y)k+...+C1010(−y)10=210C010x10−29C110x9y+...+(−1)k210−kCk10x10−kyk+...+C1010y10
Số hạng chứa x4y6 ứng với giá trị k=6. Do đó, hệ số của x4y6 là
(−1)6.24.C610=16.210=3360.
Ví dụ 2:
Chứng minh rằng đẳng thức sau đây đúng với mọi n∈N∗:
C0n+C1n+C2n+...+Cnn=2n.
Giải
Theo công thức nhị thức Newton, ta có
(x+1)n=C0nxn+C1nxn−1+C2nxn−2+...+Cn−1nx+Cnn.
Thay x=1 vào công thức trên, ta nhận được
C0n+C1n+C2n+...+Cnn=2n.
Đây là điều phải chứng minh.

