I. Tọa độ của một điểm
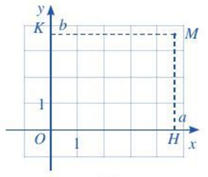
Để xác định toạ độ của một điểm \(M\) tuỳ ý trong mặt phẳng toạ độ $Oxy$, ta làm như sau:
- Từ \(M\) kẻ đường thẳng vuông góc với trục hoành và cắt trục hoành tại điểm \(H\) ứng với số \(a\). Số \(a\) là hoành độ của điểm \(M\).
- Từ \(M\) kẻ đường thẳng vuông góc với trục tung và cắt trục tung tại điểm \(K\) ứng với số \(b\). Số \(b\) là tung độ của điểm \(M\).
Cặp số \((a;b)\) là toạ độ của điểm \(M\) trong mặt phẳng toạ độ $Oxy$.
Ta kí hiệu là \(M(a;b)\).
II. Tọa độ của một vectơ
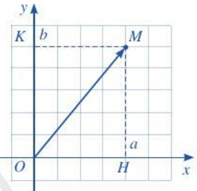
Tọa độ của điểm \(M\) được gọi là tọa độ của vectơ \(\overrightarrow {OM} \).
Nếu \(\overrightarrow {OM} \) có toạ độ \((a;b)\) thì ta viết \(\overrightarrow {OM} = (a;b)\).
Chú ý:
Trong mặt phẳng toạ độ $Oxy$ ta có \(\overrightarrow {OM} = (a;b) \Leftrightarrow M(a;b)\)
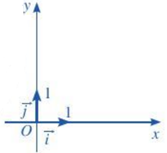
- Vectơ \(\vec i\) có điểm gốc là \(O\) và có toạ độ \((1;0)\) gọi là vectơ đơn vị trên trục Ox.
- Vectơ \(\vec j\) có điểm gốc là \(O\) và có toạ độ \((0;1)\) gọi là vectơ đơn vị trên trục Oy
Định lí:
Trong mặt phẳng toạ độ $Oxy$, nếu \(\vec u = (a;b)\) thì \(\vec u = a\vec i + b\vec j\). Ngược lại, nếu \(\vec u = a\vec i + b\vec j\) thì \(\vec u = (a;b)\).
Ví dụ: \(\overrightarrow a = \left( { - 1;4} \right)\) thì \(\overrightarrow a = - \overrightarrow i + 4\overrightarrow j \)
Chú ý:
Với \(\vec a = \left( {{x_1};{y_1}} \right)\) và \(\vec b = \left( {{x_2};{y_2}} \right)\), ta có: \(\vec a = \vec b \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{x_1} = {x_2}}\\{{y_1} = {y_2}}\end{array}} \right.\).
III. Liên hệ giữa tọa độ của điểm và tọa độ của vectơ
Trong mặt phẳng toạ độ $O x y$, cho hai điểm \(A\left( {{x_A};{y_A}} \right)\) và \(B\left( {{x_B};{y_B}} \right)\).
Ta có: \(\overrightarrow {AB} = \left( {{x_B} - {x_A};{y_B} - {y_A}} \right)\).
Ví dụ:
Trong mặt phẳng tọa độ, cho hai điểm \(A\left( {1;4} \right);\,B\left( {2; - 5} \right)\) thì tọa độ của vectơ \(\overrightarrow {AB} = \left( {2 - 1; - 5 - 4} \right) = \left( {1; - 9} \right)\).
