I. Tính đối xứng của hypebol
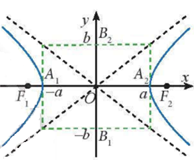
Trong mặt phẳng Oxy,xét hypebol có phương trình chính tắc \(\dfrac{{{x^2}}}{{{a^2}}} - \dfrac{{{y^2}}}{{{b^2}}} = 1\left( {a > 0;b > 0} \right)\):
- Cắt trục Ox tại hai đỉnh \({A_1}\left( { - a;0} \right),{A_2}\left( {a;0} \right)\) nhưng không cắt trục Oy
- Trục thực là \({A_1}{A_2}\) có độ dài \(2a\).
- Trục ảo là \({B_1}{B_2}\) có độ dài \(2b\) với \({B_1}\left( {0; - b} \right),{B_2}\left( {0;b} \right)\) là 2 điểm trên Oy.
- Hai tiêu điểm \({F_1}\left( { - c;0} \right),{F_2}\left( {c;0} \right)\) với \(c = \sqrt {{a^2} + {b^2}} \).
- Tiêu cự \(2c\) là khoảng cách giữa 2 tiêu điểm.
Chú ý: Nếu điểm \(M\left( {x;y} \right)\) nằm trên hypebol (H) thì các điểm \({M_1}\left( {x; - y} \right),{M_2}\left( { - x;y} \right),{M_3}\left( { - x; - y} \right)\) cũng nằm trên hypebol (H).
Hypebol (H) nhận hai trục tọa độ làm hai trục đối xứng và gốc tọa độ O làm tâm đối xứng. Gốc O còn được gọi là tâm của hypebol (H).
II. Hình chữ nhật cơ sở của hypebol
Trong mặt phẳng toạ độ Oxy, cho hypebol (H) có phương trình chính tắc là \(\dfrac{{{x^2}}}{{{a^2}}} - \dfrac{{{y^2}}}{{{b^2}}} = 1\) với \(a > 0,{\rm{ }}b > 0\). Khi đó, ta có:
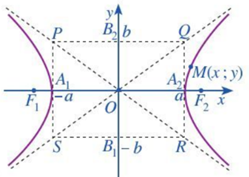
- Hình chữ nhật cơ sở có bốn đỉnh là \(P\left( { - a{\rm{ }};{\rm{ }}b} \right),{\rm{ }}Q\left( {a{\rm{ }};{\rm{ }}b} \right),{\rm{ }}R\left( {a{\rm{ }}; - b} \right),{\rm{ }}S\left( { - a{\rm{ }}; - b} \right).\)
- Mọi điểm của hypebol nếu không phải là đỉnh đều nằm ngoài hình chữ nhật cơ sở của nó.
- Độ dài \(\;{B_1}{B_3} = 2b\) được gọi là độ dài trục ảo của hypebol (H).
- Hai đường thẳng PR và QS lần lượt có phương trình \(y = - \dfrac{b}{a}x,\,y = \dfrac{b}{a}x\) và được gọi là hai đường tiệm cận của hypebol (H).
III. Tâm sai của hypebol
Tỉ số giữa tiêu cự và độ dài trục thực của hypebol là tâm sai của hypebol và được kí hiệu là \(e\), tức là \(e = \dfrac{c}{a}\).
Nhận xét:
+ \(e = \dfrac{c}{a} > 1\)
+ \(e = \dfrac{{\sqrt {{a^2} + {b^2}} }}{a} = \sqrt {1 + {{\left( {\dfrac{b}{a}} \right)}^2}} \)
Ví dụ:
Tìm tâm sai của hypebol \(\left( H \right):\dfrac{{{x^2}}}{{64}} - \dfrac{{{y^2}}}{{36}} = 1\).
Giải
Ta có \(a = 8,b = 6\) suy ra \(c = \sqrt {{a^2} + {b^2}} = 10\)
Vậy tâm sai của (H) là \(e = \dfrac{c}{a} = \dfrac{{10}}{8} = \dfrac{5}{4}\).
IV. Bán kính qua tiêu của một điểm thuộc hypebol
Cho hypebol có phương trình chính tắc \(\dfrac{{{x^2}}}{{{a^2}}} - \dfrac{{{y^2}}}{{{b^2}}} = 1\) với các tiêu điểm \({F_1}\left( { - c;0} \right),\,{F_2}\left( {c;0} \right)\) (với \(c = \sqrt {{a^2} + {b^2}} \)). Với \(M\left( {x;y} \right)\) thuộc hypebol, ta có
\(M{F_1} = \left| {a + \dfrac{c}{a}x} \right|,M{F_2} = \left| {a - \dfrac{c}{a}x} \right|\)
Các đoạn thẳng \(M{F_1},\,M{F_2}\) được gọi là bán kính qua tiêu của điểm M.
Ví dụ:
Cho hypebol \(\dfrac{{{x^2}}}{4} - \dfrac{{{y^2}}}{{21}} = 1\). Tính độ dài bán kính qua tiêu của một điểm M thuộc hypebol và có hoành độ bằng -10.
Giải
Ta có: \({a^2} = 4;\,{b^2} = 21 \Rightarrow a = 4,\,b = \sqrt {21} \) và \(c = \sqrt {{a^2} + {b^2}} = 5\).
Do đó, hypebol có 2 tiêu điểm là \({F_1}\left( { - 5;0} \right),\,{F_2}\left( {5;0} \right)\).
Điểm M thuộc hypebol và có hoành độ \({x_0} = - 10\) nên:
\(M{F_1} = \left| {a + \dfrac{c}{a}{x_0}} \right| = \left| {2 + \dfrac{5}{2}.\left( { - 10} \right)} \right| = 23\)
\(M{F_2} = \left| {a - \dfrac{c}{a}{x_0}} \right| = \left| {2 - \dfrac{5}{2}.\left( { - 10} \right)} \right| = 27\)
V. Đường chuẩn của hypebol
Cho hypebol (H) có phương trình chính tắc \(\dfrac{{{x^2}}}{{{a^2}}} - \dfrac{{{y^2}}}{{{b^2}}} = 1\) và có hai tiêu điểm \({F_1}\left( {-c;0} \right),{F_2}\left( {c;0} \right).\)
Đường thẳng \({\Delta _1}:x + \dfrac{a}{e} = 0\) được gọi là đường chuẩn ứng với tiêu điểm \({F_1}\) và đường thẳng \({\Delta _2}:x - \dfrac{a}{e} = 0\) được gọi là đường chuẩn ứng với tiêu điểm \({F_2}\) của hypebol (H).
Với mọi điểm M thuộc hypebol, ta luôn có \(\dfrac{{M{F_1}}}{{d\left( {M;{\Delta _1}} \right)}} = \dfrac{{M{F_2}}}{{d\left( {M;{\Delta _2}} \right)}} = e\).
Chú ý: Vì \( - a < - \dfrac{a}{e} < \dfrac{a}{e} < a\) nên đường chuẩn của hypebol không có điểm chung với hypebol đó.
Ví dụ:
Cho điểm \(M\left( {x;y} \right)\) trên hypebol (H):\(\dfrac{{{x^2}}}{{{a^2}}} - \dfrac{{{y^2}}}{{{b^2}}} = 1\)
a) Tìm toạ độ hai tiêu điểm và viết phương trình hai đường chuẩn tương ứng.
b) Tính tỉ số khoảng cách từ M đến tiêu điểm và đến đường chuẩn tương ứng.
Giải
Ta có \(a = 4;{\rm{ }}b = 3,\) suy ra \(c = \sqrt {a + b} {\rm{ }} = 5,{\rm{ }}e = \dfrac{c}{a} = \dfrac{5}{4};\,\,\dfrac{a}{e} = \dfrac{{{a^2}}}{c} = \dfrac{{16}}{5}\)
a) Ứng với tiêu \({F_1}\left( {-5;0} \right)\), ta có đường chuẩn \({\Delta _1}:\,x + \dfrac{{16}}{5} = 0\)
Ứng với tiêu điểm \({F_{_2}}\left( {5;0} \right)\)ta có đường chuẩn \({\Delta _2}:\,x - \dfrac{{16}}{5} = 0\)
b) Ta có \(\dfrac{{M{F_1}}}{{d\left( {M;{\Delta _1}} \right)}} = \dfrac{{M{F_2}}}{{d\left( {M;{\Delta _2}} \right)}} = e = \dfrac{5}{4}\)
VI. Cách vẽ hypebol
Để vẽ hypebol \(\left( H \right):\,\dfrac{{{x^2}}}{{{a^2}}} - \dfrac{{{y^2}}}{{{b^2}}} = 1\left( {a > 0,{\rm{ }}b > 0} \right),\) ta có thể làm như sau:
- Vẽ bốn đường thẳng \(y = b,y = - b,x = a,x = - a\) và xác định hình chữ nhật cơ sở PQRS của hypebol.
- Vẽ hai đường tiệm cận PR, QS của hypebol.
- Vẽ từng nhánh của hypebol ở phía ngoài hình chữ nhật cơ sở, sao cho tiếp xúc với cạnh của hình chữ nhật cơ sở tại đỉnh của hypebol và đi qua những điểm cụ thể đã chọn, đồng thời nhận PR, QS làm hai đường tiệm cận.
