I. Xác định đường conic theo tâm sai, tiêu điểm và đường chuẩn
Trong mặt phẳng cho điểm F cố định và một đường thẳng A cố định không đi qua F.
Tập hợp các điểm M sao cho tỉ số \(\dfrac{{MF}}{{d\left( {M,\Delta } \right)}}\) bằng một số dương \(e\) cho trước được gọi là đường conic.
Điểm F gọi là tiêu điểm, đường thẳng \(\Delta \) gọi là đường chuẩn tương ứng với F và \(e\) gọi là tâm sai của đường conic.
Ta có:
- Nếu tâm sai \(e < 1\) thì đường conic nhận được là đường elip.
- Nếu tâm sai \(e = 1\) thì đường conic nhận được là đường parabol.
- Nếu tâm sai \(e > 1\) thì đường conic nhận được là đường hypebol.
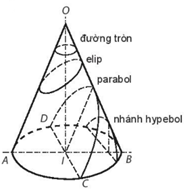
II. Giao của mặt phẳng với mặt nón tròn xoay
Giao của một mặt nón tròn xoay với một mặt phẳng không đi qua đỉnh là một đường tròn hoặc đường conic.
III. Một số ứng dụng của ba đường conic trong thực tiễn
Ba đường conic có một số tính chất trong thực tiễn sau:
- Một số ứng dụng trong quang học và âm học có thể kể đến là: chế đạo gương có dạng ba đường conic, chế tạo kính thiên văn,..
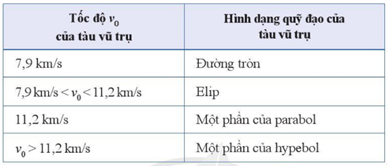
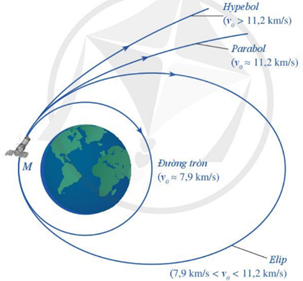
- Mô tả quỹ đạo của tàu vũ trụ:
Khi thiết lập quỹ đạo bay cho các con tàu vũ trụ phóng đi từ Trái Đất, các nhà khoa học luôn chọn quỹ đạo là đường conic. Hình dạng của quỹ đạo phụ thuộc vào tốc độ của tàu vũ trụ. Ta có bảng tương ứng giữa tốc độ và quỹ đạo như sau:
