Phương pháp giải các bài toán về hàm số bậc hai

I. Tìm điều kiện tham số để đồ thị hàm số đi qua điểm cho trước

Ví dụ: Tìm $m$ để đồ thị hàm số $y = {x^2} - mx + 1$ đi qua điểm $M\left( {1;2} \right)$.

Giải:

Đồ thị hàm số đi qua $M\left( {1;2} \right)$

$\Rightarrow$ thay $x = 1;y = 2$ ta được:

$2 = {1^2} - m.1 + 1 \Leftrightarrow 2 = 2 - m \Leftrightarrow m = 0$

Vậy $m = 0$ là giá trị cần tìm.

II. Viết phương trình parabol đi qua ba điểm

Ví dụ: Lập phương trình parabol đi qua các điểm $A\left( {0;0} \right),B\left( {1;1} \right),C\left( { - 1;1} \right)$.

Giải:

Gọi phương trình parabol $\left( P \right):y = a{x^2} + bx + c\left( {a \ne 0} \right)$.

Do $\left( P \right)$ đi qua các điểm $A\left( {0;0} \right),B\left( {1;1} \right),C\left( { - 1;1} \right)$ nên:

$\left\{ \begin{array}{l}0 = a{.0^2} + b.0 + c\\1 = a{.1^2} + b.1 + c\\1 = a.{\left( { - 1} \right)^2} + b.\left( { - 1} \right) + c\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}c = 0\\a + b = 1\\a - b = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b = 0\\c = 0\end{array} \right.$

Vậy phương trình parabol là $y = {x^2}$.

III. Viết phương trình parabol biết đỉnh và đi qua một điểm

Ví dụ: Lập phương trình parabol có đỉnh $\left( { - 1;3} \right)$ và đi qua điểm $\left( {0;4} \right)$.

Giải:

Gọi phương trình parabol $\left( P \right):y = a{x^2} + bx + c\left( {a \ne 0} \right)$

Do $\left( P \right)$ đi qua điểm $\left( {0;4} \right)$ và đỉnh $\left( { - 1;3} \right)$ nên:

$\left\{ \begin{array}{l}4 = a{.0^2} + b.0 + c\\ - \dfrac{b}{{2a}} =  - 1\\a.{\left( { - 1} \right)^2} + b.\left( { - 1} \right) + c = 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}c = 4\\b = 2a\\a - b + c = 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}c = 4\\a = 1\\b = 2\end{array} \right.$

Vậy phương trình parabol là $y = {x^2} + 2x + 4$.

IV. Biện luận số nghiệm của phương trình bậc hai theo tham số

(Áp dụng cho bài toán cô lập được $m$ từ phương trình).

Ví dụ: Biện luận số nghiệm của phương trình ${x^2} - x + m - 1 = 0$.

Giải:

Ta có: ${x^2} - x + m - 1 = 0 \Leftrightarrow m =  - {x^2} + x + 1$

Số nghiệm của phương trình đã cho chính là số giao điểm của đồ thị hàm số $y =  - {x^2} + x + 1$ với đường thẳng $y = m$.

Xét hàm số $y =  - {x^2} + x + 1$ có đồ thị là parabol như hình vẽ:

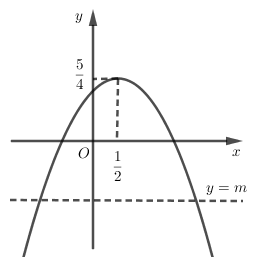
Quan sát đồ thị hàm số ta thấy:

+ Khi $m < \dfrac{5}{4}$ thì đường thẳng $y = m$ cắt đồ thị hàm số tại đúng $2$ điểm phân biệt.

Do đó phương trình đã cho có $2$ nghiệm phân biệt.

+ Khi $m = \dfrac{5}{4}$ thì đường thẳng $y = m$ tiếp xúc với đồ thị hàm số hay chỉ có $1$ điểm chung với đồ thị hàm số.

Do đó phương trình đã cho có $1$ nghiệm duy nhất.

+ Khi $m > \dfrac{5}{4}$ thì đường thẳng không cắt đồ thị hàm số hay không có điểm chung với đồ thị hàm số.

Do đó phương trình đã cho vô nghiệm.

Kết luận:

+ Nếu $m < \dfrac{5}{4}$ thì phương trình đã cho có $2$ nghiệm phân biệt.

+ Nếu $m = \dfrac{5}{4}$ thì phương trình đã cho có $1$ nghiệm duy nhất.

+ Nếu $m > \dfrac{5}{4}$ thì phương trình đã cho vô nghiệm.