I. Sơ đồ Hình cầu. Diện tích mặt cầu và thể tích hình cầu
II. Hình cầu. Diện tích mặt cầu và thể tích hình cầu
1. Các kiến thức cần nhớ
Hình cầu
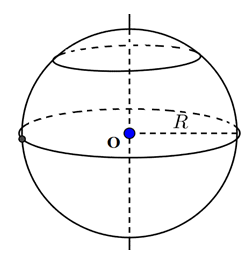
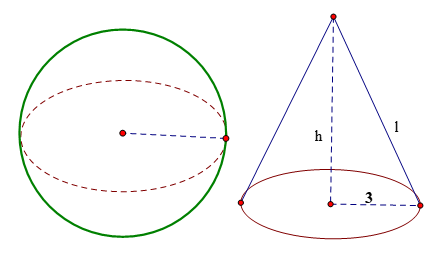
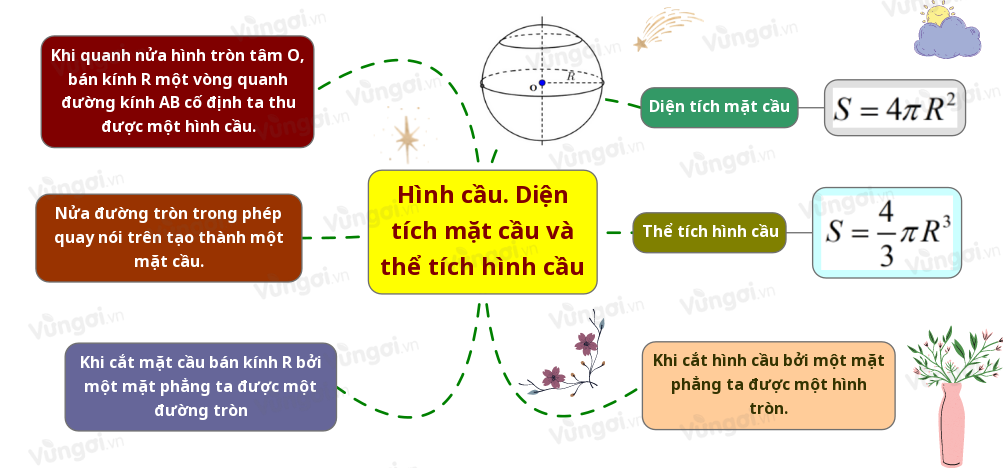
- Khi quanh nửa hình tròn tâm $O$, bán kính $R$ một vòng quanh đường kính $AB$ cố định ta thu được một hình cầu.
- Nửa đường tròn trong phép quay nói trên tạo thành một mặt cầu.
- Điểm $O$ gọi là tâm, $R$ là bán kính của hình cầu hay mặt cầu đó.
Chú ý:
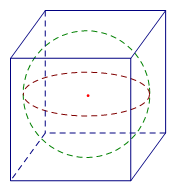
- Khi cắt hình cầu bởi một mặt phẳng ta được một hình tròn.
- Khi cắt mặt cầu bán kính $R$ bởi một mặt phẳng ta được một đường tròn, trong đó :
+ Đường tròn đó có bán kính $R$ nếu mặt phẳng đi qua tâm (gọi là đường kính lớn).
+ Đường tròn đó có bán kính bé hơn \(R\) nếu mặt phẳng không đi qua tâm.
Diện tích và thể tích
Cho hình cầu bán kính $R.$
- Diện tích mặt cầu: $S = 4\pi {R^2}$ .
- Thể tích hình cầu: \(V = \dfrac{4}{3}\pi {R^3}\).
2. Các dạng toán thường gặp
Dạng 1: Tính diện tích mặt cầu, thể tích hình cầu và bán kính hình cầu.
Phương pháp:
Ta sử dụng các công thức tính diện tích mặt cầu $S = 4\pi {R^2}$ và thể tích hình cầu : \(V = \dfrac{4}{3}\pi {R^3}\).
Dạng 2: Bài toán tổng hợp
Phương pháp:
Vận dụng các công thức trên và các kiến thức đã học để tính các đại lượng chưa biết rồi từ đó tính diện tích mặt cầu, thể tích hình cầu.
