I. Sơ đồ tư duy Sự tương giao giữa đường thẳng và Parabol

II. Sự tương giao giữa đường thẳng và parabol
1. Các kiến thức cần nhớ
Sự tương giao giữa đường thẳng $d:y = mx + n$ và parabol $\left( P \right):y = a{x^2}$$\left( {a \ne 0} \right).$
Hình minh họa
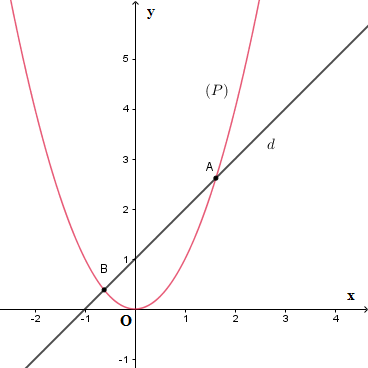
Số giao điểm của đường thẳng $d$ và parabol $\left( P \right)$ là số nghiệm của phương trình hoành độ giao điểm
$a{x^2} = mx + n \Leftrightarrow a{x^2} - mx - n = 0$(*)
+) Phương trình (*) có hai nghiệm phân biệt $\left( {\Delta > 0} \right)$thì $d$ cắt $\left( P \right)$ tại hai điểm phân biệt
+) Phương trình (*) có nghiệm kép $\left( {\Delta = 0} \right)$thì $d$ tiếp xúc với $\left( P \right)$.
+) Phương trình (*) vô nghiệm $\left( {\Delta < 0} \right)$thì $d$ không cắt $\left( P \right)$
2. Các dạng toán thường gặp
Dạng 1: Xác định số giao điểm của đường thẳng $d:y = mx + n$ và parabol $\left( P \right):y = a{x^2}$$\left( {a \ne 0} \right).$
Phương pháp:
Số giao điểm của đường thẳng $d$ và parabol $\left( P \right)$ là số nghiệm của phương trình hoành độ giao điểm
$a{x^2} = mx + n \Leftrightarrow a{x^2} - mx - n = 0$(*)
+) Phương trình (*) có hai nghiệm phân biệt $\left( {\Delta > 0} \right)$thì $d$ cắt $\left( P \right)$ tại hai điểm phân biệt
+) Phương trình (*) có nghiệm kép $\left( {\Delta = 0} \right)$thì $d$ tiếp xúc với $\left( P \right)$.
+) Phương trình (*) vô nghiệm $\left( {\Delta < 0} \right)$thì $d$ không cắt $\left( P \right)$
Dạng 2: Tìm tọa độ giao điểm của đường thẳng $d:y = mx + n$ và parabol $\left( P \right):y = a{x^2}$$\left( {a \ne 0} \right).$
Phương pháp:
Xét phương trình hoành độ giao điểm $a{x^2} = mx + n \Leftrightarrow a{x^2} - mx - n = 0$(*)
Giải phương trình (*) tìm được $x$ suy ra $y$ . Tọa độ giao điểm là $\left( {x;y} \right)$.
Dạng 3: Xác định tham số $m$ để đường thẳng $d:y = mx + n$ và parabol $\left( P \right):y = a{x^2}$$\left( {a \ne 0} \right)$ cắt nhau tại điểm thỏa mãn điều kiện cho trước .
Phương pháp:
+) Đường thẳng $d$ cắt $\left( P \right)$ tại hai điểm phân biệt nằm bên trái trục tung $ \Leftrightarrow $ phương trình (*) có hai nghiệm âm phân biệt $ \Leftrightarrow \left\{ \begin{array}{l}\Delta > 0\\S < 0\\P > 0\end{array} \right.$
+) Đường thẳng $d$ cắt $\left( P \right)$ tại hai điểm phân biệt cùng nằm bên phải trục tung $ \Leftrightarrow $ phương trình (*) có hai nghiệm dương phân biệt $ \Leftrightarrow \left\{ \begin{array}{l}\Delta > 0\\S > 0\\P > 0\end{array} \right.$
+) Đường thẳng $d$ cắt $\left( P \right)$ tại hai điểm phân biệt nằm khác phía trục tung $ \Leftrightarrow $ phương trình (*) có hai nghiệm trái dấu $ \Leftrightarrow ac < 0$
+) Đường thẳng $d$ cắt $\left( P \right)$ tại hai điểm có tọa độ thỏa mãn biểu thức cho trước (thường biến đổi biểu thức để sử dụng hệ thức Vi-et)
Dạng 4: Bài toán liên quan đến diện tích tam giác, diện tích hình thang và chiều cao.
Phương pháp:
Ta vận dụng linh hoạt các cách phân chia diện tích và công thức tính diện tích tam giác, hình thang để làm bài.

