I. Sơ đồ tư duy Hệ số góc của đường thẳng
II. Hệ số góc của đường thẳng
1. Các kiến thức cần nhớ
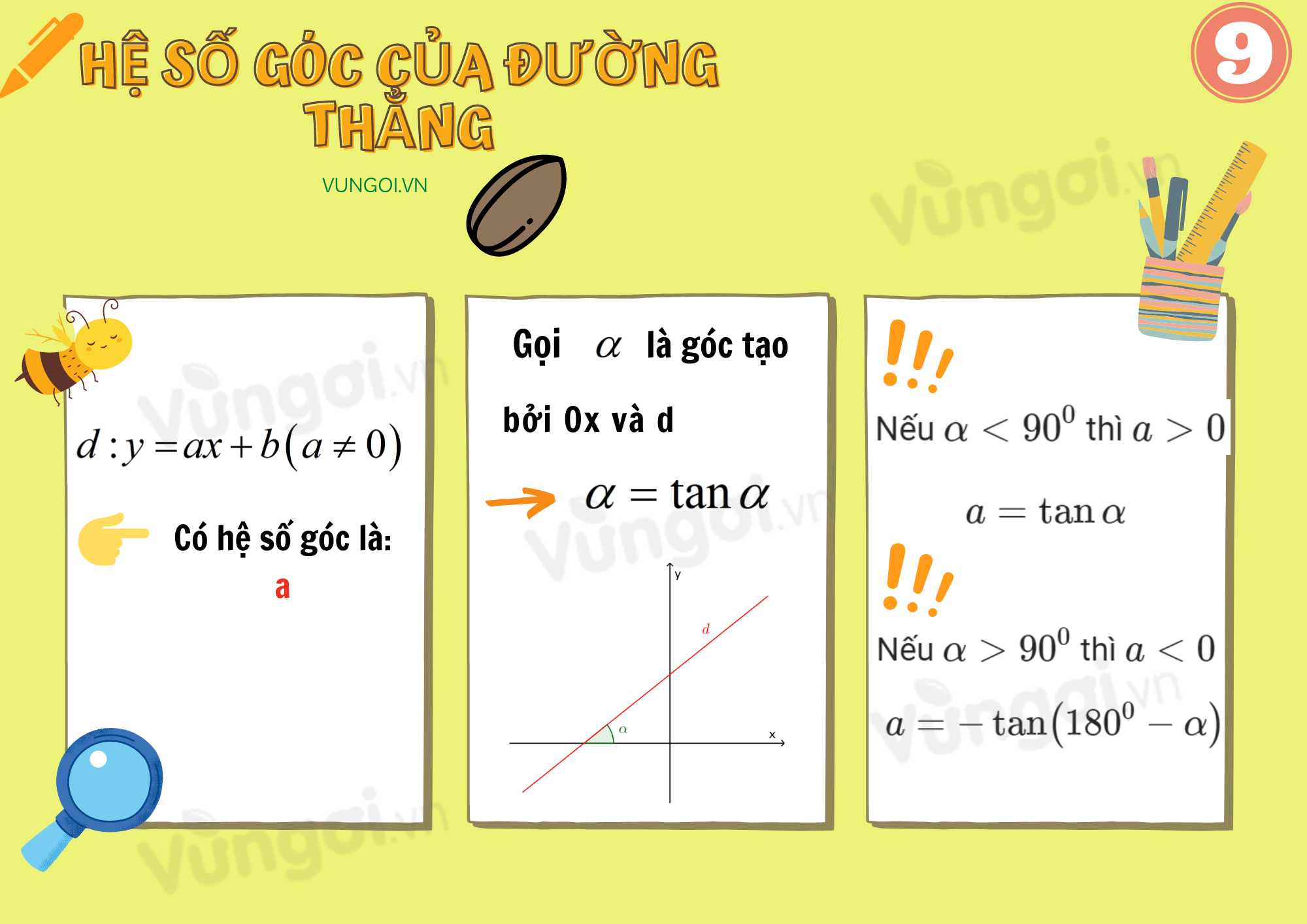
Hệ số góc của đường thẳng
Cho đường thẳng \(d\) có phương trình \(y = ax + b\,\left( {a \ne 0} \right)\).
Khi đó:
Số thực \(a\) là hệ số góc của \(d\) .
Gọi \(\alpha \) là góc tạo bởi tia \(Ox\) và \(d.\)
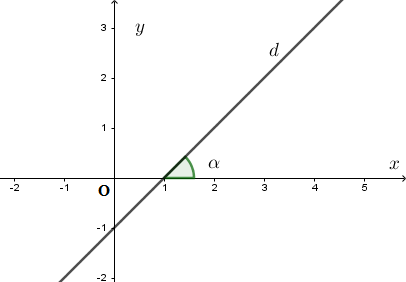
Ta có:
+ Nếu \(\alpha < {90^0}\) thì \(a > 0\) và $a = \tan \alpha $
+ Nếu \(\alpha > {90^0}\) thì \(a < 0\) và \(a = - \tan \left( {{{180}^0} - \alpha } \right)\).
Tính chất
Các đường thẳng có cùng hệ số góc thì tạo với trục $Ox$ các góc bằng nhau.
2. Các dạng toán thường gặp
Dạng 1: Xác định hệ số góc của đường thẳng
Phương pháp:
Đường thẳng $d$ có phương trình \(y = ax + b\,\left( {a \ne 0} \right)\)có $a$ là hệ số góc.
Dạng 2: Tính góc tạo bởi tia $Ox$ và đường thẳng $d$.
Phương pháp:
Gọi \(\alpha \) là góc tạo bởi tia \(Ox\) và \(d.\) Ta có: $a = \tan \alpha $
Dạng 3: Viết phương trình đường thẳng hoặc tìm tham số m khi biết hệ số góc
Phương pháp:
Gọi phương trình đường thẳng cần tìm là $y = ax + b\,\,\left( {a \ne 0} \right)$.
Dựa vào lý thuyết về hệ số góc để tìm $a$. Từ đó, sử dụng dữ kiện còn lại của đề bài để tìm $b$.
