1. Các kiến thức cần nhớ
Hệ thức giữa cạnh và góc trong tam giác vuông
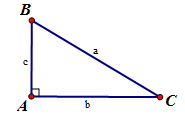
+) Cho tam giác $ABC$ vuông tại $A$ có $BC = a,AC = b,AB = c.$ Ta có:
$b = a.\sin B = a.\cos C$; $c = a.\sin C = a.\cos B;$
$b = c.\tan B = c.\cot C$; $c = b.\tan C = b.\cot B.$
+) Trong một tam giác vuông
Cạnh góc vuông = (Cạnh huyền) $ \times $ ( sin góc đối)
= (Cạnh huyền) $ \times $ ( côsin góc kề)
Cạnh góc vuông = (Cạnh góc vuông) $ \times $ (tang góc đối)
= (Cạnh góc vuông) $ \times $ (cotang góc kề)
2. Các dạng toán thường gặp
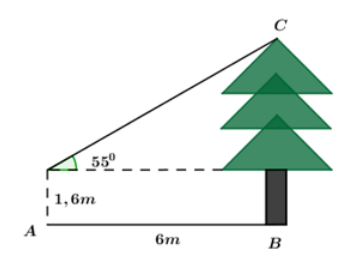
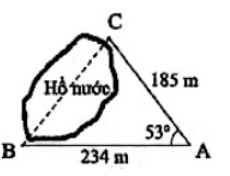
Dạng 1: Toán ứng dụng thực tế
Phương pháp:
Sử dụng hệ thức giữa cạnh và góc trong tam giác vuông để giải quyết bài toán thực tế.
+) Cho tam giác $ABC$ vuông tại $A$ có $BC = a,AC = b,AB = c.$ Ta có :
$b = a.\sin B = a.\cos C$; $c = a.\sin C = a.\cos B$;
$b = c.\tan B = c.\cot C$; $c = b.\tan C = b.\cot B$.
+) Trong một tam giác vuông
Cạnh góc vuông = (Cạnh huyền) $ \times $ ( sin góc đối)
= (Cạnh huyền) $ \times $ ( côsin góc kề)
Cạnh góc vuông = (Cạnh góc vuông) $ \times $ (tang góc đối)
= (Cạnh góc vuông) $ \times $ (cotang góc kề)
Dạng 2: Bài toán tổng hợp
Phương pháp:
Vận dụng linh hoạt các hệ thức lượng, các hệ thức giữa cạnh và góc trong tam giác vuông để tính toán.
