I. Sơ đồ tư duy Biến đổi đơn giản biểu thức chứa căn
II. Biến đổi đơn giản biểu thức chứa căn
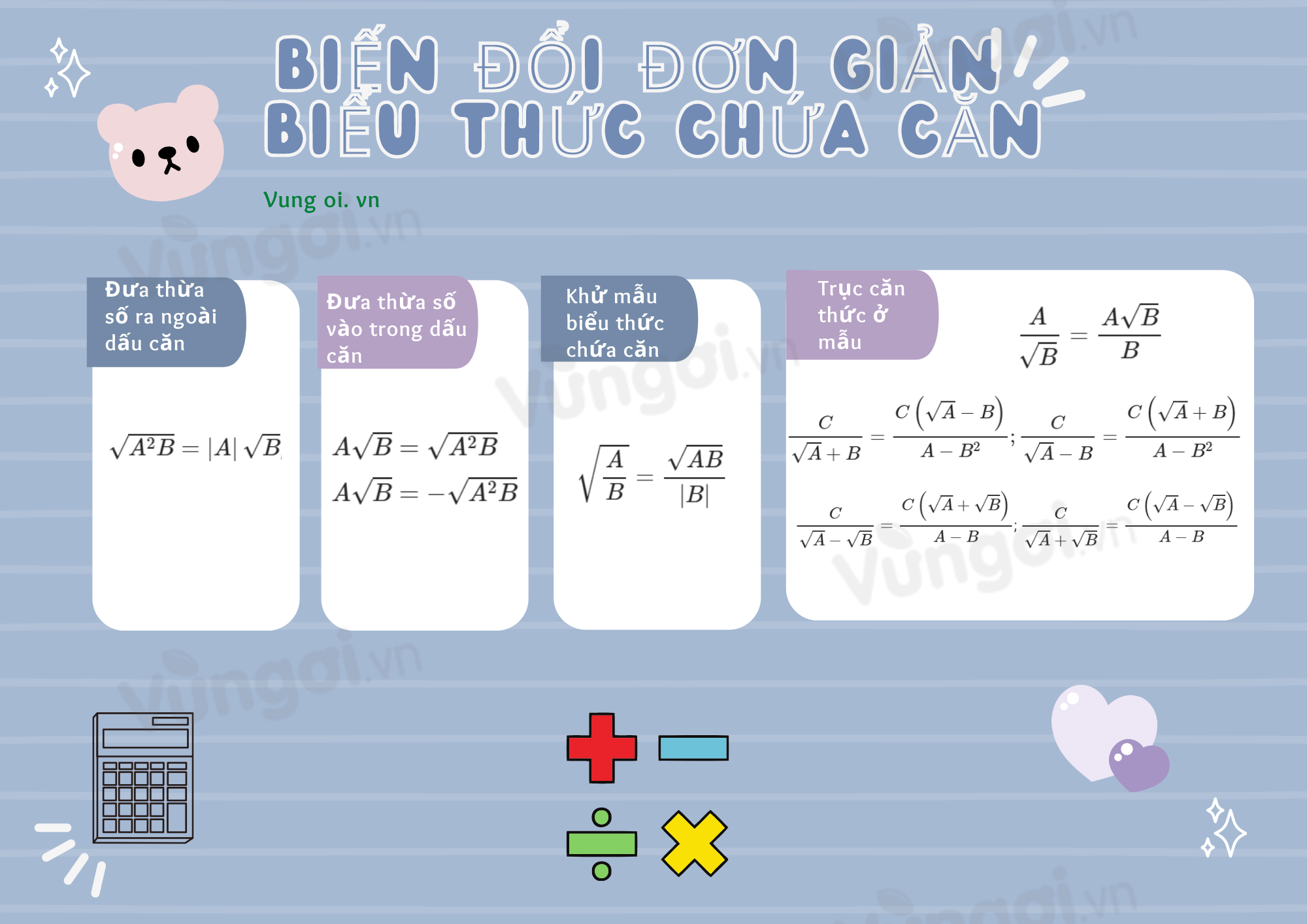
1. Các kiến thức cần nhớ
Đưa thừa số ra ngoài dấu căn
Với hai biểu thức $A,B$ mà $B \ge 0$, ta có $\sqrt {{A^2}B} = \left| A \right|\sqrt B $, tức là
+) Nếu $A \ge 0$ và $B \ge 0$ thì $\sqrt {{A^2}B} = A\sqrt B $
+) Nếu $A < 0$ và $B \ge 0$ thì $\sqrt {{A^2}B} = - A\sqrt B $
Đưa thừa số vào trong dấu căn
+) Với $A \ge 0$ và $B \ge 0$ ta có $A\sqrt B = \sqrt {{A^2}B} $
+) Với $A < 0$ và $B \ge 0$ ta có $A\sqrt B = - \sqrt {{A^2}B} $
Khử mẫu của biểu thức lấy căn
Với các biểu thức $A,B$ mà $A.B \ge 0;B \ne 0$, ta có $\sqrt {\dfrac{A}{B}} = \dfrac{{\sqrt {AB} }}{{\left| B \right|}}$
Trục căn thức ở mẫu
+) Với các biểu thức $A,B$ mà $B > 0$, ta có $\dfrac{A}{{\sqrt B }} = \dfrac{{A\sqrt B }}{B}$
+) Với các biểu thức $A,B,C$ mà $A \ge 0,A \ne {B^2}$, ta có $\dfrac{C}{{\sqrt A + B}} = \dfrac{{C\left( {\sqrt A - B} \right)}}{{A - {B^2}}};\dfrac{C}{{\sqrt A - B}} = \dfrac{{C\left( {\sqrt A + B} \right)}}{{A - {B^2}}}$
+) Với các biểu thức $A,B,C$ mà $A \ge 0,B \ge 0,A \ne B$ ta có
$\dfrac{C}{{\sqrt A - \sqrt B }} = \dfrac{{C\left( {\sqrt A + \sqrt B } \right)}}{{A - B}}$; $\dfrac{C}{{\sqrt A + \sqrt B }} = \dfrac{{C\left( {\sqrt A - \sqrt B } \right)}}{{A - B}}$
2. Một số dạng toán thường gặp
Dạng 1: Đưa thừa số vào trong dấu căn, đưa thừa số ra ngoài dấu căn
Phương pháp:
Sử dụng các công thức
* Đưa thừa số ra ngoài dấu căn
Với hai biểu thức $A,B$ mà $B \ge 0$, ta có $\sqrt {{A^2}B} = \left| A \right|\sqrt B = \left\{ \begin{array}{l}A\sqrt B \,\,{\rm{khi}}\,\,A \ge 0\\ - A\sqrt B \,{\rm{khi}}\,A < 0\end{array} \right.$
* Đưa thừa số vào trong dấu căn
+) $A\sqrt B = \sqrt {{A^2}B} $ với $A \ge 0$ và $B \ge 0$
+) $A\sqrt B = - \sqrt {{A^2}B} $ với $A < 0$ và $B \ge 0$
Dạng 2: So sánh hai căn bậc hai
Phương pháp:
Sử dụng công thức đưa thừa số ra ngoài dấu căn hoặc đưa thừa số vào trong dấu căn để so sánh hai căn bậc hai theo mối liên hệ
$0 \le A < B \Leftrightarrow \sqrt A < \sqrt B $
Dạng 3: Rút gọn biểu thức chứa căn thức bậc hai
Phương pháp:
Sử dụng công thức đưa thừa số ra ngoài dấu căn hoặc đưa thừa số vào trong dấu căn và hằng đẳng thức $\sqrt {{A^2}} = \left| A \right|$.
Sử dụng công thức trục căn thức ở mẫu
Dạng 4: Trục căn thức ở mẫu
Phương pháp:
Sử dụng các công thức
+) Với các biểu thức $A,B$ mà $A.B \ge 0;B \ne 0$, ta có $\sqrt {\dfrac{A}{B}} = \dfrac{{\sqrt {AB} }}{{\left| B \right|}}$
+) Với các biểu thức $A,B$ mà $B > 0$, ta có $\dfrac{A}{{\sqrt B }} = \dfrac{{A\sqrt B }}{B}$
+) Với các biểu thức $A,B,C$ mà $A \ge 0,A \ne {B^2}$, ta có $\dfrac{C}{{\sqrt A + B}} = \dfrac{{C\left( {\sqrt A - B} \right)}}{{A - {B^2}}};\dfrac{C}{{\sqrt A - B}} = \dfrac{{C\left( {\sqrt A + B} \right)}}{{A - {B^2}}}$
+) Với các biểu thức $A,B,C$ mà $A \ge 0,B \ge 0,A \ne B$ ta có
$\dfrac{C}{{\sqrt A - \sqrt B }} = \dfrac{{C\left( {\sqrt A + \sqrt B } \right)}}{{A - B}}$; $\dfrac{C}{{\sqrt A + \sqrt B }} = \dfrac{{C\left( {\sqrt A - \sqrt B } \right)}}{{A - B}}$
Dạng 5: Giải phương trình
Phương pháp:
+) Tìm điều kiện
+) Sử dụng công thức đưa thừa số ra ngoài dấu căn hoặc đưa thừa số vào trong dấu căn để đưa phương trình về dạng cơ bản
+) So sánh điều kiện rồi kết luận nghiệm.
