I. Sơ đồ vị trí tương đối giữa đường thẳng và đường tròn
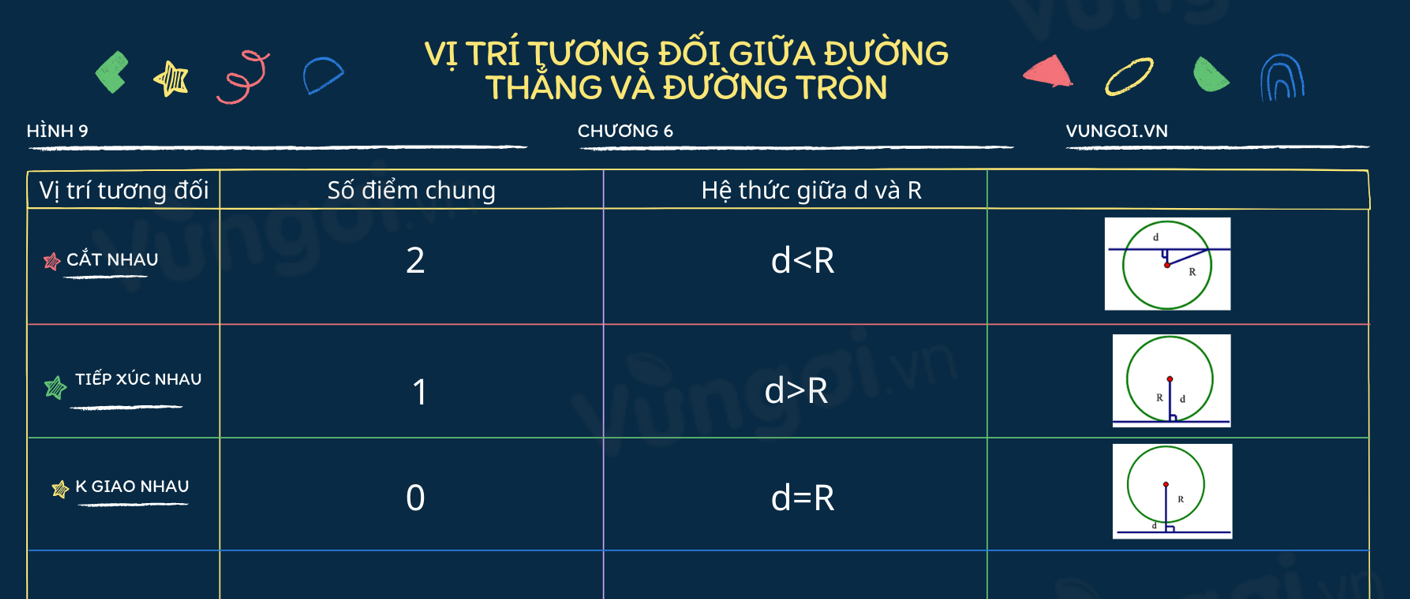
II. Vị trí tương đối giữa đường thẳng và đường tròn
1. Các kiến thức cần nhớ
Vị trí tương đối của đường thẳng và đường tròn
Cho đường tròn $\left( {O;R} \right)$ và một đường thẳng $\Delta $ bất kì. Gọi $d$ là khoảng cách từ tâm $O$ của đường tròn đến đường thẳng đó.
Trường hợp 1: Đường thẳng $\Delta $ và đường tròn $\left( {O;R} \right)$ cắt nhau.
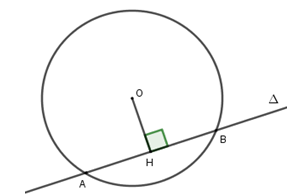
Khi đó, đường thẳng và đường tròn có hai điểm chung và khoảng cách $d = OH < R$
Trường hợp 2: Đường thẳng $\Delta $ và đường tròn $\left( {O;R} \right)$ tiếp xúc với nhau.
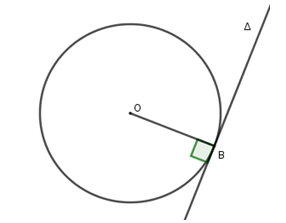
Khi đó, đường thẳng và đường tròn có một điểm chung và khoảng cách $d = OB = R$.
Đường thẳng $\Delta $ được gọi là tiếp tuyến của đường tròn và điểm $B$ là tiếp điểm.
Trường hợp 3: Đường thẳng $\Delta $ và đường tròn $\left( {O;R} \right)$ không giao nhau.
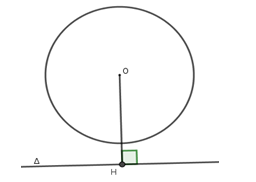
Khi đó, đường thẳng và đường tròn không có điểm chung và khoảng cách $d = OH > R$
Từ đó ta có bảng vị trí tương đối của đường thẳng và đường tròn.
|
Vị trí tương đối của đường thẳng và đường tròn |
Số điểm chung |
Hệ thức giữa $d$ và $R$ |
|
Đường thẳng và đường tròn cắt nhau |
$2$ |
$d < R$ |
|
Đường thẳng và đường tròn tiếp xúc nhau |
$1$ |
$d = R$ |
|
Đường thẳng và đường tròn không giao nhau |
$0$ |
$d > R$ |
Định lý:
Nếu một đường thẳng là tiếp tuyến của đường tròn thì nó vuông góc với bán kính đi qua tiếp điểm.
2. Các dạng toán thường gặp
Dạng 1: Xác định vị trí tương đối của đường thẳng và đường tròn
Phương pháp:
Dựa vào bảng vị trí tương đối :
|
Vị trí tương đối của đường thẳng và đường tròn |
Số điểm chung |
Hệ thức giữa $d$ và $R$ |
|
Đường thẳng và đường tròn cắt nhau |
$2$ |
$d < R$ |
|
Đường thẳng và đường tròn tiếp xúc nhau |
$1$ |
$d = R$ |
|
Đường thẳng và đường tròn không giao nhau |
$0$ |
$d > R$ |
Dạng 2: Bài toán độ dài dựa vào tính chất tiếp tuyến.
Phương pháp:
Sử dụng tính chất tiếp tuyến và định lý Pytago
Dạng 3: Tìm tập hợp điểm thỏa mãn điều kiện cho trước.
Phương pháp:
Sử dụng tính chất đường phân giác và các đường thẳng song song cách đều để tìm tập hợp điểm.
