Câu hỏi:
2 năm trước
Cho đường tròn $\left( {O;R} \right)$ và dây $AB = 1,2R$. Vẽ một tiếp tuyến song song với $AB$, cắt các tia $OA,OB$ lần lượt tại $E$ và $F$. Tính diện tích tam giác $OEF$ theo $R$.
Trả lời bởi giáo viên
Đáp án đúng: a
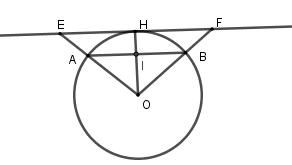
Kẻ $OH \bot EF$ tại $H$ và cắt $AB$ tại $I$ suy ra $OI \bot AB$ ( vì $AB{\rm{//}}EF$)
Xét $\left( O \right)$ có $OI \bot AB$ tại $I$ nên $I$ là trung điểm của $AB$ (liên hệ giữa đường kính và dây)
$ \Rightarrow IA = IB = \dfrac{{AB}}{2} = 0,6R$. Lại có $OA = R$.
Áp dụng định lý Pytago cho tam giác vuông $OIA$ ta có $OI = \sqrt {O{A^2} - I{A^2}} = 0,8R$.
Mà $AI\,{\rm{//}}\,EH$ nên $\dfrac{{AI}}{{EH}} = \dfrac{{OI}}{{OH}} = \dfrac{{0,8R}}{R} \Rightarrow EH = \dfrac{{0,6R}}{{0,8}} = 0,75R$
$\Delta OEF$cân tại $O$ (vì $\widehat E = \widehat F = \widehat {BAO} = \widehat {ABO}$) có $OH \bot EF$ nên $H$ là trung điểm của $EF$
$ \Rightarrow EF = 2EH = 1,5R$$ \Rightarrow {S_{EOF}} = \dfrac{{OH.EF}}{2} = 0,75{R^2}$.
Hướng dẫn giải:
Sử dụng định lý về tiếp tuyến của đường tròn, liên hệ giữa đường kính và dây, định lý Pytago để tính toán.
Câu hỏi khác
- Bài tập tính chất hai tiếp tuyến cắt nhau toán 9 có lời giải
- Bài tập sự xác định của đường tròn- tính chất đối xứng của đường tròn toán 9 có lời giải
- Bài tập vị trí tương đối giữa đường thẳng và đường tròn toán 9 có lời giải
- Bài tập đường kính và dây của đường tròn toán 9 có lời giải
- Bài tập dấu hiệu nhận biết tiếp tuyến của đường tròn toán 9 có lời giải
