Câu hỏi:
2 năm trước
Cho đường tròn \(\left( {O;6cm} \right)\) và dây \(AB = 9,6cm\). Vẽ một tiếp tuyến song song với \(AB\), cắt các tia \(OA,OB\) lần lượt tại \(E\) và \(F\). Tính diện tích tam giác \(OEF\) theo \(R\).
Trả lời bởi giáo viên
Đáp án đúng: c
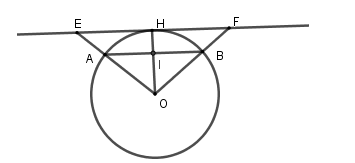
Kẻ \(OH \bot EF\) tại \(H\) và cắt \(AB\) tại \(I\) suy ra \(OI \bot AB\) ( vì \(AB{\rm{//}}EF\))
Xét \(\left( O \right)\) có \(OI \bot AB\) tại \(I\) nên \(I\) là trung điểm của \(AB\) (liên hệ giữa đường kính và dây)
\( \Rightarrow IA = IB = \dfrac{{AB}}{2} = 4,8\,cm\). Lại có \(OA = 6\,cm\).
Áp dụng định lý Pytago cho tam giác vuông \(OIA\) ta có \(OI = \sqrt {O{A^2} - I{A^2}} = \sqrt {{6^2} - 4,{8^2}} = 3,6\,cm\).
Mà \(AI\,{\rm{//}}\,EH\) nên \(\dfrac{{AI}}{{EH}} = \dfrac{{OI}}{{OH}} = \dfrac{{3,6}}{6} = \dfrac{3}{5}\)\( \Rightarrow EH = \dfrac{{AI.5}}{3} = \dfrac{{4,8.5}}{3} = 8\)
\(\Delta OEF\) cân tại \(O\) (vì \(\widehat E = \widehat F = \widehat {BAO} = \widehat {ABO}\)) có \(OH \bot EF\) nên \(H\) là trung điểm của \(EF\)
\( \Rightarrow EF = 2EH = 16\,cm\)\( \Rightarrow {S_{EOF}} = \dfrac{{6.16}}{2} = 48\,\left( {c{m^2}} \right)\).
Hướng dẫn giải:
Sử dụng định lý về tiếp tuyến của đường tròn, liên hệ giữa đường kính và dây, định lý Pytago để tính toán.
Diện tích tam giác bằng nửa tích của cạnh đáy và chiều cao tương ứng.
Câu hỏi khác
- Bài tập tính chất hai tiếp tuyến cắt nhau toán 9 có lời giải
- Bài tập sự xác định của đường tròn- tính chất đối xứng của đường tròn toán 9 có lời giải
- Bài tập vị trí tương đối giữa đường thẳng và đường tròn toán 9 có lời giải
- Bài tập đường kính và dây của đường tròn toán 9 có lời giải
- Bài tập dấu hiệu nhận biết tiếp tuyến của đường tròn toán 9 có lời giải
