Câu hỏi:
3 năm trước
Cho đường tròn (O; R) đường kính AB. Vẽ các tia tiếp tuyến Ax, By với nửa đường tròn. Lấy điểm M di động trên tía Ax, điểm N di động trên tia Oy sao cho \(AM.BN = {R^2}.\)
Chọn câu đúng.
Trả lời bởi giáo viên
Đáp án đúng: a
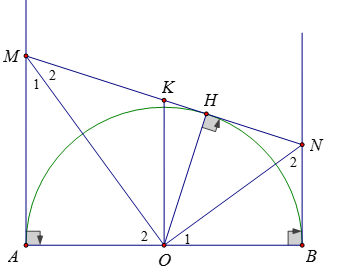
Gọi K là trung điểm của MN
Tam giác MON vuông tại O có OK là trung tuyến \( \Rightarrow KM = KN = KO\)
Suy ra: Đường tròn (K; KO) là đường tròn ngoại tiếp tam giác OMN.
Ta có OK là đường trung bình của hình thang AMNB nên \(OK // AM\)
\( \Rightarrow OK \bot AB\)
Suy ra OK là tiếp tuyến của đường tròn (K). Vậy đường tròn (K) ngoại tiếp tam giác OMN luôn tiếp xúc với một đường thẳng cố định là đường thẳng AB.
Hướng dẫn giải:
Gọi K là trung điểm của MN
Sử dụng tính chất tam giác vuông và tính chất đường trung bình của hình thang.


