Câu hỏi:
2 năm trước
Cho đường tròn tâm \(O\) bán kính \(6cm\) và một điểm \(A\) cách \(O\) là \(10cm\). Kẻ tiếp tuyến \(AB\) với đường tròn ( \(B\) là tiếp điểm). Tính độ dài \(AB\).
Trả lời bởi giáo viên
Đáp án đúng: d
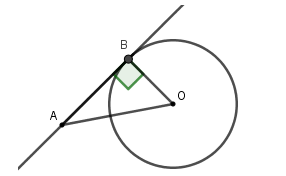
Vì \(AB\) là tiếp tuyến và \(B\) là tiếp điểm nên \(OB = R = 6\,cm\); \(AB \bot OB\) tại \(B\).
Áp dụng định lý Pytago cho tam giác \(ABO\) vuông tại \(B\) ta được \(AB = \sqrt {O{A^2} - O{B^2}} = \sqrt {{{10}^2} - {6^2}} = 8\,cm\)
Vậy \(AB = \,8\,cm\).
Hướng dẫn giải:
Sử dụng định lý về tiếp tuyến của đường tròn và định lý Pytago để tính toán