Kết quả:
0/20
Thời gian làm bài: 00:00:00
Cho đường tròn \(\left( O \right)\)có hai dây \(AB,CD\) không đi qua tâm. Biết rằng khoảng cách từ tâm \(O\) đến dây \(AB\) lớn hơn khoảng cách từ tâm \(O\) đến dây \(CD\). Kết luận nào sau đây là đúng?
Cho \(\left( {O;4cm} \right)\). Đường thẳng \(d\) là tiếp tuyến của đường tròn \(\left( {O;4\,cm} \right)\), khi đó
Cho đường tròn $\left( O \right)$ có bán kính $R = 5\,cm$. Khoảng cách từ tâm đến dây $AB$ là $3\,cm$. Tính độ dài dây $AB$.
Cho đường tròn \(\left( O \right)\) và điểm \(A\) nằm trên đường tròn \(\left( O \right).\) Nếu đường thẳng \(d \bot OA\) tại \(A\) thì
Đường tròn là hình:
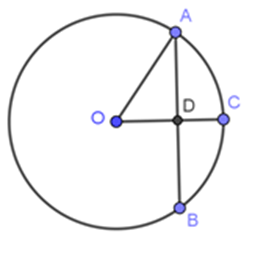
Trong hình vẽ bên cho $OC \bot AB,AB = 12cm,OA = 10cm$. Độ dài $AC$ là:
Cho đường tròn $\left( {O;3cm} \right)$, lấy điểm $A$ sao cho $OA = 6cm$. Từ \(A\) vẽ tiếp tuyến $AB,AC$ đến đường tròn $\left( O \right)$ ($B,C$ là tiếp điểm). Chu vi tam giác $ABC$ là
Tứ giác $AMON$ là hình gì?
Điểm $A$ phải cách $O$ một khoảng là bao nhiêu để cho $MN$ là tiếp tuyến của $\left( O \right)$?
Chọn câu sai.
Hình thang $ABDC$ có chu vi nhỏ nhất là
Cho tam giác $ABC$ vuông tại $A$, đường cao $AH$. Đường tròn đường kính $BH$ cắt $AB$ tại $D$, đường tròn đường kính $CH$ cắt $AC$ tại $E$ . Chọn khẳng định sai trong các khẳng định sau
Cho đường tròn tâm \(O\) bán kính \(6cm\) và một điểm \(A\) cách \(O\) là \(10cm\). Kẻ tiếp tuyến \(AB\) với đường tròn ( \(B\) là tiếp điểm). Tính độ dài \(AB\).
Cho đường tròn \((O).\) Từ một điểm \(M\) ở ngoài \((O)\), vẽ hai tiếp tuyến \(MA\) và \(MB\) sao cho góc \(AMB\) bằng \({60^0}\). Biết chu vi tam giác \(MAB\) là \(24\,cm\), tính độ dài bán kính đường tròn.
Cho hai đường tròn $\left( O \right);\left( {O'} \right)$ cắt nhau tại $A,B$, trong đó $O' \in \left( O \right)$. Kẻ đường kính $O'OC$ của đường tròn $\left( O \right)$. Chọn khẳng định sai?
Cho hai đường tròn \(\left( O \right)\) và \(\left( {O'} \right)\)tiếp xúc ngoài tại \(A\). Kẻ các đường kính \(AOB;AO'C\). Gọi \(DE\) là tiếp tuyến chung của hai đường tròn \(\left( {D \in \left( O \right);E \in \left( {O'} \right)} \right)\). Gọi \(M\) là giao điểm của \(BD\) và \(CE\). Tính diện tích tứ giác \(ADME\) biết \(\widehat {DOA} = 60^\circ \) và \(OA = 8\,cm\)
Cho hai đường tròn $\left( {O;5} \right)$ và $\left( {O';5} \right)$ cắt nhau tại $A$ và $B.$ Biết $OO' = 8.$ Độ dài dây cung $AB$ là
Chọn câu đúng.
Cho \(FK = 4cm.\) Khi đó:
Cho \(\widehat {xOy}\) , trên Ox lấy P, trên Oy lấy Q sao cho chu vi ∆POQ bằng 2a không đổi. Chọn câu đúng.

