Trả lời bởi giáo viên
Đáp án đúng: a
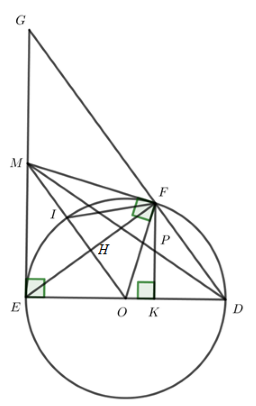
Gọi G là giao điểm của tia DF và tia EM.
Ta có \(\angle EFD = {90^o}\) (góc nội tiếp chắn nửa đường tròn) \( \Rightarrow EF \bot DG\) mà \(EF \bot OM\) (cmt)
\( \Rightarrow OM//DG\) (từ vuông góc đến song song)
Tam giác EDG có \(OE = OD\,\,;\,\,OM//DG\,\, \Rightarrow ME = MG\)(tính chất đường trung bình)
Áp dụng định lý Ta-let cho tam giác EDM có \(PK//ME\) (cùng vuông góc với ED) ta được: \(\dfrac{{PK}}{{ME}} = \dfrac{{DP}}{{DM}}\) (3)
Áp dụng định lý Ta-let cho tam giác MDG có \(PF//MG\) (cùng vuông góc với ED) ta được: \(\dfrac{{PF}}{{MG}} = \dfrac{{DP}}{{DM}}\) (4)
Từ (3) và (4) suy ra \(\dfrac{{PK}}{{ME}} = \dfrac{{PF}}{{MG}}\) mà \(ME = MG\) (cmt)
\( \Rightarrow PK = PF\,\, \Rightarrow \) P là trung điểm của FK. Suy ra \(FP = PK = \dfrac{4}{2} = 2cm\)
Hướng dẫn giải:
Kéo dài DF và EM cắt nhau tại G từ đó sử dụng định lý Ta-let để chứng minh.
Câu hỏi khác
- Đề kiểm tra 15 phút chương 6: đường tròn - đề số 2 Toán 9 có lời giải chi tiết
- Đề kiểm tra 15 phút chương 6: đường tròn - đề số 1 Toán 9 có lời giải chi tiết
- Đề kiểm tra 45 phút chương 6: đường tròn - đề số 2 Toán 9 có lời giải chi tiết
- Đề kiểm tra 45 phút chương 6: đường tròn - đề số 1 Toán 9 có lời giải chi tiết
