Tìm kiếm
Câu hỏi:
2 năm trước

Trong hình vẽ bên cho $OC \bot AB,AB = 12cm,OA = 10cm$. Độ dài $AC$ là:

Đề kiểm tra 45 phút chương 6: Đường tròn - Đề số 2 - ảnh 1

a.

$8cm$                    
b.

$2\sqrt {10} cm$
c.

$4\sqrt 7 cm$
d.

$2cm$
Xem đáp án
89 lượt xem
BẮT ĐẦU THI THỬ

Trả lời bởi giáo viên

Đáp án đúng: b

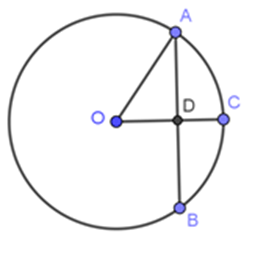
Vì $OC$ vuông góc với $AB$ nên $D$ là trung điểm của $AB$ (mối quan hệ giữa đường kính và dây)

$ \Rightarrow AD = \dfrac{{AB}}{2} = \dfrac{{12}}{2} = 6cm$.

Xét tam giác $AOD$ vuông tại $D$ nên $O{D^2} = O{A^2} - A{D^2} = {10^2} - {6^2} = 64 \Rightarrow OD = 8cm$.

Có $OD + DC = OC$ nên $DC = OC - OD = 10 - 8 = 2cm$.

Xét tam giác $ADC$ vuông tại $D$ nên $A{C^2} = A{D^2} + D{C^2} = {6^2} + {2^2} = 40$ .

Vậy $AC = 2\sqrt {10} cm$.

Hướng dẫn giải:

Dựa vào tính chất bán kính vuông góc với dây cung.

Dựa vào định lí Pi-ta-go trong tam giác vuông.

Câu hỏi khác

Câu 1:

Cho đường tròn \(\left( O \right)\)có hai dây \(AB,CD\) không đi qua tâm. Biết rằng khoảng cách từ tâm \(O\) đến dây \(AB\) lớn hơn khoảng cách từ tâm \(O\) đến dây \(CD\).  Kết luận nào sau đây là đúng?

\(AB > CD\)

\(AB = CD\)

\(AB < CD\)

\(AB{\rm{//}}CD\)
113
113 lượt xem
Xem đáp án
2 năm trước
Câu 2:

Cho \(\left( {O;4cm} \right)\). Đường thẳng \(d\) là tiếp tuyến của đường tròn \(\left( {O;4\,cm} \right)\), khi đó

Khoảng cách từ \(O\) đến đường thẳng \(d\) nhỏ hơn \(4\,cm\)        

Khoảng cách từ \(O\) đến đường thẳng \(d\) bằng \(4\,cm\)

Khoảng cách từ \(O\) đến đường thẳng \(d\) lớn hơn \(4\,cm\)         

Khoảng cách từ \(O\) đến đường thẳng \(d\) bằng \(5\,cm\)
77
77 lượt xem
Xem đáp án
2 năm trước
Câu 3:

Cho đường tròn $\left( O \right)$ có bán kính $R = 5\,cm$. Khoảng cách từ tâm đến dây $AB$ là $3\,cm$. Tính độ dài dây $AB$.

$AB = 6\,cm$

$AB = 8\,cm$

$AB = 10\,cm$

$AB = 12\,cm$
152
152 lượt xem
Xem đáp án
2 năm trước
Câu 4:

Cho đường tròn \(\left( O \right)\) và điểm \(A\) nằm trên đường tròn \(\left( O \right).\) Nếu đường thẳng  \(d \bot OA\) tại \(A\)  thì

\(d\) là tiếp tuyến của \(\left( O \right)\)

\(d\) cắt \(\left( O \right)\) tại hai điểm phân biệt

\(d\) là tiếp xúc với \(\left( O \right)\) tại \(O\)

Cả A, B, C đều sai
102
102 lượt xem
Xem đáp án
2 năm trước
Câu 5:

Đường tròn là hình:

Không có trục đối xứng                                       

Có một trục đối xứng

Có hai trục đối xứng                                      

Có vô số trục đối xứng
109
109 lượt xem
Xem đáp án
2 năm trước
Câu 7:

Cho đường tròn $\left( {O;3cm} \right)$, lấy điểm $A$ sao cho $OA = 6cm$. Từ \(A\) vẽ tiếp tuyến $AB,AC$ đến đường tròn $\left( O \right)$  ($B,C$ là tiếp điểm). Chu vi tam giác $ABC$ là

$9cm$                      

$9\sqrt 3 cm$                  

$9\sqrt 2 cm$                    

Kết quả khác
105
105 lượt xem
Xem đáp án
2 năm trước

Đề thi - đề kiểm tra Xem thêm
icon Hỏi bài tập
Hỏi bài tập Xem thêm
Học lý thuyết MÔN TOÁN Lớp 9 vững kiến thức đứng top 1 lớp