Kết quả:
0/15
Thời gian làm bài: 00:00:00
Cho hình cầu có đường kính \(d = 6\,cm\) . Diện tích mặt cầu là
Cho hình nón có chiều cao \(h = 10\,cm\) và thể tích \(V = 1000\pi \,\left( {c{m^3}} \right)\) . Tính diện tích toàn phần của hình nón
Cho hình thang vuông $ABDC$ vuông tại $A$ và $B$ , biết cạnh $AB = BC = 3m,AD = 5cm$. Tính diện tích xung quanh hình nón cụt tạo thành khi quay hình thang quanh cạnh $AB$ .
Hộp sữa ông Thọ có dạng hình trụ (đã bỏ nắp) có chiều cao \(h = 12cm\) và đường kính đáy là \(d= 8\,cm\) . Tính diện tích toàn phần của hộp sữa. Lấy \(\pi \simeq 3,14\)
Cho hình trụ có bán kính đáy \(R = 4\,\left( {cm} \right)\) và chiều cao \(h = 5\,\left( {cm} \right)\) . Diện tích xung quanh của hình trụ là
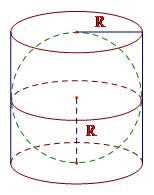
Cho một hình cầu nội tiếp trong hình trụ. Biết rằng đường kính đáy và chiều cao của hình trụ bằng nhau và bằng đường kính của hình cầu. Tính tỉ số giữa thể tích hình cầu và thể tích hình trụ.
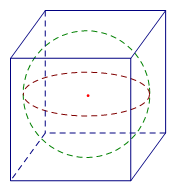
Cho một hình cầu và một hình lập phương ngoại tiếp nó. Tính tỉ số giữa diện tích mặt cậu và diện tích toàn phần của hình lập phương.
Tính diện tích xung quanh của một hình trụ có bán kính đáy là $4\,cm$ và chiều cao là \(6\,cm\) .
Nếu ta tăng bán kính đáy và chiều cao của một hình nón lên hai lần thì diện tích xung quanh của hình nón đó
Cho mặt cầu có thể tích \(V = 288\pi \,\left( {c{m^3}} \right)\) . Tính đường kính mặt cầu.
Một hình trụ có thể tích \(V\) không đổi. Hỏi bán kính đáy bằng bao nhiêu để diện tích toàn phần của hình trụ đó là nhỏ nhất.
Cho tam giác \(ABC\) đều cạnh \(a\) , đường trung tuyến \(AM\) . Quay tam giác \(ABC\) quanh cạnh \(AM\) . Tính diện tích toàn phần của hình nón tạo thành.
Cho hình chữ nhật \(ABCD\) có \(AB = 4\,cm;AD = 3\,cm\) . Tính diện tích mặt cầu thu được khi quay nửa đường tròn ngoại tiếp hình chữ nhật \(ABCD\) quay quanh đường thẳng \(MN\) với \(M\) là trung điểm \(AD\) , \(N\) là trung điểm \(BC\) .
Một hình nón có diện tích xung quanh bằng $960\;c{m^2}$ , chu vi đáy bằng $48\,\left( {cm} \right).$ Đường sinh của hình nón đó bằng
Cho một hình trụ, một hình nón và một hình cầu có thể tích bằng nhau. Bán kính đáy của hình trụ, bán kính đáy của hình nón và bán kính của hình cầu đều bằng $R.$ Tính các chiều cao \({h_1}\) của hình trụ và \({h_2}\) của hình nón theo \(R.\)

