Câu hỏi:
2 năm trước
Cho hình chữ nhật \(ABCD\) có \(AB = 4\,cm;AD = 3\,cm\) . Tính diện tích mặt cầu thu được khi quay nửa đường tròn ngoại tiếp hình chữ nhật \(ABCD\) quay quanh đường thẳng \(MN\) với \(M\) là trung điểm \(AD\) , \(N\) là trung điểm \(BC\) .
Trả lời bởi giáo viên
Đáp án đúng: a
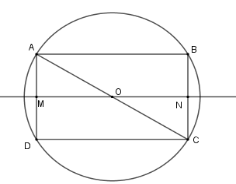
Gọi \(O\) là tâm của hình chữ nhật nên $OA = OB = OC = OD$ nên \(O\) là tâm đường tròn ngoại tiếp hình chữ nhật \(ABCD\) . Khi đó bán kính đường tròn là \(R = OA = \dfrac{{AC}}{2}\)
Theo định lý Pytago ta có \(A{C^2} = A{D^2} + D{C^2} = {3^2} + {4^2} = 25 \Rightarrow AC = 5\) (vì \(AB = DC = 4\,cm\) )\( \Rightarrow R = \dfrac{5}{2}\)
Khi quay nửa đường tròn ngoại tiếp hình chữ nhật \(ABCD\) quay quanh đường thẳng \(MN\) với \(M\) là trung điểm \(AD\) , \(N\) là trung điểm \(BC\) ta được một hình cầu tâm \(O\) bán kính $R = \dfrac{5}{2}$
Diện tích mặt cầu là \(S = 4\pi {R^2} = 4.\pi {\left( {\dfrac{5}{2}} \right)^2} = 25\pi \) \(\left( {cm} \right)\) .
Hướng dẫn giải:
Công thức diện tích mặt cầu $S = 4\pi {R^2}$
Giải thích thêm:
Một số em có thể nhớ nhầm công thức diện tích thành \(S = \pi {R^2}\) dẫn đến ra kết quả D sai .
Một số em có thể quên số \(\pi \) trong công thức diện tích dẫn đến kết quả C sai.
