Kết quả:
0/40
Thời gian làm bài: 00:00:00
Số đo cung lớn \(BnC\) trong hình bên là:

Số giao điểm của đường thẳng $d:y = 2x + 4$ và parabol $\left( P \right):y = {x^2}$ là:
Hai đường thẳng $d:y = ax + b\,\,\left( {a \ne 0} \right)$ và $d':y = a'x + b'\,\,\left( {a' \ne 0} \right)$ có $a = a'$ và $b \ne b'$. Khi đó
Đồ thị hàm số $y = 3\left( {x - 1} \right) + \dfrac{4}{3}$ đi qua điểm nào dưới đây?
Chọn phát biểu đúng. Phương trình $a{x^2} + bx + c = 0\,\,(a \ne 0)$ có hai nghiệm ${x_1};{x_2}$. Khi đó
Cho đường tròn \(\left( {O;R} \right)\) và một điểm \(M\) bên trong đường tròn đó. Qua \(M\) kẻ hai dây cung \(AB\) và \(CD\) vuông góc với nhau (\(C\) thuộc cung nhỏ \(AB\)). Vẽ đường kính \(DE.\) Khi đó tứ giác \(ABEC\) là:
Đường thẳng và đường tròn có nhiều nhất bao nhiêu điểm chung
Với \(m = 1\) thì hệ phương trình: \(\left\{ \begin{array}{l}x - y = m + 1\\x + 2y = 2m + 3\end{array} \right.\) có cặp nghiệm \((x;y)\) là:
Tìm $m$ để đường thẳng $\left( d \right):{\rm{ }}y = x + 3;\left( {d'} \right):{\rm{ }}y = - x + 1;\left( {d''} \right):{\rm{ }}y = \sqrt 3 x - m - 2$ đồng quy.
Nếu hai đường tròn tiếp xúc với nhau thì số điểm chung của hai đường tròn là
Với giá trị nào của \(m\) thì hệ phương trình: \(\left\{ \begin{array}{l}mx + y = 2m\\x + my = m + 1\end{array} \right.\) có vô số nghiệm.
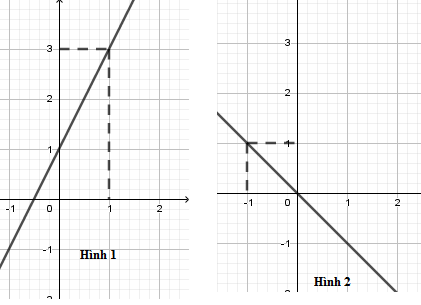
Trong các hình vẽ sau, hình vẽ nào là đồ thị hàm số $y = 2x + 1$
Gọi ${x_1};{x_2}$ là nghiệm của phương trình ${x^2} - 5x + 2 = 0$. Không giải phương trình, tính giá trị của biểu thức $A = x_1^2 + x_2^2$
Cho tam giác \(ABC\) cân tại \(A\) nội tiếp đường tròn tâm \(O.\) Trên \(\left( O \right)\) lấy điểm \(D\) thuộc cung \(AC\). Gọi \(E = AC \cap BD,\,\,F = AD \cap BC.\) Khi đó mệnh đề đúng là:
Cho $3$ đường thẳng $\left( d \right):{\rm{ }}y = \left( {m + 2} \right)x - 3m;\left( {d'} \right):{\rm{ }}y = 2x + 4\;;\left( {d''} \right):{\rm{ }}y = - 3x - 1.$ Giá trị của $m$ để $3$ đường thẳng trên đồng quy là :
Cho hai đường tròn $\left( {O;8\,cm} \right)$ và $\left( {O';6cm} \right)$ cắt nhau tại $A,B$ sao cho $OA$ là tiếp tuyến của $\left( {O'} \right)$. Độ dài dây $AB$ là
Một cột đèn có bóng trên mặt đất dài $7,5m.$ Các tia nắng mặt trời tạo với mặt đất một góc xấp xỉ bằng ${42^0}.$ Tính chiều cao của cột đèn. (làm tròn đến chữ số thập phân thứ ba)
Cho đường tròn $\left( O \right)$ đường kính $AB = $ \(4\sqrt 3 \) $cm$ .
Điểm \(C \in (O)\) sao cho \(\widehat {ABC} = {30^0}\). Tính diện tích hình viên phân$AC$ . (Hình viên phân là phần hình tròn giới hạn bởi một cung tròn và dây căng cung ấy).
Số nghiệm của hệ phương trình sau: \(\left\{ \begin{array}{l}\left| x \right| + 4\left| y \right| = 18\\3\left| x \right| + \left| y \right| = 10\end{array} \right.\) là:
Cho biểu thức \(P = \dfrac{{2x}}{{\sqrt x + 1}}\). Giá trị của $P$ khi $x = 9$ là
Cho biểu thức \(P = \dfrac{{\sqrt x + 1}}{{\sqrt x - 2}}\).
Giá trị của $P$ khi $x = 3 + 2\sqrt 2 $ là:
Cho biểu thức $P = \left( {\dfrac{{\sqrt x + 1}}{{x - 9}} - \dfrac{1}{{\sqrt x + 3}}} \right)\left( {\sqrt x - 3} \right)$. Rút gọn \(P\) .
Rút gọn biểu thức: $A = \left( {\dfrac{{\sqrt x }}{2} - \dfrac{1}{{2\sqrt x }}} \right)\left( {\dfrac{{x - \sqrt x }}{{\sqrt x + 1}} - \dfrac{{x + \sqrt x }}{{\sqrt x - 1}}} \right)$ v ới \(x > 0;\,\,x \ne 1.\)
Cho hàm số $y = mx - 2$ có đồ thị là đường thẳng ${d_1}$ và hàm số $y = \dfrac{1}{2}x + 1$ có đồ thị là đường thẳng ${d_2}$. Xác định $m$ để hai đường thẳng ${d_1}$ và ${d_2}$ cắt nhau tại một điểm có hoành độ $x = - 4$.
Cho đường thẳng $d':y = - 2x + 6$. Gọi $M,N$ lần lượt là giao điểm của $d'$ với $Ox$ và $Oy$. Khi đó chu vi tam giác $OMN$ là:
Hai công nhân cùng làm 1 công việc. Công nhân thứ nhất làm được $1,5$ ngày thì công nhân thứ 2 đến làm cùng và sau $5,5$ ngày nữa là xong công việc. Biết rằng người thứ 2 hoàn thành công việc đó một mình nhanh hơn người thứ nhất là $3$ ngày. Hỏi nếu làm một mình thì thời gian làm xong công việc của người thứ nhất và người thứ hai lần lượt là:
Có 2 loại quặng chứa 75% sắt và 50% sắt. Tính khối lượng quặng chứa 75% sắt đem trộn với quặng chứa 50% sắt để được $25$ tấn quặng chứa 66% sắt.
Giá trị nào dưới đây gần nhất với giá trị của \(m\)để phương trình \({x^2} + 3x - m = 0\) có hai nghiệm \({x_1},{x_2}\) thỏa mãn: \(2{x_1} + 3{x_2} = 13\).
Phương trình \(\dfrac{{2x}}{{x - 2}} - \dfrac{5}{{x - 3}} = \dfrac{{ - 9}}{{{x^2} - 5x + 6}}\)có số nghiệm là
Phương trình \(\dfrac{x}{{\sqrt {4x - 1} }} + \dfrac{{\sqrt {4x - 1} }}{x} = 2\) có bao nhiêu nghiệm?
Một thửa ruộng hình tam giác có diện tích \(180\,{m^2}\). Tính chiều dài cạnh đáy thửa ruộng, biết rằng nếu tăng cạnh đáy lên $4m$ và chiều cao tương ứng giảm đi $1\,\,m$ thì diện tích không đổi.
Một ca nô chạy xuôi dòng với quãng đường $42{\rm{km}}$, rồi sau đó ngược dòng trở lại $20{\rm{ km}}$ hết tổng cộng $5{\rm{h}}$. Biến vận tốc của dòng nước chảy là $2{\rm{ km/h}}$. Tính vận tốc của ca nô lúc dòng nước yên lặng.
Một lâm trường dự định trồng $75$ $ha$ rừng trong một số tuần (mỗi tuần trồng được diện tích bằng nhau). Thực tế, mỗi tuần lâm trường trồng vượt mức $5$ $ha$ so với dự định nên cuối cùng đã trồng được $80$ $ha$ và hoàn thành sớm hơn dự định một tuần. Hỏi mỗi tuần lâm trường dự định trồng bao nhiêu $ha$ rừng?
Cho $a,b$ là hai đường thẳng song song và cách nhau một khoảng $2,5\,cm$. Lấy điểm $I$ trên $a$ và vẽ đường tròn $\left( {I;2,5cm} \right)$. Khi đó đường tròn với đường thẳng $b$
Cho tam giác nhọn \(ABC\) nội tiếp \(\left( O \right)\) . Kẻ tiếp tuyến \(xAy\) với \(\left( O \right)\) . Từ \(B\) kẻ \(BM{\rm{//}}xy\left( {M \in AC} \right)\) . Khi đó tích $AM.AC$ bằng
Cho điểm \(C\) thuộc nửa đường tròn \(\left( O \right)\) đường kính \(AB.\) Từ điểm \(D\) thuộc đọan \(AO\) kẻ đường thẳng vuông góc với \(AO\) cắt \(AC\) và \(BC\) lần lượt lại \(E\) và \(F.\) Tiếp tuyến tại \(C\) với nửa đường tròn cắt $EF$ tại \(M\) và cắt \(AB\) tại \(N.\) Khi đó
Cho một hình trụ, một hình nón và một hình cầu có thể tích bằng nhau. Bán kính đáy của hình trụ, bán kính đáy của hình nón và bán kính của hình cầu đều bằng $R.$ Tính các chiều cao \({h_1}\) của hình trụ và \({h_2}\) của hình nón theo \(R.\)
Cho \(A = \dfrac{{2x}}{{x + 3\sqrt x + 2}} + \dfrac{{5\sqrt x + 1}}{{x + 4\sqrt x + 3}} + \dfrac{{\sqrt x + 10}}{{x + 5\sqrt x + 6}}\) với \(x \ge 0\). Chọn đáp án đúng.
Cho \(A\) là điểm cố định trên đường tròn \(\left( {O;R} \right).\) Gọi \(AB\) và \(AC\) là hai dây cung thay đổi trên đường tròn \(\left( O \right)\) thỏa mãn \(\sqrt {AB.AC} = R\sqrt 3 .\) Khi đó vị trí của \(B,\,C\) trên \(\left( O \right)\) để diện tích \(\Delta ABC\) lớn nhất là:
Cho $M\left( {0;2} \right),N\left( {1;0} \right),P\left( { - 1; - 1} \right)$ lần lượt là trung điểm của các cạnh $BC,CA$ và $AB$ của tam giác $ABC$ . Viết phương trình đường trung trực của đoạn thẳng $AB$.

