Trả lời bởi giáo viên
Đáp án đúng: c
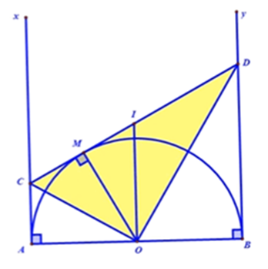
Theo tính chất hai tiếp tuyến cắt nhau: AC=CM và BD=DM
Chu vi hình thang ABDC là:
PABDC=AC+AB+BD+CD=CM+AB+DM+CD=AB+2CD
⇒PABDCmin
Mà OM\; \bot CD{\rm{ }} \Rightarrow OM\; \bot AB
\Rightarrow {P_{ABDC\min }} = AB + 2AB = 3AB
Vậy chu vi nhỏ nhất của hình thang ABDC là 3AB khi OM \bot AB .
Hướng dẫn giải:
Sử dụng tính chất hai tiếp tuyến cắt nhau
Sử dụng công thức tính chu vi hình thang và lập luận để có chu vi nhỏ nhất