Câu hỏi:
2 năm trước
Cho hai đường tròn $\left( O \right);\left( {O'} \right)$ cắt nhau tại $A,B$, trong đó $O' \in \left( O \right)$. Kẻ đường kính $O'OC$ của đường tròn $\left( O \right)$. Chọn khẳng định sai?
Trả lời bởi giáo viên
Đáp án đúng: d
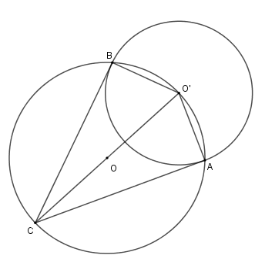
Xét đường tròn $\left( O \right)$ có $O'C$ là đường kính, suy ra $\widehat {CBO'} = \widehat {CAO'} = 90^\circ $ hay $CB \bot O'B$ tại $B$ và $AC \bot AO'$ tại $A$.
Do đó $AB,BC$ là hai tiếp tuyến của $\left( {O'} \right)$ nên $AC = CB$ (tính chất hai tiếp tuyến cắt nhau)
Nên A, B, C đúng.
Hướng dẫn giải:
Sử dụng cách chứng minh một đường thẳng là tiếp tuyến của đường tròn.