Câu hỏi:
2 năm trước
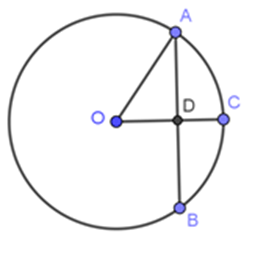
Cho tam giác $ABC$ vuông tại $A$, đường cao $AH$. Đường tròn đường kính $BH$ cắt $AB$ tại $D$, đường tròn đường kính $CH$ cắt $AC$ tại $E$ . Chọn khẳng định sai trong các khẳng định sau
Trả lời bởi giáo viên
Đáp án đúng: a
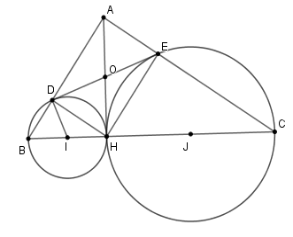
Gọi $I$, $J$ lần lượt là trung điểm của $BH$ và $CH.$
Để chứng minh $DE$ là tiếp tuyến của đường tròn tâm $I$ đường kính $BH$ ta chứng minh
\(ID \bot DE\) hay $\widehat {ODI} = {90^o}$
Vì $D,E$ lần lượt thuộc đường tròn đường kính $BH$ và $HC$ nên ta có: $\widehat {BDH} = \widehat {CEH} = {90^0}$
Suy ra tứ giác $ADHE$ là hình chữ nhật.
Gọi $O$ là giao điểm của $AH$ và$DE$, khi đó ta có $OD = OH = OE = OA$ .
Suy ra $\Delta ODH$ cân tại $O \Rightarrow \widehat {ODH} = \widehat {OHD}$
Ta cũng có $\Delta IDH$ cân tại $I$$ \Rightarrow \widehat {IDH} = \widehat {IHD}$
Từ đó $ \Rightarrow \widehat {IDH} + \widehat {HDO} = \widehat {IHD} + \widehat {DHO} \Rightarrow \widehat {IDO} = 90^\circ $$ \Rightarrow ID \bot DE$
Ta có \(ID \bot DE,D \in \left( I \right)\) nên $DE$ là tiếp tuyến của đường tròn đường kính $BH$.
Từ chứng minh trên suy ra các phương án B,C,D đúng.
Hướng dẫn giải:
Sử dụng dấu hiệu nhận biết các hình đặc biệt và cách chứng minh một đường thẳng là tiếp tuyến của đường tròn.
Câu hỏi khác
- Đề kiểm tra 15 phút chương 6: đường tròn - đề số 2 Toán 9 có lời giải chi tiết
- Đề kiểm tra 15 phút chương 6: đường tròn - đề số 1 Toán 9 có lời giải chi tiết
- Đề kiểm tra 45 phút chương 6: đường tròn - đề số 2 Toán 9 có lời giải chi tiết
- Đề kiểm tra 45 phút chương 6: đường tròn - đề số 1 Toán 9 có lời giải chi tiết
