Cho đường tròn \((O).\) Từ một điểm \(M\) ở ngoài \((O)\), vẽ hai tiếp tuyến \(MA\) và \(MB\) sao cho góc \(AMB\) bằng \({60^0}\). Biết chu vi tam giác \(MAB\) là \(24\,cm\), tính độ dài bán kính đường tròn.
Trả lời bởi giáo viên
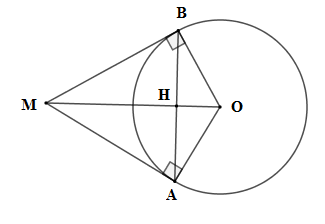
Xét \(\left( O \right)\) có \(MA = MB\) (tính chất hai tiếp tuyến cắt nhau) mà \(\widehat {AMB} = 60^\circ \) nên \(\Delta MAB\) đều suy ra chu vi \(\Delta MAB\) là \(MA + MB + AB = 3AB = 24 \)\(\Rightarrow AB = 8cm = MA = MB\)
Lại có \(\widehat {AMO} = \dfrac{1}{2}\widehat {AMB} = 30^\circ \) (tính chất 2 tiếp tuyến cắt nhau)
Xét tam giác vuông \(MAO\) có \(\tan \widehat {AMO} = \dfrac{{OA}}{{MA}} \Rightarrow OA = MA.\tan 30^\circ = \dfrac {4}{\sqrt 3}\,cm\)
Hướng dẫn giải:
Sử dụng tính chất hai tiếp tuyến cắt nhau và công thức chu vi tam giác
Sử dụng tỉ số lượng giác của góc nhọn