Trả lời bởi giáo viên
Đáp án đúng: b
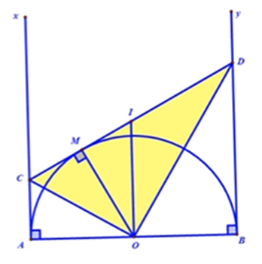
Vì I là trung điểm của CD.
Nên I là tâm của đường tròn đường kính CD.
Theo tính chất hai tiếp tuyến cắt nhau: AC=CM và BD=DM
Xét tứ giác ABDC có: AC//BD⇒ABDC là hình thang
Suy ra IO là đường trung bình của hình thang ABDC
⇒ IO//AC//BD mà AC⊥AB⇒IO⊥AB(1)
IO=AC+BD2=CM+DM2=CD2(2)
Từ (1) và (2) suy ra đường tròn đường kính CD tiếp xúc với AB.
Vậy A,C,D đúng, B sai.
Hướng dẫn giải:
Sử dụng tính chất hai tiếp tuyến cắt nhau và tính chất đường trung bình của hình thang
Sử dụng vị trí tương đối của hai đường tròn