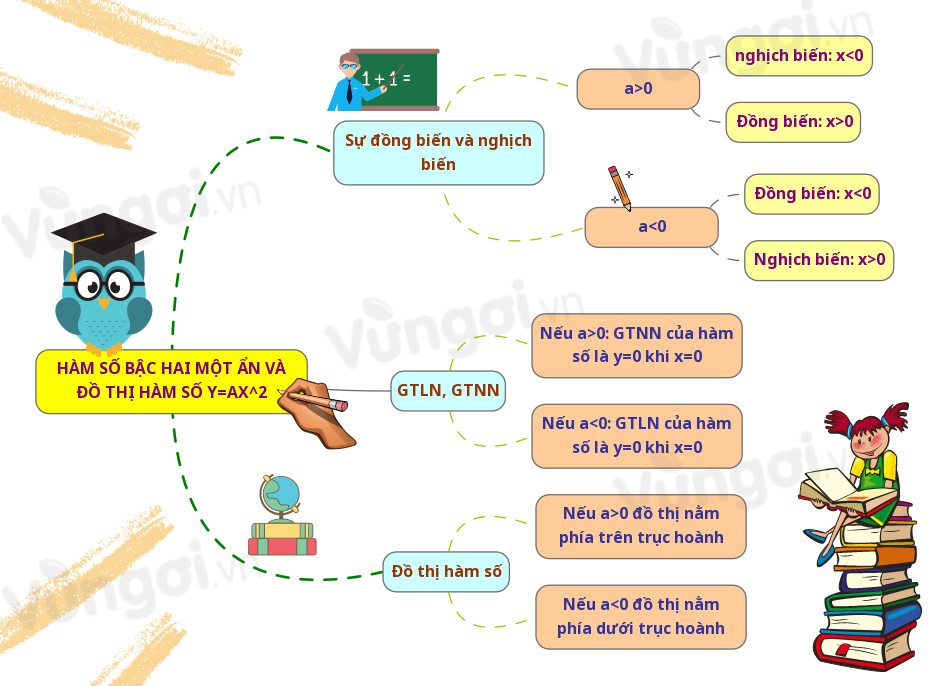
I. Sơ đồ tư duy Hàm số bậc hai một ẩn và đồ thị hàm số y=ax^2
II. Hàm số bậc hai một ẩn và đồ thị hàm số y=ax^2
1. Các kiến thức cần nhớ
Sự đồng biến và nghịch biến của hàm số $y = a{x^2}\,\,\left( {a \ne 0} \right)$
+) Nếu \(a > 0\) thì hàm số nghịch biến khi \(x < 0\) và đồng biến khi \(x > 0\).
+) Nếu \(a < 0\) thì hàm số đồng biến khi \(x < 0\) và nghịch biến khi \(x > 0\).
+) Nếu $a > 0$ thì $y > 0$ với mọi $x \ne 0$;
$y = 0$ khi $x = 0$ và giá trị nhỏ nhất của hàm số là $y = 0$.
+) Nếu $a < 0$ thì $y < 0$ với mọi $x \ne 0$;
$y = 0$ khi $x = 0$ và giá trị lớn nhất của hàm số là $y = 0$.
Đồ thị hàm số $y = a{x^2}\,\,\left( {a \ne 0} \right)$
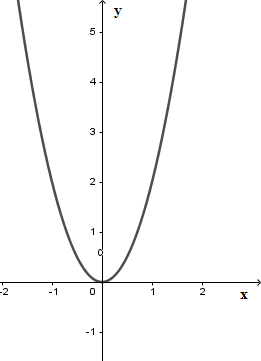
Đồ thị của hàm số $y = a{x^2}\,\,\left( {a \ne 0} \right)$ là một đường cong đi qua gốc tọa độ $O$ và nhận trục $Oy$ làm trục đối xứng.
Đường cong đó là một parabol với đỉnh $O$.
- Nếu \(a > 0\) thì đồ thị nằm phía trên trục hoành, $O$ là điểm thấp nhất của đồ thị.
- Nếu \(a < 0\) thì đồ thị nằm phía dưới trục hoành, $O$ là điểm cao nhất của đồ thị.
2. Các dạng toán thường gặp
Dạng 1: Tính giá trị của hàm số tại một điểm cho trước
Phương pháp:
Giá trị của hàm số \(y = a{x^2}\left( {a \ne 0} \right)\) tại điểm \(x = {x_0}\) là ${y_0} = ax_0^2$.
Dạng 2: Bài toán liên quan đến tính đồng biến và nghịch biến của hàm số
Phương pháp:
Xét hàm số \(y = a{x^2}\left( {a \ne 0} \right).\) Ta có:
- Nếu \(a > 0\) thì hàm số nghịch biến khi \(x < 0\) và đồng biến khi \(x > 0\).
- Nếu \(a < 0\) thì hàm số đồng biến khi \(x < 0\) và nghịch biến khi \(x > 0\).
Dạng 3: Các bài toán liên quan đến đồ thị hàm số \(y = a{x^2}\left( {a \ne 0} \right)\)
Phương pháp:
Để vẽ đồ thị hàm số \(y = a{x^2}\left( {a \ne 0} \right)\) ta thực hiện các bước sau
Bước 1: Lập bảng giá trị đặc biệt tương ứng giữa $x$ và $y$ của hàm số $y = a{x^2}\,\,(a \ne 0)$.
Thông thường ta sẽ lấy ít nhất 5 giá trị của $x$ là $-2;-1;0;1;2$ rồi tính lần lượt từng giá trị của $y$ tương ứng. Tuy nhiên ta cần linh hoạt trong cách lấy để thu được kết quả dễ xác định nhất.
Bước 2: Biểu diễn các điểm đặc biệt trên mặt phẳng tọa độ và vẽ đồ thị dạng parabol của hàm số đi qua các điểm đặc biệt đó.
Dạng 4: Tọa độ giao điểm của parabol và đường thẳng
Phương pháp:
Cho parabol $(P):y=a{x^2}(a \ne 0)$ và đường thẳng $d:y = mx + n$. Để tìm tọa độ giao điểm (nếu có) của $(d)$ và $(P)$, ta làm như sau:
Bước 1. Xét phương trình hoành độ giao điểm của $(d)$ và $(P)$: $a{x^2} = mx + n$ (*)
Bước 2. Giải phương trình (*) ta tìm được nghiệm (nếu có). Từ đó ta tìm được tọa độ giao điểm của $(d)$ và $(P)$ .
Số nghiệm của (*) bằng đúng số giao điểm của đường thẳng $d$ và parabol $P$.
- Nếu (*) vô nghiệm thì $(d)$ không cắt $(P)$;
- Nếu (*) có nghiệm kép thì $(d)$ tiếp xúc với $(P)$;
- Nếu (*) có $2$ nghiệm phân biệt thì $(d)$ cắt $(P)$ tại hai điểm phân biệt.