I. Sơ đồ tư duy Phương trình bậc hai một ẩn và công thức nghiệm
II. Phương trình bậc hai một ẩn và công thức nghiệm
1. Các kiến thức cần nhớ
Định nghĩa phương trình bậc hai một ẩn
- Phương trình bậc hai một ẩn ( hay gọi tắt là phương trình bậc hai) là phương trình có dạng: $a{x^2} + bx + c = 0\,\,(a \ne 0)$
Trong đó $a,b,c$ là các số thực cho trước, $x$ là ẩn số.
- Giải phương trình bậc hai một ẩn là đi tìm tập nghiệm của phương trình bậc hai một ẩn đó.
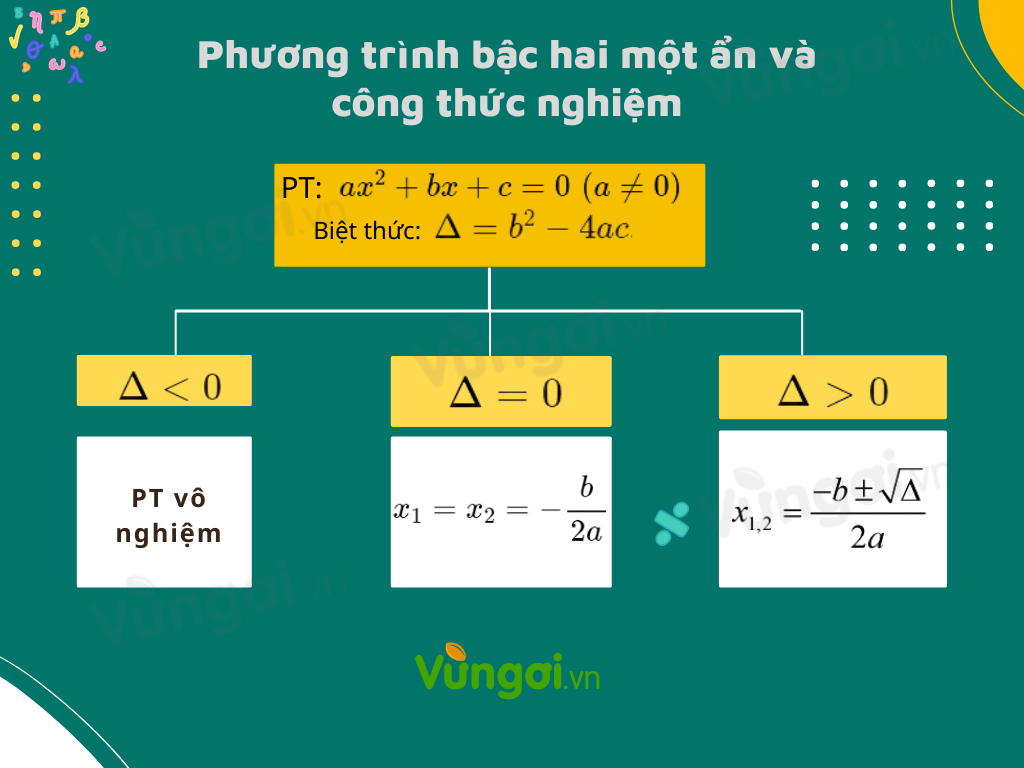
Công thức nghiệm của phương trình $a{x^2} + bx + c = 0\,\,(a \ne 0)$
Xét phương trình bậc hai một ẩn $a{x^2} + bx + c = 0\,\,(a \ne 0)$
và biệt thức $\Delta = {b^2} - 4ac$.
TH1. Nếu $\Delta < 0$ thì phương trình vô nghiệm.
TH2. Nếu $\Delta = 0$ thì phương trình có nghiệm kép: ${x_1} = {x_2} = - \dfrac{b}{{2a}}$.
TH3. Nếu $\Delta > 0$ thì phương trình có hai nghiệm phân biệt: ${x_{1}} = \dfrac{{ - b + \sqrt \Delta }}{{2a}}$, ${x_{2}} = \dfrac{{ - b - \sqrt \Delta }}{{2a}}$.
2. Các dạng toán thường gặp
Dạng 1: Nhận dạng phương trình bậc hai một ẩn
Phương pháp:
Phương trình bậc hai một ẩn ( hay gọi tắt là phương trình bậc hai) là phương trình có dạng:
$a{x^2} + bx + c = 0\,\,(a \ne 0)$ trong đó $a,b,c$ là các số thực cho trước, $x$ là ẩn số.
Dạng 2: Giải phương trình bậc hai một ẩn không dùng công thức nghiệm
Phương pháp:
Ta thường sử dụng các cách sau:
Cách 1: Đưa phương trình đã cho về dạng vế trái là một bình phương, vế còn lại là một số hoặc một bình phương.
Cách 2: Đưa phương trình về dạng phương trình tích.
Dạng 3: Giải phương trình bậc hai một ẩn bằng cách sử dụng công thức nghiệm.
Phương pháp:
Xét phương trình bậc hai: $a{x^2} + bx + c = 0\,\,(a \ne 0)$
Bước 1: Xác định các hệ số $a,b,c$ và tính biệt thức $\Delta = {b^2} - 4ac$
Bước 2: Kết luận
- Nếu $\Delta < 0$ thì phương trình vô nghiệm.
- Nếu $\Delta = 0$ thì phương trình có nghiệm kép: ${x_1} = {x_2} = - \dfrac{b}{a}$
- Nếu $\Delta > 0$ thì phương trình có hai nghiệm phân biệt: ${x_1} = \dfrac{{ - b + \sqrt \Delta }}{{2a}};{x_2} = \dfrac{{ - b - \sqrt \Delta }}{{2a}}$.
Dạng 4: Xác định số nghiệm của phương trình bậc hai
Phương pháp:
Xét phương trình bậc hai: $a{x^2} + bx + c = 0\,\,(a \ne 0)$
1. PT có nghiệm kép $ \Leftrightarrow \left\{ \begin{array}{l}a \ne 0\\\Delta = 0\end{array} \right.$
2. PT có hai nghiệm phân biệt $ \Leftrightarrow \left\{ \begin{array}{l}a \ne 0\\\Delta > 0\end{array} \right.$
3. PT vô nghiệm $ \Leftrightarrow a \ne 0;\,\Delta < 0$.

