I. Sơ đồ tư duy Hệ phương trình bậc nhất hai ẩn chứa tham số
II. Hệ phương trình bậc nhất hai ẩn chứa tham số
1. Các kiến thức cần nhớ
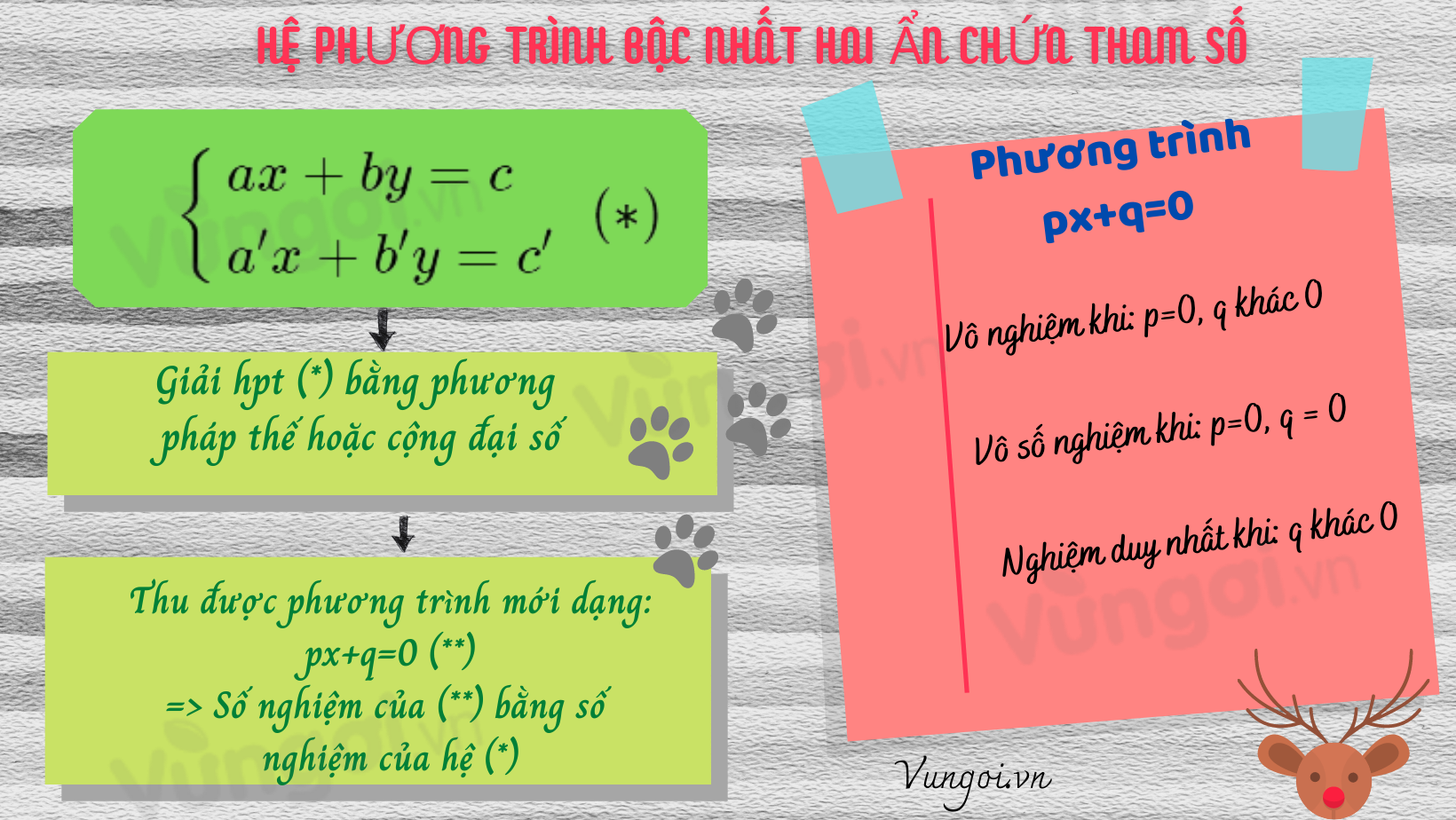
Cho hệ phương trình bậc nhất hai ẩn $\left\{ \begin{array}{l}ax + by = c\\a'x + b'y = c'\end{array} \right.{\rm{ }}\left( * \right)$
a. Để giải hệ phương trình \(\left( * \right)\), ta thường dùng phương pháp thế hoặc phương pháp cộng đại số.
b. Từ hai phương trình của hệ phương trình \(\left( * \right)\), sau khi dùng phương pháp thế và phương pháp cộng đại số ta thu được một phương trình mới một ẩn (thông thường đưa về dạng $px + q = 0$).
Số nghiệm của phương trình mới thu được chính là số nghiệm của hệ phương trình đã cho.
Phương trình $ax + b = 0$
+) Vô nghiệm khi $a = 0;b \ne 0$
+) Vô số nghiệm khi $a = 0;b = 0$
+) Có nghiệm duy nhất khi $a \ne 0$
2. Các dạng toán thường gặp
Dạng 1: Giải và biện luận hệ phương trình
Phương pháp:
Cho hệ phương trình $\left\{ \begin{array}{l}ax + by = c\\a'x + b'y = c'\end{array} \right.{\rm{ }}\left( * \right)$
Để giải và biện luận hệ phương trình $\left( * \right)$, ta thực hiện các bước sau:
Bước 1. Từ hai phương trình của \(\left( * \right)\), sau khi dùng phương pháp thế hoặc cộng đại số, ta thu được một phương trình mới ( chỉ còn một ẩn).
Bước 2. Giải và biện luận hệ phương trình mới, từ đó đi đến kết luận về giải và biện luận hệ phương trình đã cho.
Dạng 2: Tìm điều kiện của tham số để hệ phương trình thỏa mãn điều kiện cho trước
Phương pháp:
Bài toán 1: Tìm điều kiện của tham số để hệ phương trình có nghiệm duy nhất thỏa mãn điều kiện cho trước
Bài toán 2: Tìm điều kiện của tham số để hệ phương trình có nghiệm nguyên.
Dạng 3: Tìm mối liên hệ giữa $x,y$ không phụ thuộc vào tham số $m$
Phương pháp:
Bước 1: Giải hệ phương trình tìm được nghiệm $\left( {x,y} \right)$ theo tham số $m$
Bước 2: Dùng phương pháp cộng đại số hoặc phương pháp thế làm mất tham số \(m\) và kết luận.
