Từ một điểm A ở bên ngoài đường tròn (O) ta vẽ hai tiếp tuyến AB, AC với đường tròn (B, C là các tiếp điểm). Trên AO lấy điểm M sao cho \(AM = AB.\) Các tia BM và CM lần lượt cắt đường tròn tại một điểm thứ hai là D và E. Chọn câu đúng.
Trả lời bởi giáo viên
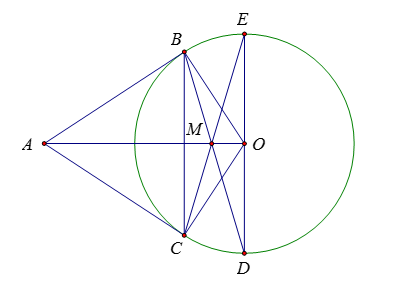
Tam giác ABM có \(AB = AM\) nên ΔABM cân tại A \( \Rightarrow \widehat {ABM} = \widehat {AMB}\,\,\left( 1 \right)\)
Ta có: \(OA ⊥ BC; OB ⊥ AB\) nên: \(\left\{ \begin{array}{l}\widehat {ABM} + \widehat {MBO} = 90^\circ \\\widehat {AMB} + \widehat {MBC} = 90^\circ \end{array} \right.\,\left( 2 \right)\)
Từ (1) và (2) \( \Rightarrow \widehat {MBO} = \widehat {MBC}\)
Tương tự \(\widehat {BCM} = \widehat {OCM}\)
Điểm M là giao điểm hai đường phân giác của tam giác OBC nên M là tâm đường tròn nội tiếp tam giác OBC.
Vì tam giác BOD cân tại O \( \Rightarrow \widehat {MBO} = \widehat {MDO}\) mà \(\widehat {MBO} = \widehat {MBC}\) nên \(\widehat {MBC} = \widehat {MDO}\)
Mà hai góc này ở vị trí so le trong nên \(OD // BC\)
Chứng minh tương tự, ta có \(OE // BC\)
\( \Rightarrow D,{\rm{ }}O,{\rm{ }}E\) thẳng hàng
Vậy DE là đường kính của đường tròn (O)
Hướng dẫn giải:
Sử dụng:
Tâm đường tròn ngoại tiếp tam giác là giao ba đường trung trực
Tâm đường tròn nội tiếp tam giác là giao ba đường phân giác góc trong
Nếu \(AB//d;\,AC//d\) thì \(A,B,C\) thẳng hàng.


