Bài tập cuối tuần Toán lớp 8 – Tuần 7

TUẦN 7 – PHÂN TÍCH ĐA THỨC THÀNH NHÂN TỬ ( TIẾP )

ĐỐI XỨNG TÂM

Bài 1: Phân tích các đa thức sau thành nhân tử:

$a) a^2-10a+25-4b^2;$

$b) a\left(x^2+1\right)-x\left(a^2+1\right);$

$c) m^{3}p+m^{2}np-$$m^2{p}^2-mn{p}^2;$

$d) ab\left(m^2+n^2\right)+$$mn\left(a^2+b^2\right).$

Bài 2: Phân tích các đa thức sau thành nhân tử:

$a) {\left(xy+ab\right)}^2+{\left(ay-bx\right)}^2;$

$b) m^2\left(n-p\right)+n^2\left(p-m\right)+$$p^2\left(m-n\right);$

$c) x^2-\left(m+n\right)x+mn;$

$d) ax+by+a-$$bx-ay-b.$

Bài 3: Tìm y, biết:

$a) y\left(2y-7\right)-4y+14=0;$

$b) \left(y+3\right)\left(y^2-3y+9\right)-$$y\left(y^2-3\right)=18;$

$c) \left(y^3-y^2\right)-4y^2+$$8y-4=0.$

Bài 4:Tính:

$M=x^{2013}-10x^{2012}+10x^{2011}+\dots -$$10x^2+10x-10$ với x = 9.

Bài 5: Tìm y để giá trị của biểu thức $1+4y-y^2$ là lớn nhất.

Bài 6: Vẽ hình đối xứng với các hình sau qua O.

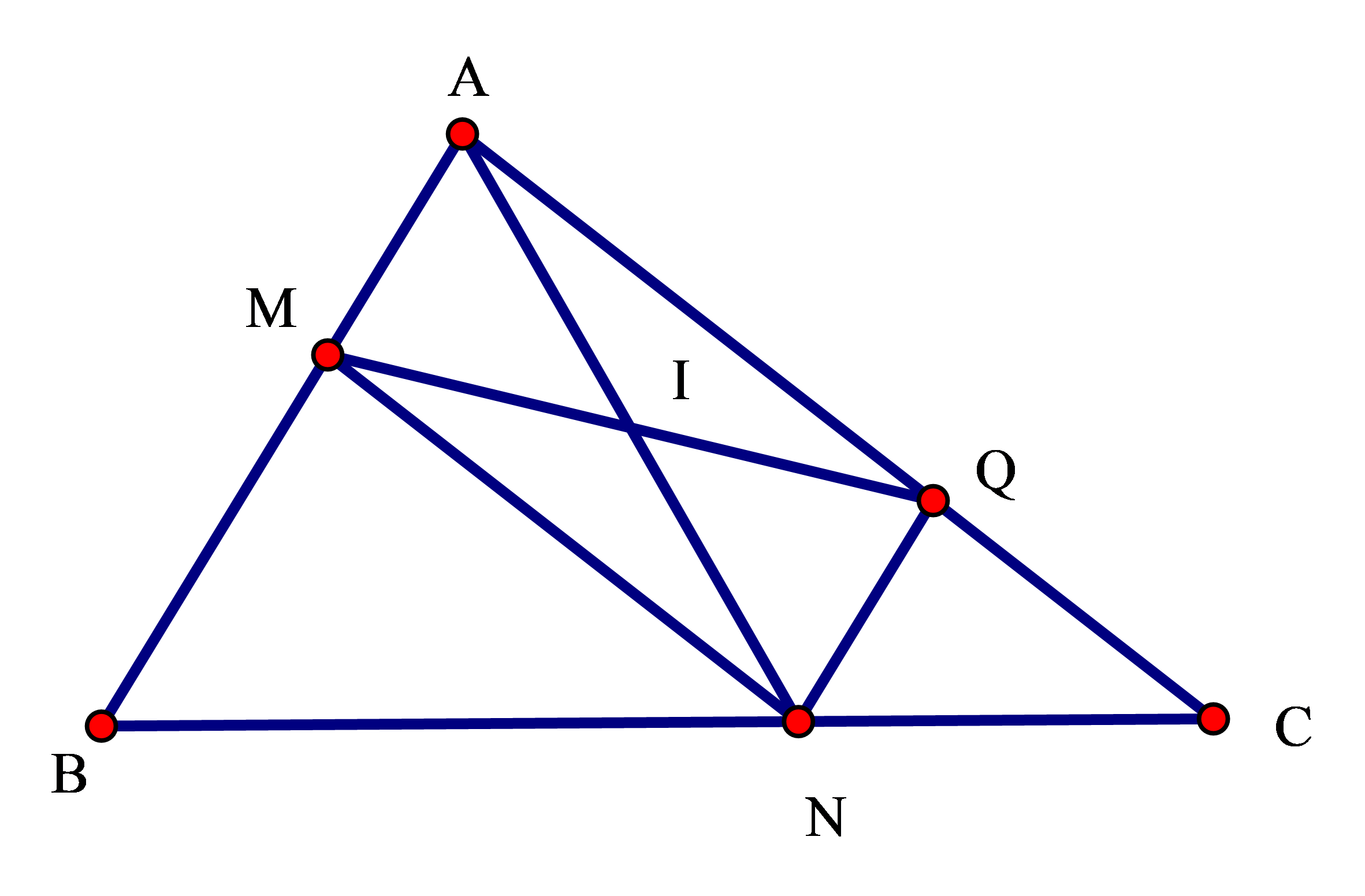
Bài 7: Cho hình vẽ 11, trong đó NQ//AB, MN//AC. I là trung điểm của MQ. Chứng minh N đối xứng với A qua I.

Bài 8: Cho tam giác ABC, trực tâm H, M là trung điểm của BC, O là giao điểm của các đường trung trực. Điểm D đối xứng với H qua M

a) Tứ giác BHCD là hình gì?

b) Chứng minh $\widehat{ABD}=\widehat{ACD}={90}^o$

c)  Chứng minh A và D đối xứng nhau qua O

Bài 9: Cho hình bình hành ABCD, O là giao điểm của hai đường chéo. Trên AB lấy điểm E, trên CD lấy điểm F sao cho AE= CF.

a)  Chứng minh F là điểm đối xứng với E qua O

b) Từ E dựng Ex//AC cắt BC tại I, dựng Fy//AC cắt AD tại K. Chứng minh I và K đối xứng qua O.

Bài 10: Cho tam giác ABC có đường cao AH. Kẻ $HE\perp AB$$\left(E\in AB\right)$, kéo dài HE lấy EM=EH. Kẻ =$HF\perp AC\left(F\in AC\right)$ kéo dài HF lấy FN = FH. Gọi I là trung điểm MN. Chứng minh:

a) AB là trung trực của MH và AC là trung trực của HN

b) Tam giác AMN cân

c) EF// MN

d)  $AI\perp EF$