Bài tập cuối tuần Toán lớp 8 - Tuần 19

TUẦN 19 - ÔN TẬP HỌC KÌ I

Bài 1: Rút gọn biểu thức sau:

$a) \left(x-3\right)\left(x+7\right)-\left(x+5\right)\left(x-1\right)$         

$b) \left(a+1\right)\left(a^2-a+1\right)-\left(a-1\right)\left(a^2+a+1\right)$

$c) \left(17m^2-6m^4+5m^3-23m+7\right):$$\left(7-3m^2-2m\right)$              

Bài 2: Thực hiện phép tính:

$a)\frac{2x+4}{4x^2-x}:\frac{x^2+2x}{1-4x}$

$b)\frac{4x^2-16x}{1-2x+x^2}:\frac{3x+6}{1-x}$

$c)\left[ \frac{1}{x^2}+\frac{1}{y^2}+\frac{2}{x+y}\left(\frac{1}{x}+\frac{1}{y}\right)\right]:$$\frac{x^3+y^3}{x^2{y}^2}$

Bài 3: Cho biểu thức  

$A=\left(\frac{1}{2-x}+\frac{3x}{x^2-4}-\frac{2}{2+x}\right):\left(\frac{x^2+4}{4-x^2}+1\right)$

a) Tìm điều kiện xác định của A

b) Chứng minh rằng giá trị của biểu thức A không phụ thuộc vào giá trị của biến x thuộc tập xác định của A.

Bài 4: Giải các phương trình sau:

$a) \left(m-\frac{1}{2}\right)\left(m-\frac{3}{4}\right)+$$\left(m-\frac{1}{2}\right)\left(m+\frac{3}{4}\right)=0$

$b) \left|m-2\right|=18-4m$

Bài 5: Cho biểu thức 

$P=\frac{x^3+2x^2-5x-6}{x^2+x-6}.$

a) Tìm điều kiện xác định của P

b) Chứng minh rằng với mọi giá trị của x nguyên thỏa mãn điều kiện xác định thì P nhận giá trị nguyên.

Bài 6: Cho hình thang cân ABCD (AB//CD) . Từ A kẻ tia Ax song song với BC, tia Ax cắt DC ở E.

a) Chứng minh tứ giác ABCE là hình bình hành

b) Kẻ đường cao AH, kéo dài BA về phía A một đoạn AM=HD. Chứng minh AHDM là hình chữ nhật

c) Lấy điểm N đối xứng với A qua điểm H. Chứng minh AEND là hình thoi.

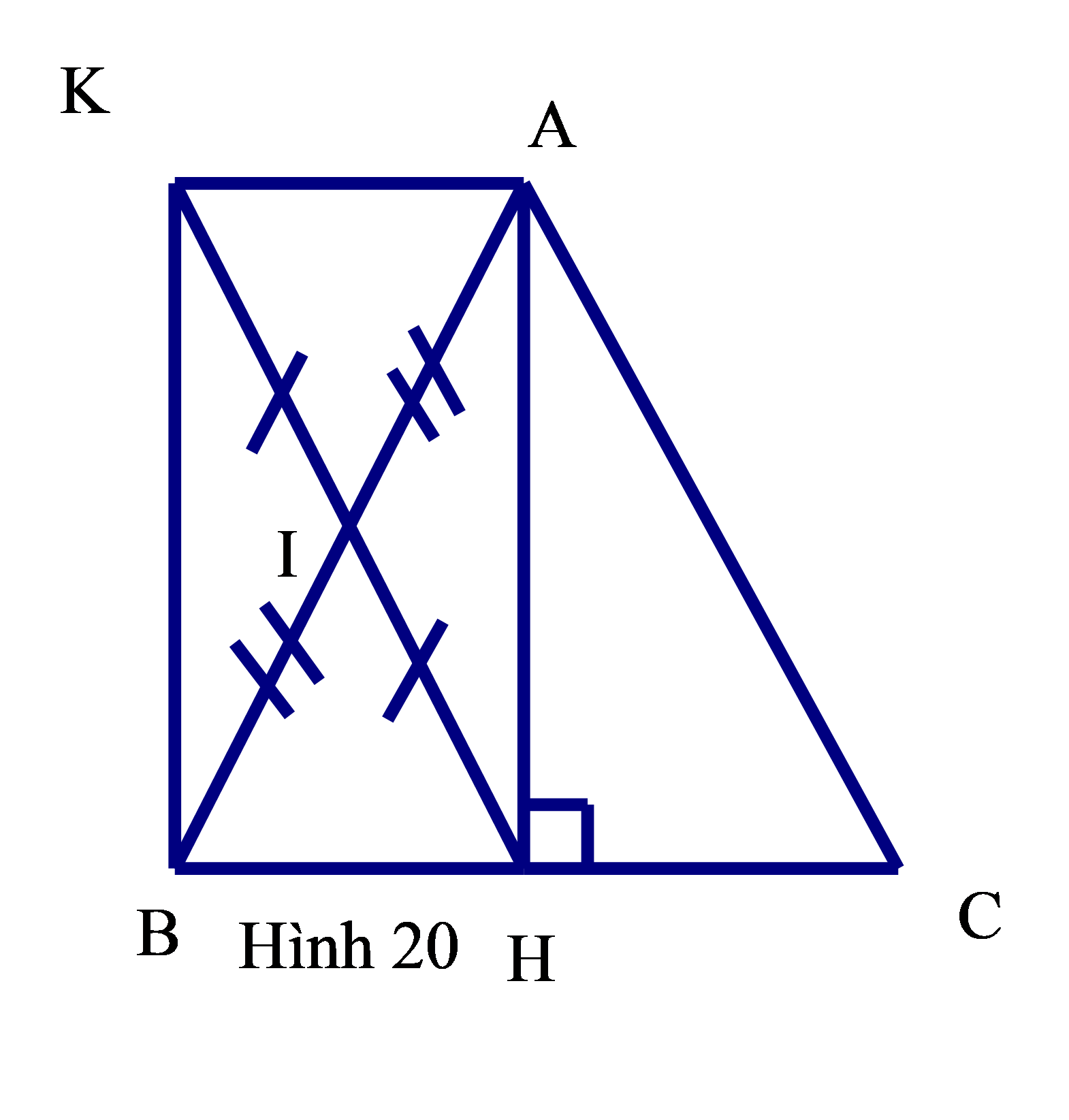
Bài 7: Cho tam giác ABC cân tại A, đường cao AH(hình 20). Gọi I là trung điểm của AB, K là điểm đối xứng của H qua I.

a) Cho biết AB=6cm. Tính IH

b) Chứng minh tứ giác AHBK là hình chữ nhật

c) Tam giác ABC có thêm điều kiện gì thì hình chữ nhật AHBK là hình vuông.

Bài 8: Cho tam giác ABC vuông tại A có đường trung tuyến AM. Kẻ $MH\perp AB, \left(H\in AB\right),$$MK\perp AC\left(K\in AC\right)$.

a) Chứng minh tứ giác AKMH là hình chữ nhật

b) E là trung điểm của MH.Chứng minh ba điểm B, E, K thẳng hàng

c) Gọi F là trung điểmcủa MK. Đường thẳng HK cắt AE tại I và AF tại J. Chứng minh HI=KJ

Bài 9: Cho Cho tứ giác ABCD có AD=AB=BC<CD, hai đường chéo cắt nhau tại O. Gọi M là giao điểm của hai đường thẳng AD và BC. vẽ hình bình hành AMBK. Đường thẳng KO cắt đường thẳng BC tại N. Chứng minh:

a) AC là tia phân giác của góc BAK

b) AM=BN

Bài 10: Cho hình thoi ABCD có F là giao điểm của hai đường chéo. Gọi M là điểm đối xứng với C qua B; N là điểm đối xứng với B qua AM, E là giao điểm của AM và BN.

a) Chứng minh tam giác ACM là một tam giác vuông

b) Chứng minh AEBF là hình chữ nhật và ABMN là hình thoi

c) Chứng minh điểm N đối xứng với điểm D qua A