Bài tập cuối tuần Toán lớp 8 - Tuần 20

TUẦN 20 – PHƯƠNG TRÌNH BẬC NHẤT MỘT ẨN VÀ CÁCH GIẢI

DIỆN TÍCH HÌNH THANG- HÌNH THOI

Bài 1: Giải các phương trình sau:

$a) 2x+6=0$

$b) 2x-3=5$

$c) 5x-3=2$

$d) - 3x + 3 = 9$

Bài 2: Với giá trị nào của m thì các phương trình sau là phương trình bậc nhất?

$a) mx+2=0$

$b) \left(2-m\right)x+2m=0$

$c) m{x}^2-x+5=0$

$d) \left(m-1\right)x^2+mx-8=0$

Bài 3: Giải các phương trình sau:

$a)\frac{1}{4}-2x=0$

$b) 6x-\frac{1}{3}=0$

$c)\frac{x}{7}-5=0$

$d)\frac{x-1}{2}-1=0$

Bài 4: Giải các phương trình sau:

$a) 3\left(3x-\frac{1}{3}\right)=6\left(x+2\right)$

$b) 2x-3=3x+5\left(x+1\right)-5$

Bài 5: Chứng tỏ rằng hai phương trình sau là tương đương:

$2x+10=0 \left(1\right)$ và $3x-2=2x-7 \left(2\right)$

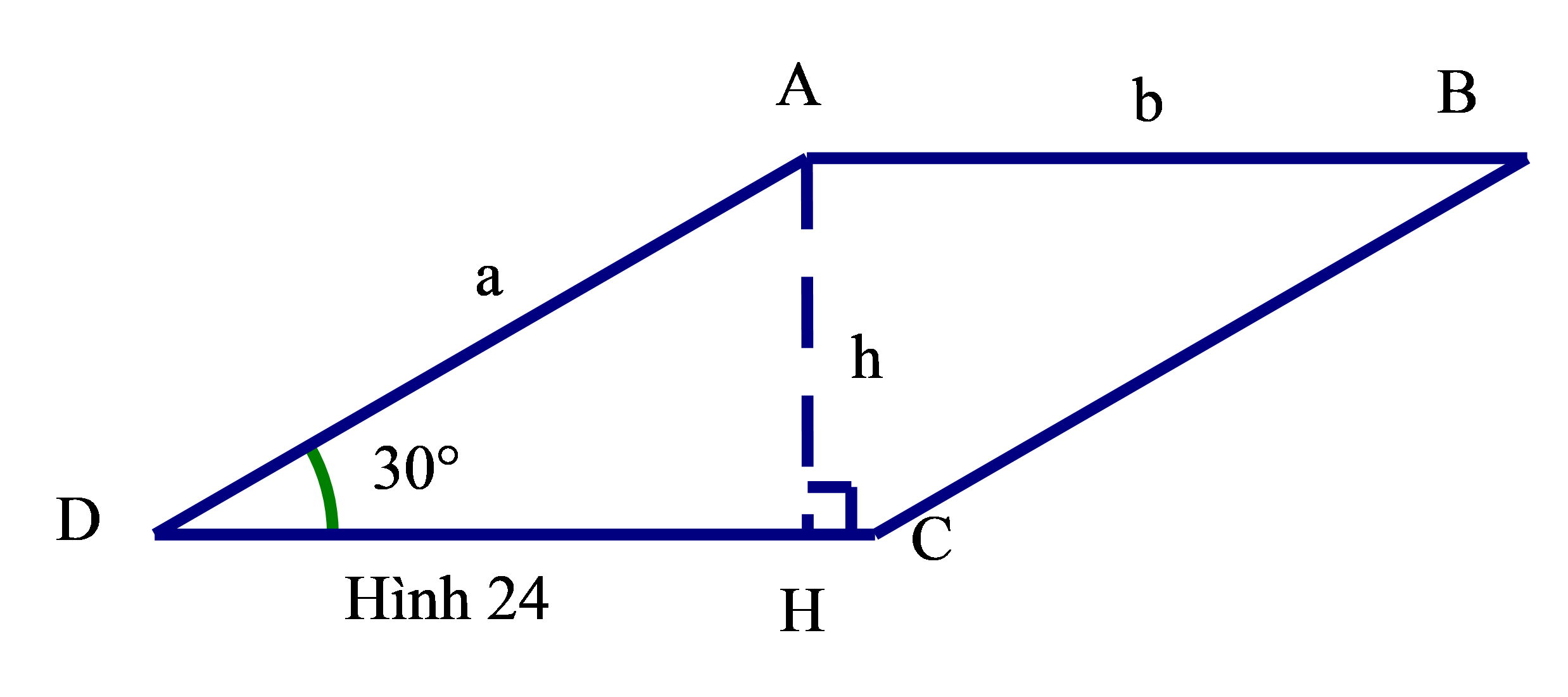
Bài 6: Tính diện tích hình bình hành ABCD có $AD=a,$$AB=b,$$\hat{D}={30}^o$(hình 24)

Bài 7: Cho tam giác ABC vuông tại A (AB<AC). GỌi I là trung điểm của cạnh BC. Qua I vẽ IM vuông góc với AB tại M và IN vuông góc với AC tại N. Gọi D là điểm đối xứng của I qua N.

a) Tứ giác ADCI là hình gì?

b) Đường thẳng BN cắt DC tại K. Chứng minh rằng $\frac{DK}{DC}=\frac{1}{3}$

c) Cho AB=12cm, BC=20cm. tính diện tích hình ADCI.

Bài 8: Cho ABCD là hình thang cân(AB//CD), E, N, G, M lần lượt là trung điểm của AB, BC, CD, DA.

a) Tứ giác MENG là hình gì?

b) Cho $S_{ABCD}=800m^2$. Tính $S_{MENG}$

Bài 9: Cho hình thoi ABCD có AC=10cm, BD=6cm. Gọi E, F, G, H theo thứ tự là trung điểm của AB, BC, CD, DA.

a) Tứ giác EFGH là hình gì? Vì sao?

b) Tính diện tích hình thoi ABCD

c) Tính diện tích tứ giác EFGH.

Bài 10: Để tính diện tích hình thang cân, người Ai Cập có lấy nửa tổng hai đáy nhân với cạnh bên. Nếu một hình thang cân có các cạnh đáy bằng 4m và 6m, cạnh bên bằng 20m thì sai số trong cách tính trên so với cách tính đúng là bao nhiêu phần trăm.