Một chiếc cổng parabol dạng \(y = \dfrac{{ - 1}}{2}{x^2}\) có chiều rộng \(d = 8m.\) Hãy tính chiều cao \(h\) của cổng ?
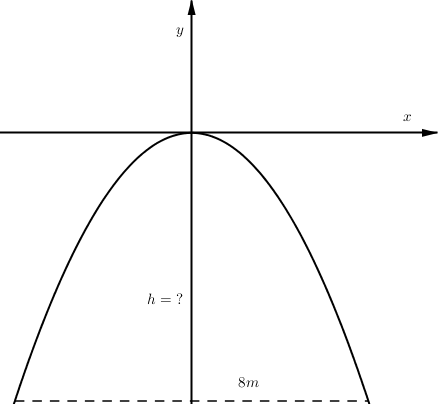
Khoảng cách từ chân cổng đến trục đối xứng \(Oy\) là \(\dfrac{8}{2} = 4\). Hoành độ 2 chân cổng là \( - 4\) và \(4\).
Tung độ chân cổng là \(y = \dfrac{{ - 1}}{2}{.4^2} = - 8\)
Chiều cao của cổng là \(\left| { - 8} \right| = 8m\)
Một cái cổng hình parabol có dạng \(y = - \dfrac{1}{2}{x^2}\) có chiều rộng \(d = 4m.\)
Tính chiều cao \(h\) của cổng (xem hình minh họa)
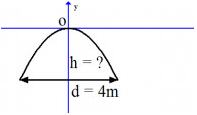
Đáp án: \(h = \)
$m$
Đáp án: \(h = \)
$m$
Bước 1:
Gọi hai điểm chân cổng là \(A\left( {{x_A};{y_A}} \right)\) và \(B\left( {{x_B};{y_B}} \right)\) thì ta có \({y_A} = {y_B}\) và \(\left| {{x_A}} \right| = \left| {{x_B}} \right|.\)
Vì \(d = 4\) nên \(\left| {{x_A}} \right| = \left| {{x_B}} \right| = 2.\)
Bước 2: Tính $h$
Vậy \(h = \left| {{y_A}} \right| = \left| { - \dfrac{1}{2}x_A^2} \right| = \left| { - \dfrac{1}{2}{{.2}^2}} \right| = 2\,\left( m \right).\)
Đạn bắn ra từ 1 máy bắn đá có quỹ đạo là một parabol \((P)\). Biết rằng đạn của máy bắn đá bắn xa \(100\;{\rm{m}}\) và tại thời điểm đạn cao \(60\;{\rm{m}}\) thì đạn bị bắn xa \(80\;{\rm{m}}\) theo chiều song song với mặt đất.
Vị trí đạn bay cao nhất cách mặt đất bao nhiêu?
Bước 1: Đặt hệ trục tọa độ. Gọi \((P):y = a{x^2} + bx + c\). Tìm (P).
Đặt hệ trục như hình vẽ.
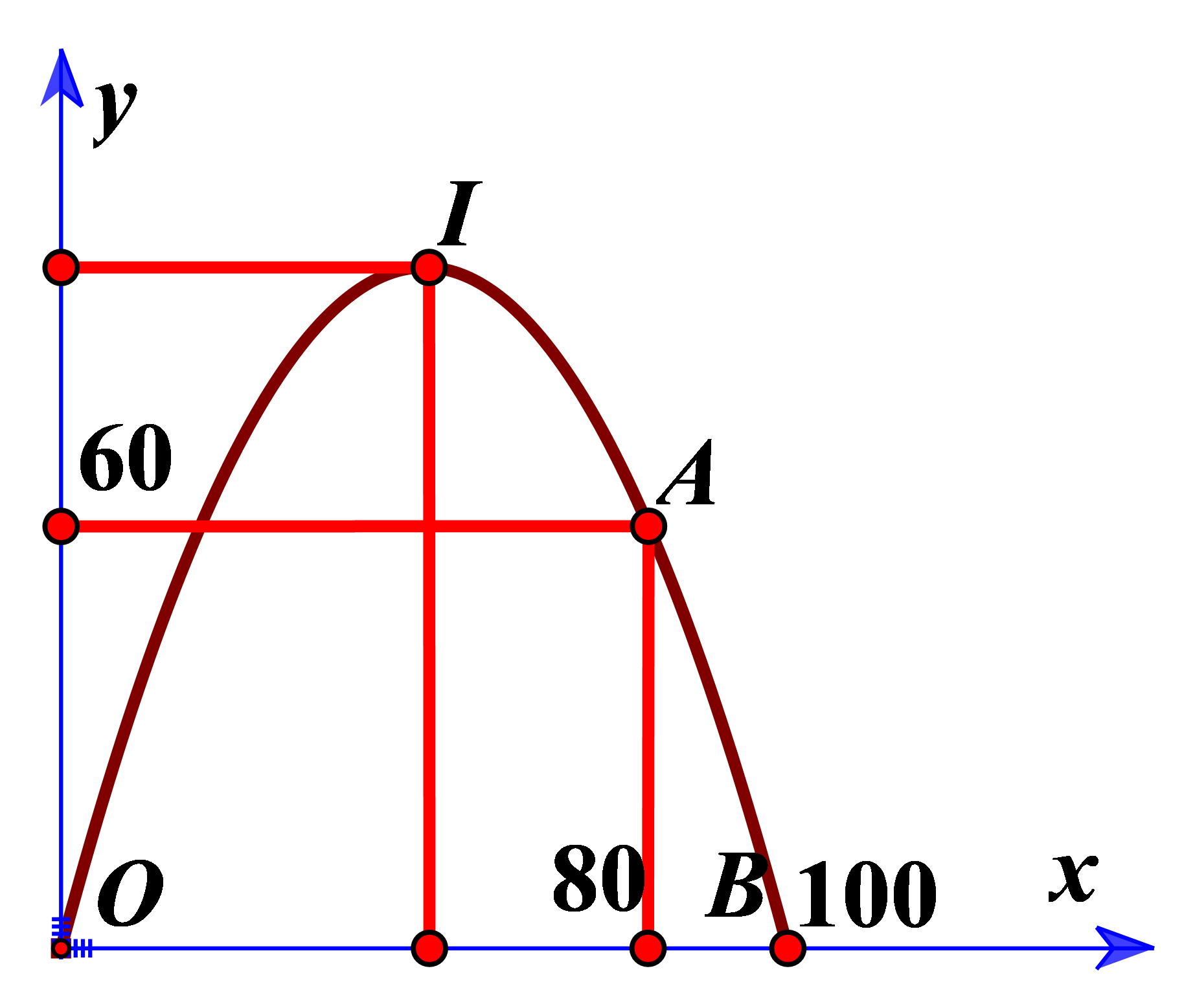
Gọi \((P):y = a{x^2} + bx + c\).
Ta có \((P)\) qua \(O(0;0),A(80;60)\) và \(B(100;0)\)
\( \Rightarrow \left\{ {\begin{array}{*{20}{l}}{c = 0}\\{{{80}^2}a + 80b = 60}\\{{{100}^2}a + 100b = 0}\end{array} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{a = - \dfrac{3}{{80}}}\\{b = \dfrac{{15}}{4}}\end{array}} \right.} \right.\)
\( \Rightarrow (P):y = - \dfrac{3}{{80}}{x^2} + \dfrac{{15}}{4}x\)
Bước 2: Tìm đỉnh của (P)
Vị trí đạn bay cao nhất cách mặt đất là \({y_I} = - \dfrac{\Delta }{{4a}} = - \dfrac{{{b^2} - 4ac}}{{4a}} = \dfrac{{375}}{4} = 93,75m\).
Đạn bắn ra từ 1 máy bắn đá có quỹ đạo là một parabol \((P)\). Biết rằng đạn của máy bắn đá bắn xa \(100\;{\rm{m}}\) và tại thời điểm đạn cao \(60\;{\rm{m}}\) thì đạn bị bắn xa \(80\;{\rm{m}}\) theo chiều song song với mặt đất.

Máy bắn đá cách tường thành địch \(90\;{\rm{m}}\). Biết tường thành cao \(30\;{\rm{m}}\). Hỏi chiều cao khi đạn bay đến tường thành thì cao hơn hay thấp hơn tường thành bao nhiêu mét?
\((P):y = - \dfrac{3}{{80}}{x^2} + \dfrac{{15}}{4}x\).
Vì máy bắn đá cách tường thành địch 90 m nên \(x = 90 \Rightarrow y = 33,75(m) > 30(m)\)
\( \Rightarrow \) đạn pháo cao hơn tường thành 3,75m
Đạn bắn ra từ 1 máy bắn đá có quỹ đạo là một parabol \((P)\). Biết rằng đạn của máy bắn đá bắn xa \(100\;{\rm{m}}\) và tại thời điểm đạn cao \(60\;{\rm{m}}\) thì đạn bị bắn xa \(80\;{\rm{m}}\) theo chiều song song với mặt đất.

Địch xây chòi phòng thủ cao \(20\;{\rm{m}}\) phía trước tường thành. Hỏi phải đặt máy bắn đá cách chòi bao xa để đạn có thể bắn trúng chòi? Biết rằng để tránh bị địch tấn công thì máy bắn đá phải đặt cách thành địch ít nhất \(50\;{\rm{m}}\).
Để máy bắn đá có thể bắn trúng chòi cao \(20\;{\rm{m}}\) thì
\( - \dfrac{3}{{80}}{x^2} + \dfrac{{15}}{4}x = 20 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 94,35(m)}\\{x = 5,65(m)(L)}\end{array}} \right.\)
Vậy cần đặt máy bắn đá cách chòi 94,35 m để đạn có thể bắn trúng chòi.

