Chúng tôi giới thiệu Giải sách bài tập Toán lớp 12 Bài 1: Sự đồng biến, nghịch biến của hàm số chi tiết giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 12. Mời các bạn đón xem:
Giải SBT Toán 12 Bài 1: Sự đồng biến, nghịch biến của hàm số
a)
b)
c)
d)
Phương pháp giải:
- Tính .
- Tìm nghiệm của phương trình .
- Xét dấu và kết luận.
Lời giải:
a)
TXĐ: R
Xét dấu :
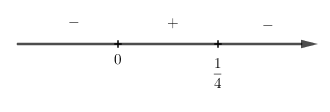
Ta thấy, nên hàm số đồng biến trên khoảng .
nên hàm số nghịch biến trên các khoảng và .
b)
TXĐ: R
Bảng biến thiên:
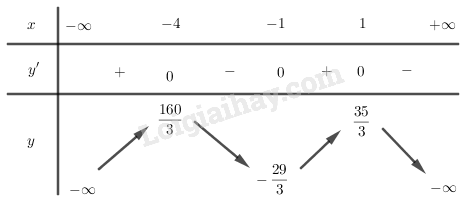
Vậy hàm số đã cho đồng biến trên các khoảng và , nghịch biến trên các khoảng và .
c)
TXĐ: R
y'=0 <=>
nên hàm số đồng biến trên các khoảng và .
nên hàm số nghịch biến trên khoảng .
d)
TXĐ: R
nên hàm số đồng biến trên khoảng .
nên hàm số nghịch biến trên khoảng .
a)
b)
c)
d)
e)
g)
Phương pháp giải:
a) - Tìm TXĐ.
- Tính theo công thức
- Xét dấu và kết luận khoảng đồng biến, nghịch biến.
b) - Tìm TXĐ.
- Tính theo công thức
- Xét dấu và kết luận khoảng đồng biến, nghịch biến.
c) - Tìm TXĐ.
- Tính theo công thức
- Xét dấu và kết luận khoảng đồng biến, nghịch biến.
d) - Tìm TXĐ.
- Tính theo công thức .
- Xét dấu và kết luận khoảng đồng biến, nghịch biến.
e) - Tìm TXĐ.
- Tính theo công thức .
- Xét dấu và kết luận khoảng đồng biến, nghịch biến.
Lời giải:
a)
TXĐ:
Vậy hàm số nghịch biến trên các khoảng và .
b)
TXĐ:
Ta có:
nên hàm số đồng biến trên khoảng .
nên hàm số nghịch biến trên khoảng .
c)
TXĐ:
Vậy hàm số nghịch biến trên các khoảng .
d)
TXĐ: .
Ta có:
.
Bảng biến thiên:
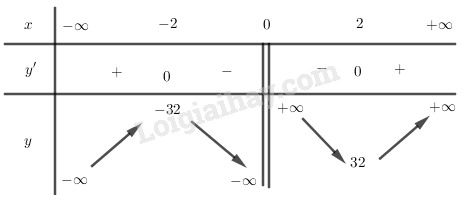
Vậy hàm số đồng biến trên các khoảng và .
Hàm số nghịch biến trên các khoảng và .
e)
TXĐ:
Ta có:
Khi đó
Bảng biến thiên:
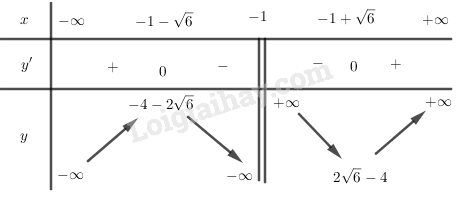
Vậy hàm số đã cho đồng biến trên các khoảng
và nghịch biến trên các khoảng
g)
TXĐ:
Ta có: .
Vậy hàm số đồng biến trên các khoảng và .
a)
b)
Phương pháp giải:
- Tìm tập xác định.
- Tính và tìm nghiệm của .
- Xét dấu của và kết luận khoảng đồng biến, nghịch biến của hàm số.
Lời giải:
a)
Ta có:
.
Bảng biến thiên:
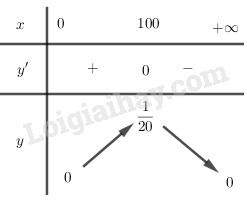
Vậy hàm số đồng biến trên khoảng và nghịch biến trên khoảng
b)
TXĐ:
;
Bảng biến thiên:
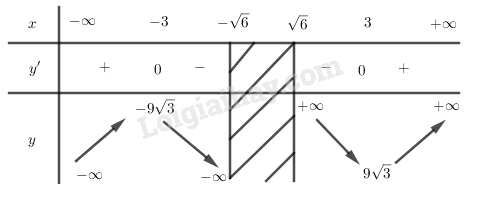
Vậy hàm số đồng biến trên các khoảng , nghịch biến trên các khoảng .
a)
b) ,
Phương pháp giải:
- Tìm TXĐ.
- Tính và xét dấu .
- Kết luận.
Lời giải:
a)
.
với mọi
Dấu “=” xảy ra chỉ tại và .
Vậy hàm số đồng biến trên đoạn .
b) ,
Xét hàm số với .
Với ta có:
⟺ < 0
⟺ ,k = 0, 1, 2 ….
⟺ , k = 0, 1, 2 ……..
Do đó, hàm số đồng biến trên các khoảng
và nghịch biến trên các khoảng
……,
với k = 0, 1, 2 …
Bài 1.5 trang 8 SBT Giải tích 12: Xác định để hàm số sau:
a) đồng biến trên từng khoảng xác định;
b) nghịch biến trên
Phương pháp giải:
a) - Tìm TXĐ .
- Hàm số phân thức bậc nhất trên bậc nhất đồng biến trên nếu .
b) - Hàm số đa thức bậc ba nghịch biến trên nếu .
- Tam thức bậc hai
Lời giải:
a) đồng biến trên từng khoảng xác định;
Tập xác định: D = R\{m}
Hàm số đồng biến trên từng khoảng xác định
b) nghịch biến trên
Tập xác định:
Hàm số nghịch biến trên R
Bài 1.6 trang 8 SBT Giải tích 12: Chứng minh phương trình sau có nghiệm duy nhất
Sử dụng phương pháp hàm số:
- Xét hàm số vế trái và chứng minh nó đơn điệu trên .
- Từ đó suy ra phương trình có nghiệm duy nhất.
Lời giải:
Đặt
Hàm số xác định, liên tục và có đạo hàm tại mọi x ∈ R
Ta có: và .
Hàm số đồng biến trên R và có một nghiệm
Vậy phương trình đã cho có một nghiệm duy nhất.
a) ,
b) với
Phương pháp giải:
a) Xét hàm và chứng minh nó đồng biến trên .
Từ đó suy ra điều phải chứng minh.
b) Xét các hàm số và trên và chứng minh chúng nghịch biến trên .
Từ đó suy ra điều phải chứng minh.
Lời giải:
a) ,
Xét hàm trên khoảng ta có:
với vì với mọi nên
Do đó hàm số đồng biến trên
với mọi .
b) với
Xét trên ta có: .
Vì nên nên hàm số nghịch biến trên
Do đó
Xét trên ta có:
Vì nên hay nghịch biến trên
Do đó hay
Từ và ta được với . (đpcm)
Phương pháp giải:
Hàm số nghịch biến trên với mọi nếu f ′ ( x ) ≤ 0 , ∀ x ∈ D .
Lời giải:
nghịch biến trên R nếu ta có:
.
Vì nên
Bài 1.9 trang 8 SBT Giải tích 12: Khẳng định nào sau đây là đúng?
A. là hàm số chẵn.
B. Hàm số xác định trên .
C. Hàm số đồng biến trên .
D. Hàm số nghịch biến trên .
Phương pháp giải:
Xét tính đúng sai của mỗi đáp án, sử dụng tính chẵn lẻ, tính đơn điệu của hàm số.
Lời giải:
Đáp án A: TXĐ: .
Có nên hàm số lẻ trên .
A sai.
Đáp án B: ĐKXĐ: nên TXĐ: .
B sai.
Đáp án C: TXĐ:
Có nên hàm số đồng biến trên .
C đúng.
Chọn C.
Chú ý:
Ngoài ra các em cũng có thể kiểm tra thêm đáp án D: nên hàm số đồng biến trên . Do đó D sai.
Bài 1.10 trang 8 SBT Giải tích 12: Hàm số nghịch biến trên khoảng:
A.
B.
C.
D.
Phương pháp giải:
- Tìm TXĐ .
- Tính và tìm nghiệm của trên .
- Xét dấu và suy ra khoảng đồng biến, nghịch biến của hàm số.
Lời giải:
TXĐ: .
Ta có: .
Bảng biến thiên:
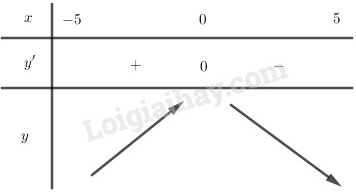
Hàm số đã cho nghịch biến trên .
Chọn C.
Bài 1.11 trang 8 SBT Giải tích 12: Hàm số đồng biến trên khoảng
A.
B.
C.
D.
Phương pháp giải:
- Tìm TXĐ .
- Tính và tìm nghiệm của trên .
- Xét dấu và suy ra khoảng đồng biến, nghịch biến của hàm số.
Lời giải chi tiết:
TXĐ: .
Có
Do đó hàm số đồng biến trên .
Chọn B.
Bài 1.12 trang 8 SBT Giải tích 12: Phương trình nào sau đây có nghiệm duy nhất trên ?
A.
B.
C.
D.
Phương pháp giải:
Xét tính đơn điệu của mỗi hàm số vế trái, hàm số nào đơn điệu trên thì phương trình có nghiệm duy nhất.
Lời giải:
Đáp án C vì: Xét hàm có .
và nên hàm số đồng biến trên .
Mặt khác nên .
Hàm số liên tục trên nên tồn tại để hay phương trình có nghiệm duy nhất trên .
Chọn C.
Chú ý:
Cách khác:
+) Phương trình (vô nghiệm vì ) nên loại A.
+) Các phương trình và có nhiều hơn một nghiệm nên loại B, D.
Chọn C.
Bài 1.13 trang 8 SBT Giải tích 12: Phương trình nào sau đây có nghiệm duy nhất trên ?
A.
B.
C.
D.
Phương pháp giải:
Xét tính đơn điệu của mỗi hàm số vế trái, hàm số nào đơn điệu trên thì phương trình có nghiệm duy nhất.
Lời giải chi tiết:
Đáp án B vì: Xét hàm có nên hàm số đồng biến trên .
Mặt khác, nên phương trình có nghiệm duy nhất trên .
Chọn B.
Bài 1.14 trang 8 SBT Giải tích 12: Phương trình nào sau đây có nghiệm duy nhất trên ?
A.
B.
C.
D.
Phương pháp giải:
Loại đáp án, xét các đáp án bằng cách giải mỗi phương trình và suy ra số nghiệm.
Lời giải chi tiết:
Đáp án A: nên phương trình có nghiệm.
Đáp án B: Xét hàm có và nên hay hàm số nghịch biến trên .
Mà nên , hàm số liên tục trên nên phương trình có nghiệm .
Kết hợp với hàm số nghịch biến trên nên phương trình đã cho có nghiệm duy nhất trên .
Chọn B.
Bài 1.15 trang 8 SBT Giải tích 12: Tìm giá trị của tham số để hàm số đồng biến trên .
A.
B.
C.
D.
Phương pháp giải:
- Tính .
- Hàm số đồng biến trên .
Lời giải chi tiết:
TXĐ: .
Ta có: .
Hàm số đồng biến trên
.
Chọn D.
Bài 1.16 trang 8 SBT Giải tích 12: Tìm giá trị của tham số để hàm số nghịch biến trên từng khoảng xác định.
A. hoặc
B.
C.
D.
Phương pháp giải:
- Tính .
- Hàm số nghịch biến trên từng khoảng xác định nếu trên từng khoảng xác định.
Lời giải chi tiết:
TXĐ: .
Ta có: .
Hàm số nghịch biến trên từng khoảng và nếu .
Chọn A.

