Giải Toán 12 Bài 4: Phương trình bậc hai với hệ số thực

76 lượt xem

Bài trước

Bài sau

Chúng tôi giới thiệu Giải bài tập Toán lớp 12 Bài 4: Phương trình bậc hai với hệ số thực chính xác, chi tiết nhất giúp học sinh dễ dàng làm bài tập Phương trình bậc hai với hệ số thực lớp 12.

Giải bài tập Toán lớp 12 Bài 4: Phương trình bậc hai với hệ số thực

Trả lời câu hỏi giữa bài

Trả lời câu hỏi 1 trang 139 SGK Giải tích 12: Thế nào là căn bậc hai của số thực dương

a

Lời giải:

Căn bậc hai của một số thực dương $a$ là một số thực $b$ sao cho $b^{2} = a$

Câu hỏi và bài tập (trang 140 SGK Giải tích 12)

Bài 1 trang 140 SGK Giải tích 12: Tìm các căn bậc hai phức của các số sau:

- 7; - 8; - 12; - 20; - 121

Phương pháp giải:

Ta viết $- a = (- 1) . a = i^{2} . a = {(\pm i . \sqrt{a})}^{2} (a > 0)$

Lời giải:

Căn bậc hai của $- 7$ là $\pm i \sqrt{7}$ ;

Căn bậc hai của $- 8$ là $\pm 2 \sqrt{2} i$ ;

Căn bậc hai của $- 12$ là $\pm 2 \sqrt{3} i$ ;

Căn bậc hai của $- 20$ là $\pm 2 \sqrt{5} i$ ;

Căn bậc hai của $- 121$ là $\pm 11 i$

Bài 2 trang 140 SGK Giải tích 12: Giải các phương trình sau trên tập hợp số phức:

a) $- 3 z^{2} + 2 z - 1 = 0$ ;

b) $7 z^{2} + 3 z + 2 = 0$ ;

c) $5 z^{2} - 7 z + 11 = 0$

Phương pháp giải:

Phương trình bậc hai: $a z^{2} + b z + c = 0$ $(a \neq 0)$

Bước 1: Tính: $Δ = b^{2} - 4 a c$ (hoặc $Δ^{'} = b^{' 2} - a c$ ).

Bước 2:

Nếu $Δ = 0$ , phương trình có nghiệm kép $x = - \frac{b}{2 a}$ .

Nếu $Δ > 0$ , phương trình có hai nghiệm thực phân biệt $x = \frac{- b \pm \sqrt{Δ}}{2 a} .$

Nếu $Δ < 0$ , gọi $δ$ là một căn bậc hai của $Δ$ .

Phương trình có hai nghiệm phức $x_{1, 2} = \frac{- b \pm δ}{2 a}$

(Với $δ = \pm i . \sqrt{- Δ}$ )

Lời giải:

Ta có $∆^{'} = 1^{2} - (- 3) . (- 1) = 1 - 3 = - 2 < 0.$

Ta viết: $∆^{'} = - 2 = 2. i^{2}$ (Vì $i^{2} = - 1$ ).

$\Rightarrow δ = \sqrt{Δ^{'}} = \sqrt{2 i^{2}} = \pm i \sqrt{2}$

Vậy nghiệm của phương trình là $z = \frac{1 \pm i \sqrt{2}}{3}$

Ta có $∆ = 3^{2} - 4.7.2 = 9 - 56 = - 47$ .

Ta viết: $∆ = - 47 = 47. i^{2}$ (Vì $i^{2} = - 1$ ).

$\Rightarrow δ = \sqrt{Δ} = \sqrt{47 i^{2}} = \pm i \sqrt{4} 7$

Vậy nghiệm của phương trình là $z = \frac{- 3 \pm i \sqrt{47}}{14}$ ;

Ta có $∆ = 49 - 4.5.11 = - 171$ .

Ta viết: $∆ = - 171 = 171. i^{2}$ (Vì $i^{2} = - 1$ ).

$\Rightarrow δ = \sqrt{Δ} = \sqrt{171. i^{2}} = \pm i \sqrt{1} 71$

Vậy nghiệm của phương trình là $z = \frac{7 \pm i \sqrt{171}}{10}$

Bài 3 trang 140 SGK Giải tích 12: Giải các phương trình sau trên tập hợp số phức:

a) $z^{4} + z^{2} - 6 = 0$ ;

b) $z^{4} + 7 z^{2} + 10 = 0$

Phương pháp giải:

Phương pháp giải phương trình $a z^{4} + b z^{2} + c = 0 (a \neq 0)$ .

Bước 1: Đặt $z^{2} = t$ , đưa về phương trình bậc hai ẩn t.

Bước 2: Giải phương trình bậc hai ẩn t: $a t^{2} + b t + c = 0$ .

Bước 3: Từ nghiệm t, ta giải tìm nghiệm x bằng cách tìm căn bậc hai của t.

Lời giải:

Đặt $t = z^{2}$ , ta được phương trình $t^{2} + t - 6 = 0 \Leftrightarrow [\begin{array}{l} t = 2 \\ t = - 3 \end{array}$

Khi $t = 2 \Rightarrow z^{2} = 2 \Rightarrow z_{1, 2} = \pm \sqrt{2}$

Khi $t = - 3 \Rightarrow z^{2} = - 3 \Rightarrow z_{3, 4} = \pm i \sqrt{3}$

Vậy phương trình có bốn nghiệm là: $\pm \sqrt{2}$ và $\pm i \sqrt{3}$ .

Đặt $t = z^{2}$ , ta được phương trình $t^{2} + 7 t + 10 = 0 \Leftrightarrow [\begin{array}{l} t = - 2 \\ t = - 5 \end{array}$

Khi $t = - 2 \Rightarrow z^{2} = - 2 \Rightarrow z_{1, 2} = \pm i \sqrt{2}$

Khi $t = - 5 \Rightarrow z^{2} = - 5 \Rightarrow z_{3, 4} = \pm i \sqrt{5}$

Vậy phương trình có bốn nghiệm là: $\pm i \sqrt{2}$ và $\pm i \sqrt{5}$ .

Bài 4 trang 140 SGK Giải tích 12: Cho

a, b, c \in R

a \neq 0

z_{1}

và

z_{2}

là hai nghiệm của phương trình

a z^{2} + b z + c = 0

Hãy tính $z_{1} + z_{2}$ và $z_{1} z_{2}$ theo các hệ số $a, b, c$ .

Phương pháp giải:

+) Tính biệt thức $Δ = b^{2} - 4 a c$ .

+) Chia các trường hợp của $Δ$ :

TH1: $Δ \geq 0$ , sử dụng kết quả của định lí Vi-et đã biết.

TH2: $Δ < 0$ , gọi $δ$ là một căn bậc hai của $Δ$ , suy ra các nghiệm phức của phương trình bậc hai và tính tổng, tích các nghiệm phức đó.

Lời giải:

Yêu cầu của bài toán này là kiểm chứng định lí Vi-ét đối với phương trình bậc hai trên tập số phức.

+) Trường hợp $∆ \geq 0$ , theo định lí vi-ét ta có: ${\begin{cases} z_{1} + z_{2} = - \frac{b}{a} \\ z_{1} z_{2} = \frac{c}{a} \end{cases}$

+) Trường hợp $∆ < 0$ , gọi $δ$ là một căn bậc hai của $Δ$ , khi đó các nghiệm của phương trình là:

$\begin{array}{l} z_{1} = \frac{- b + δ}{2 a}; z_{2} = \frac{- b - δ}{2 a} \\ \Rightarrow z_{1} + z_{2} = \frac{- b + δ - b - δ}{2 a} = \frac{- b}{a} \\ z_{1} z_{2} = \frac{(- b + δ) (- b - δ)}{4 a^{2}} = \frac{b^{2} - δ^{2}}{4 a^{2}} \\ = \frac{b^{2} - (b^{2} - 4 a c)}{4 a^{2}} = \frac{4 a c}{4 a^{2}} = \frac{c}{a} \end{array}$

Vậy kết quả của định lí Vi-et vẫn đúng trong trường hợp $∆ < 0$ .

Bài 5 trang 140 SGK Giải tích 12: Cho

z = a + b i

là một số phức. Hãy tìm một phương trình bậc hai với hệ số thực nhận

z

và

\bar{z}

làm nghiệm

Phương pháp giải:

Cách 1:

$z, \bar{z}$ là nghiệm của phương trình $(x - z) (x - \bar{z}) = 0$ .

Thay $z, \bar{z}$ và phương trình trên, đưa về đúng dạng phương trình bậc hai.

Cách 2:

Tính $S = z + \bar{z}, P = z . \bar{z}$ , khi đó $z, \bar{z}$ là nghiệm của phương trình $x^{2} - S x + P = 0$

Lời giải:

Cách 1:

Một phương trình bậc hai nhận $z$ và $\bar{z}$ làm nghiệm là

$\begin{array}{l} (x - z) (x - \bar{z}) = 0 \\ \Leftrightarrow x^{2} - x . \bar{z} - x . z + z . \bar{z} = 0 \\ \Leftrightarrow x^{2} - (z + \bar{z}) x + z . \bar{z} = 0 \\ \Leftrightarrow x^{2} - (a + b i + a - b i) + (a + b i) (a - b i) = 0 \\ \Leftrightarrow x^{2} - 2 a x + a^{2} + b^{2} = 0 \end{array}$

Vậy một phương trình bậc hai cần tìm là $x^{2} - 2 a x + a^{2} + b^{2} = 0$

Cách 2:

Ta có:

$\begin{array}{l} z + \bar{z} = a + b i + a - b i = 2 a \\ z . \bar{z} = (a + b i) (a - b i) = a^{2} + b^{2} \end{array}$

$\Rightarrow z, \bar{z}$ là nghiệm của phương trình $x^{2} - 2 a x + a^{2} + b^{2} = 0$ .

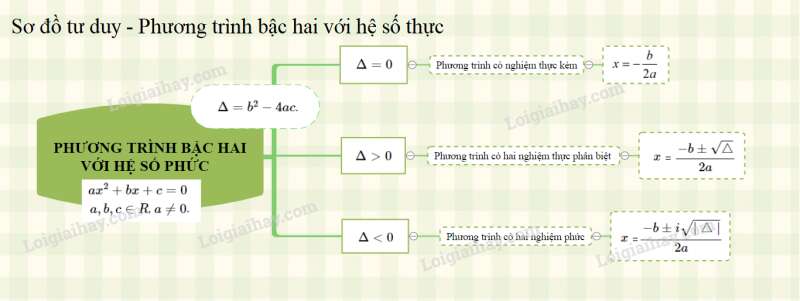
Lý thuyết Bài 4: Phương trình bậc hai với hệ số thực

Kiến thức cơ bản

- Các căn bậc hai của số thực $a < 0$ là $\pm i \sqrt{| a |}$

- Xét phương trình bậc hai $a x^{2} + b x + c = 0$ với $a, b, c \in R$ , $a \neq 0$ .

Đặt $Δ = b^{2} - 4 a c$ .

- Nếu $∆ = 0$ thì phương trình có một nghiệm kép (thực) $x = - \frac{b}{2 a}$ .

- Nếu $∆ > 0$ thì phương trình có hai nghiệm thực $x_{1, 2}$ = $\frac{- b \pm \sqrt{△}}{2 a}$

- Nếu $∆ < 0$ thì phương trình có hai nghiệm phức $x_{1, 2}$ = $\frac{- b \pm i \sqrt{| △ |}}{2 a}$

Nhận xét. Trên $C$ , mọi phương trình bậc hai đều có hai nghiệm (không nhất thiết phân biệt). Tổng quát, mọi phương trình bậc $n$ , $n \in N^{*}$ đều có $n$ nghiệm phức (các nghiệm không nhất thiết phải phân biệt).

Sơ đồ tư duy về phương trình bậc hai với hệ số thực

Xem thêm các chương trình khác:

Bài trước

Bài sau

Giải SGK, SBT, Chuyên đề Toán Học Lớp 12

Giải Toán 12 Bài 4: Phương trình bậc hai với hệ số thực

Xem thêm các chương trình khác: