Chúng tôi giới thiệu Giải bài tập Toán lớp 12 Ôn tập chương I - Khối đa diện chính xác, chi tiết nhất giúp học sinh dễ dàng làm bài tập Ôn tập chương I - Khối đa diện lớp 12.
Giải bài tập Toán lớp 12 Ôn tập chương I - Khối đa diện
Câu hỏi và bài tập (trang 26, 27 SGK Hình học 12)
Phương pháp giải:
Suy ra điều kiện về các đỉnh, cạnh, mặt của một đa diện từ khái niệm của khối đa diện.
Lời giải:
Các đỉnh, cạnh, mặt của một đa diện phải thỏa mãn những tính chất:
- Mỗi đỉnh là đỉnh chung của ít nhất ba cạnh, ba mặt;
- Mỗi cạnh là cạnh chung của đúng hai mặt;
- Hai mặt bất kì hoặc không có điểm chung, hoặc có một đỉnh chung, hoặc có đúng một cạnh chung.
Phương pháp giải:
Dựa vào tính chất các đường của khối đa diện:
- Mỗi cạnh của đa giác nào cũng là cạnh chung của đúng hai đa giác.
Dễ thấy cạnh không thỏa mãn tính chất này nên hình không là khối đa diện.
Lời giải:
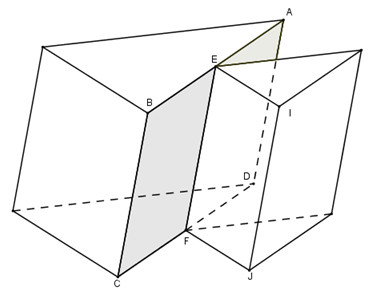
Ví dụ, hình sau được tạo bởi các đa giác nhưng không phải là một đa diện.
Vì là giao của hai đa giác và nhưng nó không phải là cạnh chung của hai đa giác đó.
Bài 3 trang 26 SGK Hình học 12: Thế nào là một khối đa diện lồi? Tìm ví dụ trong thực tế mô tả một khối đa diện lồi, một khối đa diện không lồi.Phương pháp giải:
Khối đa diện không thỏa mãn điều kiện trên thì là khối đa diện không lồi.
Lời giải:
Khối đa diện được gọi là khối đa diện lồi nếu đoạn thẳng nối hai điểm bất kỳ của luôn thuộc .
Khối đa diện lồi:
Chẳng hạn: Hình hộp chữ nhật (viên gạch đặc, bao diêm, các thùng đựng)

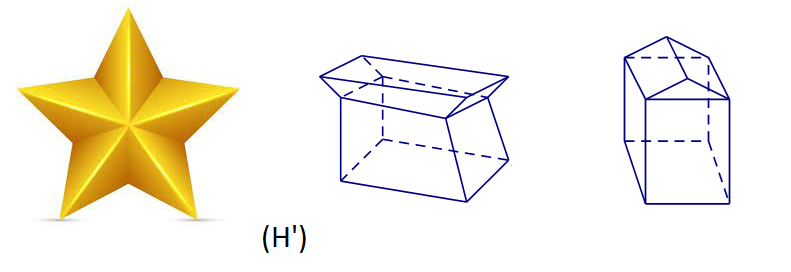
Các hình mô tả một khối da diện lồi, hình mô tả một khối đa diện không lồi.
Phương pháp giải:
Thể tích khối lăng trụ: , trong đó là diện tích đáy, là chiều cao khối lăng trụ.
Thể tích khối chóp: , trong đó là diện tích đáy, là chiều cao khối lăng trụ.
Lời giải:
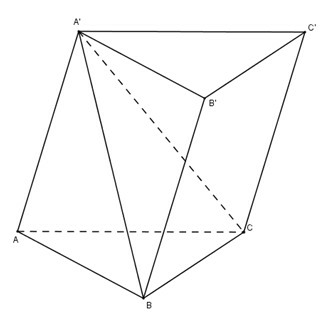
Gọi là diện tích đáy và là chiều cao của khối lăng trụ ta có:
lăng trụ =
Gọi là diện tích đáy và là chiều cao của khối chóp ta có:
( cùng bằng diện tích tam giác
( cùng bằng khoảng cách từ đến mp )
chóp = (Vì diện tích đáy và chiều cao bằng nhau)
Vậy tỉ lệ thể tích giữa hình lăng trụ và hình chóp là:
Phương pháp giải:
+) Gọi là trọng tâm của , chứng minh .
+) Sử dụng các hệ thức lượng trong tam giác vuông tính .
Lời giải:
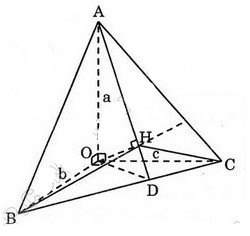
Kẻ ta chứng minh chính là đường cao của hình chóp.
Vậy chính là đường cao của hình chóp.
.
Tam giác vuông tại nên
Áp dụng hệ thức lượng trong tam giác vuông ta có:
nên .
Áp dụng định lí Pitago trong tam giác vuông ta có:
.
Áp dụng hệ thức lượng trong tam giác vuông ta có: nên
.
Cách khác:
Tam giác vuông tại có là đường cao nên
Tam giác vuông tại có chiều cao nên
Chú ý: Ta thấy khi là tứ diện vuông ( đôi một vuông góc) thì: .
Từ nay về sau các em sử dụng kết quả này để các bài toán nhanh chóng hơn.
a) Tính tỉ số thể tích của hai khối chóp và .
b) Tính thể tích của khối chóp .
Phương pháp giải:
a) + Hình chóp có các cạnh bên tạo với đáy góc bằng nhau thì chân đường cao trùng với tâm đường tròn ngoại tiếp đáy.
Qua kẻ , chứng minh mặt phẳng qua và vuông góc với là .
+ Sử dụng công thức tỉ số thể tích: .
b) Tính thể tích khối chóp sau đó tính thể tích khối chóp .
Lời giải:
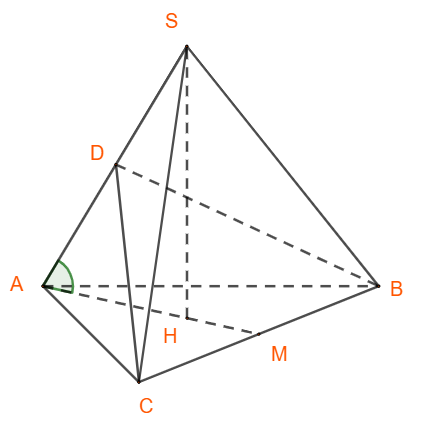
a) Vì hình chóp là hình chóp đều nên chân đường cao là tâm của đường tròn ngoại tiếp đáy.
Do đó là hình chiếu của lên nên góc giữa và bằng góc giữa và hay góc .
Gọi là trung điểm của cạnh thì là đường cao của tam giác đều :
=
Xét tam giác vuông ta có: .
Qua kẻ , khi đó ta có:
Khi đó mặt phẳng đi qua và vuông góc với
Xét tam giác vuông có:
Xét tam giác vuông có:
Áp dụng công thức tỉ số thể tích trong bài tập 4, 3 (trang 37 SGK) ta được:
b) Ta có: =
Từ kết quả câu a) ta có:
Phương pháp giải:
Hình chóp có các cạnh bên tạo với đáy các góc bằng nhau có hình chiếu của đỉnh trùng với tâm đường tròn nội tiếp đáy.
Áp dụng công thức tính thể tích trong đó là diện tích đáy và là chiều cao của khối chóp.
Lời giải:
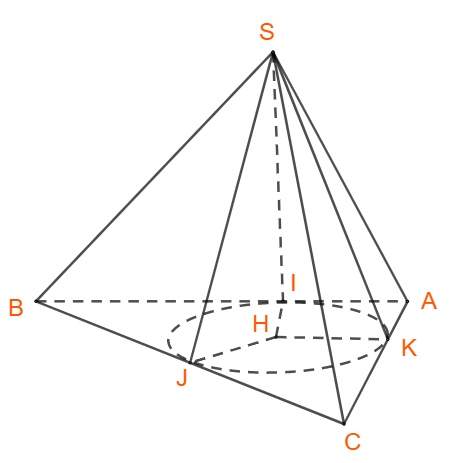
Kẻ và từ kẻ .
Từ định lý ba đường vuông góc, ta suy ra:
do đó:
+) Góc giữa hai mặt phẳng và là
+) Góc giữa hai mặt phẳng và là
+) Góc giữa hai mặt phẳng và là
Từ đây ta có: (c.g.v.g.n)
là tâm đường tròn nội tiếp .
Tam giác có chu vi:
Theo công thức Hê-rông, ta có:
Bán kính của đường tròn nội tiếp tam giác :
Xét tam giác vuông SHI có: =
Vậy thể tích khối chóp:
Phương pháp giải:
Chứng minh
Lời giải:
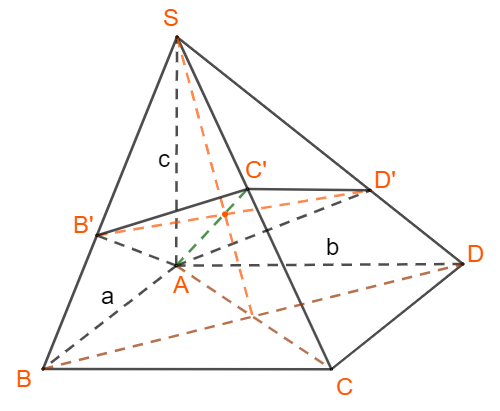
Ta có
Theo giả thiết (1)
Chứng minh tương tự ta có: (2)
Từ (1) và (2) suy ra hay
Do đó là đường cao của hình chóp .
Từ
Tương tự ta có:
Từ các kết quả trên, ta được:
(*)
Ta tính các yếu tố trên.
Tam giác vuông có là đường cao, nên ta có:
Tương tự, ta có:
Ta lại có:
Trong tam giác vuông là đường cao
đồng dạng (g.g)
Tương tự ta có:
Thay các kết quả này vào (*) ta được:
Phương pháp giải:
Hình chóp đều có chân đường cao trùng với tâm của đáy.
Xác định thiết diện của hình chóp cắt bởi mặt phẳng đi qua và song song với là tức giác
Chứng minh có hai đường chéo vuông góc
Chứng minh
Lời giải:
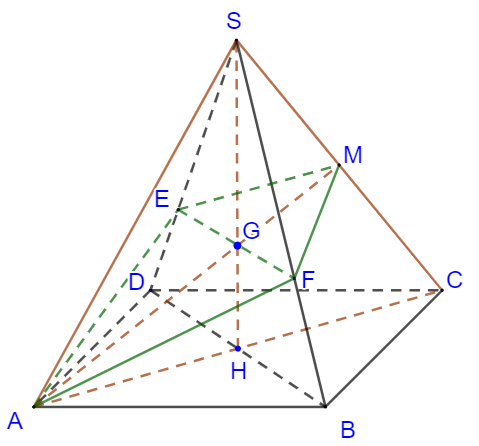
Gọi .
Hình chóp là hình chóp đều nên chân của đường cao chính là tâm của đáy.
Mặt phẳng đi qua và song song với cắt mặt phẳng theo một giao tuyến song song với \. Ta dựng giao tuyến như sau: Gọi là giao điểm của và . Qua ta dựng một đường thẳng song song với , đường này cắt ở và cắt ở .
Ta có: là hình chiếu vuông góc của trên
Tam giác cân có và góc nên nó là tam giác đều: là giao điểm của các trung tuyến và nên là trọng tâm của tam giác đều
Do
Vì
Tam giác là tam giác đều nên
Ta lại có
Tứ giác có hai đường chéo vuông góc với nhau nên có diện tích:
Mặt khác, tam giác là tam giác đều, là trung điểm của nên . Ta cũng có vì nên . Từ kết quả trên, suy ra .
Dễ thấy (do tam giác đều). Do đó: .
a) Tính thể tích khối tứ diện .
Phương pháp giải:
a) Gọi là trung điểm của . Chứng minh . Áp dụng công thức .
b) Mặt phẳng đi qua và trọng tâm tam giác , cắt và lần lượt tại và . Tính thể tích hình chóp .
Lời giải:
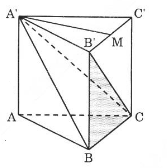
a) Ta tính thể tích hình chóp .
Gọi là trung điểm của , ta có: (1)
Lăng trụ là lăng trụ đứng nên:
(2)
Từ (1) và (2) suy ra hay là đường cao của hình chóp .
Ta có: =
Cách khác:
Ta chia khối lẳng trụ đã cho thành hình chóp và
Ta có: trong đó là diện tích đáy và là chiều cao của hình lăng trụ
Lại có:
Do đó,
Trong đó, tam giác là tam giác đều có độ dài cạnh bằng nên
Vì đây là hình lăng trụ đứng nên
Vậy thể tích hình chóp là:
b)
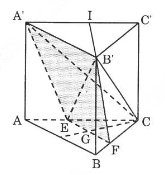
Thể tích hình chóp bằng tổng thể tích hai hình chóp:
- là thể tích hình chóp đỉnh , đáy là tam giác .
- là thể tích hình chóp đỉnh , đáy là tam giác .
Do nên dễ thấy . Ta cũng có: =
Hình chóp có chiều cao và diện tích đáy là:
Từ đây ta có:
Do nên
Gọi là trung điểm của ta có:
Hình chóp có chiều cao là bằng nên
Vậy thể tích hình chóp là: =
Phương pháp giải:
+) Xác định thiết diện của hình chóp khi cắt bởi mặt phẳng .
+) Phân chia và lắp ghép các khối đa diện.
Lời giải:
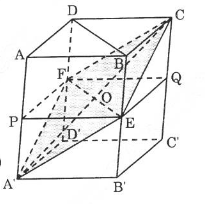
Ta xác định thiết diện của hình hộp khi cắt bởi . Mặt phẳng chứa đường thẳng mà là trung điểm của là trung điểm của .
Ta dễ dàng nhận xét rằng thiết diện chính là hình bình hành .
Mặt phẳng chia khối hộp thành 2 phần: () và ()
Qua ta dựng một mặt phẳng song song với đáy hình hộp, mặt phẳng này cắt ở và cắt ở .
Ta có:
Do đó .
Chú ý: Có thể lí luận như sau: Giao điểm của các đường chéo của hình hộp là tâm đối xứng của hình hộp, do đó mặt phẳng chứa điểm nên chia hình hộp thành hai hình đối xứng với nhau qua điểm . Vậy hai hình này là hai hình bằng nhau và có thể tích bằng nhau.
Bài 12 trang 27 SGK Hình học 12: Cho hình lập phương cạnh . Gọi là trung điểm của là trung điểm của .
a) Tính thể tích khối tứ diện .
b) Mặt phẳng chia khối lập phương đã cho thành hai khối đa diện. Gọi là khối đa diện chứa đỉnh là khối đa diện còn lại. Tính tỉ số .
Phương pháp giải:
a) Coi khối tứ diện có đỉnh và đáy . Sử dụng công thức tính thể tích khối chóp:
b) Dựng thiết diện của hình lập phương khi cắt bởi mặt phẳng , xác định hai phần khối đa diện cẩn tính thể tích .
Lời giải:
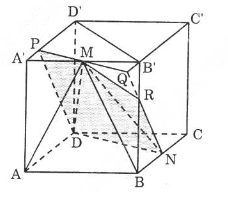
a) Ta tính thể tích hình chóp . Hình chóp này có chiều cao bằng khoảng cách từ M đến mặt phẳng (ANCD) bằng và diện tích đáy
b) Trước hết, ta dựng thiết diện của hình lập phương khi cắt bởi .
Do nên cắt theo một giao tuyến song song với . Ta dựng thiết diện như sau:
- Từ kẻ đường thẳng song song với , đường này cắt cạnh tại điểm và cắt đường thẳng tại điểm . Trong mặt phẳng thì cắt cạnh tại điểm ; đa giác chính là thiết diện của hình lập phương khi cắt bởi .
- Bây giờ ta tính thể tích khối đa diện . Ta có:
Hình chóp , có đường cao bằng , diện tích đáy là hình thang là:
Suy ra:
Dễ dàng chứng minh được và đồng dạng (g.g) nên
Hình chóp có chiều cao và diện tích hình thang là:
Suy ra:
Ta có:
Diện tích tam giác là:
Hình chóp có chiều cao và diện tích đáy nên:
Thể tích phần còn lại là:
Từ đây suy ra tỉ số cần tìm là:
(A) Số đỉnh và số mặt của một hình đa diện luôn bằng nhau;
(B) Tồn tại hình đa diện có số đỉnh và số mặt bằng nhau;
(C) Tồn tại một hình đa diện có số cạnh bằng số đỉnh;
(D) Tồn tại một hình đa diện có số cạnh và mặt bằng nhau.
Phương pháp giải:
Lấy ví dụ cho từng đáp án và sử dụng công thức p.Đ = 2C = nM.
Lời giải:
Hình lập phương có 8 đỉnh và 6 mặt nên đáp án A sai.
Xét hình tứ diện có 4 đỉnh và 4 mặt, nên đáp án B đúng.
Giả sử khối đa diện có số cạnh bằng số đỉnh Đ = C p = 2, tức là mỗi mặt có 2 cạnh (vô lí). Do đó đáp án C sai.
Giả sử khối đa diện có số cạnh bằng số mặt M = C n = 2, tức là mỗi đỉnh là đỉnh chung của 2 cạnh (vô lí). Do đó đáp án D sai.
Chọn đáp án (B).
Số các đỉnh hoặc số các mặt của bất kì hình đa diện nào cũng:
(A) Lớn hơn hoặc bằng 4; (B) Lớn hơn 4;
(C) Lớn hơn hoặc bằng 5; (D) Lớn hơn 5.
Phương pháp giải:
Nhớ lại hình đa diện là gì? Sự khác nhau giữa hình đa diện và đa giác?
Lời giải:
Chú ý: Đa giác là một đường gấp khúc khép kín, nghĩa là gồm những đoạn thẳng nối tiếp nhau (mỗi điểm nối là đầu mút của vừa đúng hai đoạn thẳng) cùng nằm trên một mặt phẳng và khép kín.
Hình đa diện là một số hữu hạn đa giác thỏa mãn hai điều kiện:
a) Hai đa giác bất kì hoặc không có điểm chung, hoặc có một đỉnh chung, hoặc có một cạnh chung.
b) Mỗi cạnh của một đa giác là cạnh chung của đúng hai đa giác.
Như vậy để tạo thành một hình đa diện ta cần ít nhất 3 điểm (tạo thành 1 mặt phẳng) và 1 điểm nằm ngoài mặt phẳng ấy.
Với 4 điểm này, tạo thành một hình tứ diện có 4 đỉnh và 4 mặt.
Dễ thấy hình tứ diện là hình đa diện có số mặt và số đỉnh nhỏ nhất trong các khối đa diện.
Chọn đáp án (A).
Số các cạnh của hình đa diện luôn luôn:
(A) Lớn hơn hoặc bằng 6;
(B) Lớn hơn 6;
(C) Lớn hơn 7;
(D) Lớn hơn hoặc bằng 8.
Phương pháp giải:
Lấy ví dụ khối tứ diện.
Lời giải:
Chú ý: Hình đa diện là một số hữu hạn đa giác thỏa mãn hai điều kiện:
a) Hai đa giác bất kì hoặc không có điểm chung, hoặc có một đỉnh chung, hoặc có một cạnh chung.
b) Mỗi cạnh của một đa giác là cạnh chung của đúng hai đa giác.
Như vậy để tạo thành một hình đa diện ta cần ít nhất 3 điểm (tạo thành 1 mặt phẳng) và 1 điểm nằm ngoài mặt phẳng ấy.
Với 4 điểm này, tạo thành một hình tứ diện có 4 đỉnh, 4 mặt và 6 cạnh.
Dễ thấy hình tứ diện là hình đa diện có số cạnh nhỏ nhất trong các khối đa diện.
Chọn (A).
(A) Khối tứ diện là khối đa diện lồi;
(B) Khối hộp là khối đa diện lồi;
(C) Lắp ghép hai khối hộp sẽ được một khối đa diện;
(D) Khối lăng trụ tam giác là khối đa diện lồi.
Phương pháp giải:
Khái niệm khối đa diện lồi: Khối đa diện được gọi là khối đa diện lồi nếu đoạn thẳng nối hai điểm bất kì của luôn thuộc .
Lời giải:
Dễ dàng nhận thấy các khối tứ diện, khối hộp, khối lăng trụ tam giác là các khối đa diện lồi. Do đó A, B, D đúng.
Khi lắp ghép hai khối hộp chưa chắc được một đa diện lồi. Ví dụ khi lắp ghép hai khối hộp như sau, ta không được một khối đa diện lồi.
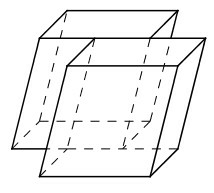
Chọn (C).
(A) Hai khối chóp có diện tích đáy và chiều cao tương ứng bằng nhau thì có thể tích bằng nhau.
(B) Hai khối hộp chữ nhật có diện tích toàn phần bằng nhau thì có thể tích bằng nhau.
(C) Hai khối lăng trụ có diện tích đáy và chiều cao tương ứng bằng nhau thì có thể tích bằng nhau.
(D) Hai khối lập phương có diện tích toàn phần bằng nhau thì có thể tích bằng nhau.
Phương pháp giải:
Suy luận từng đáp án, dựa váo các công thức tính thể tích, diện tích xung quanh, diện tích toàn phần của các khối đa diện.
Lời giải:
Ta có: nên đương nhiên khi hai khối chóp có diện tích đáy và chiều cao tương ứng bằng nhau thì có thể tích bằng nhau. A đúng.
Ta có: nên đương nhiên khi hai khối lăng trụ có diện tích đáy và chiều cao tương ứng bằng nhau thì có thể tích bằng nhau. C đúng.
Diện tích toàn phần của khối lập phương: , hai khối lập phương có diện tích toàn phần bằng nhau tức là có cạnh bằng nhau, , vậy chúng có thể tích bằng nhau. D đúng.
Chọn (B) Hai khối hộp chữ nhật có diện tích toàn phần bằng nhau thì chưa chắc có thể tích bằng nhau.
(A) (B)
(C) (D)
Phương pháp giải:
Sử dụng kết quả sau:
Cho khối chóp , trên các cạnh lấy các điểm . Khi đó ta có:
Lưu ý công thức trên chỉ được phép dùng đối với chóp tam giác, khi không là chóp tam giác phải sử dụng phân chia và lắp ghép các khối đa diện trước khi sử dụng công thức.
Lời giải:
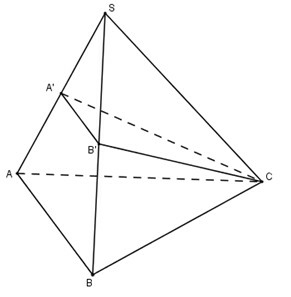
Ta có:
Chọn (C).
(A) (B)
(C) (D)
Phương pháp giải:
Cho khối chóp , trên các cạnh lấy các điểm . Khi đó ta có:
Lưu ý công thức trên chỉ được phép dùng đối với chóp tam giác, khi không là chóp tam giác phải sử dụng phân chia và lắp ghép các khối đa diện trước khi sử dụng công thức.
Lời giải:
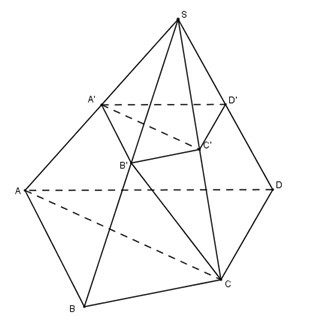
Ta có:
Chọn (C).
Chú ý và sai lầm: KHÔNG ĐƯỢC sử dụng công thức trên như sau: , đây là công thức SAI.
(A) (B)
(C) (D)
Phương pháp giải:
Khối lăng trụ tam giác đều là khối lăng trụ đứng có đáy là tam giác đều.
Lời giải:
Đáy của khối lăng trụ đều là tam giác đều cạnh nên ta có diện tích đáy:
Chiều cao của khối lăng trụ tam giác đều .
Vậy thể tích là:
Chọn (D).

