Giải Toán 12 Bài 5: Phương trình mũ và phương trình lôgarit

78 lượt xem

Bài trước

Bài sau

Chúng tôi giới thiệu Giải bài tập Toán lớp 12 Bài 5: Phương trình mũ và phương trình lôgarit chính xác, chi tiết nhất giúp học sinh dễ dàng làm bài tập Phương trình mũ và phương trình lôgarit lớp 12.

Giải bài tập Toán lớp 12 Bài 5: Phương trình mũ và phương trình lôgarit

Trả lời câu hỏi giữa bài

Trả lời câu hỏi 1 trang 80 SGK Giải tích 12: Giải phương trình

6^{2 x - 3} = 1

bằng cách đưa về dạng

a^{A (x)} = a^{B (x)}

và giải phương trình

A (x) = B (x) .

Lời giải:

$6^{(2 x - 3)} = 1 \Leftrightarrow 6^{(2 x - 3)} = 6^{0} \Leftrightarrow 2 x - 3 = 0 \Leftrightarrow x = \frac{3}{2}$

Trả lời câu hỏi 2 trang 81 SGK Giải tích 12: Giải phương trình:

\frac{1}{5} {.5}^{2 x} + {5.5}^{x} = 250

bằng cách đặt ẩn phụ

t = 5^{x}

Lời giải:

Đặt $t = 5^{x}$ , ta có:

$\begin{aligned} \frac{1}{5} t^{2} + 5 t = 250 \\ \Leftrightarrow t^{2} + 25 t - 1250 = 0 \\ \Leftrightarrow [\begin{matrix} t = 25 \\ t = - 50 (loại) \end{matrix} \\ \Leftrightarrow 5^{x} = 25 \Leftrightarrow x = 2 \end{aligned}$

Trả lời câu hỏi 3 trang 81 SGK Giải tích 12: Tính

x

, biết:

\log_{3} x = \frac{1}{4} .

Phương pháp giải:

Sử dụng định nghĩa logarit

\log_{a} x = n \Leftrightarrow x = a^{n}

Lời giải:

Theo định nghĩa logarit ta có: $x = 3^{\frac{1}{4}}$

Trả lời câu hỏi 4 trang 82 SGK Giải tích 12: Cho phương trình:

\log_{3} x + \log_{9} x = 6

Hãy đưa các logarit ở vế trái về cùng cơ số.

Phương pháp giải:

Sử dụng lý thuyết

\log_{a^{n}} b = \frac{1}{n} \log_{a} b

Lời giải:

$\log_{9} x = \log_{3^{2}} x = \frac{1}{2} \log_{3} x$

Vậy phương trình đã cho tương đương với phương trình:

$\log_{3} x + \frac{1}{2} . \log_{3} x = 6$

Trả lời câu hỏi 5 trang 83 SGK Giải tích 12: Giải phương trình:

(\log_{2} x)^{2} - 3 \log_{2} x + 2 = 0

bằng cách đặt ẩn phụ

t = \log_{2} x

Phương pháp giải:

- Thay $t = \log_{2} x$ vào phương trình đưa về phương trình ẩn $t$ .

- Giải phương trình tìm $t$ và suy ra $x$ .

Lời giải:

Với $t = \log_{2} x$ . Ta có phương trình đã cho tương đương với phương trình:

$\begin{aligned} t^{2} - 3 t + 2 = 0 \Leftrightarrow [\begin{matrix} t = 1 \\ t = 2 \end{matrix} \\ \Leftrightarrow [\begin{matrix} \log_{2} x = 1 \\ \log_{2} x = 2 \end{matrix} \Leftrightarrow [\begin{matrix} x = 2 \\ x = 4 \end{matrix} \end{aligned}$

Trả lời câu hỏi 6 trang 83 SGK Giải tích 12: Giải phương trình:

\log_{\frac{1}{2}} x + (\log_{2} x)^{2} = 2

Phương pháp giải:

Biến đổi các logarit về cùng cơ số

2

Lời giải:

$\begin{array}{l} \log_{\frac{1}{2}} x + {(\log_{2} x)}^{2} = 2 (ĐK : x > 0) \\ \Leftrightarrow \log_{2^{- 1}} x + {(\log_{2} x)}^{2} = 2 \\ \Leftrightarrow - \log_{2} x + {(\log_{2} x)}^{2} = 2 \\ \Leftrightarrow {(\log_{2} x)}^{2} - \log_{2} x - 2 = 0 \end{array}$

Đặt $t = \log_{2} x$ phương trình trở thành:

$t^{2} - t - 2 = 0 \Leftrightarrow [\begin{array}{l} t = - 1 \\ t = 2 \end{array}$

Với $t = - 1$ thì $\log_{2} x = - 1 \Leftrightarrow x = 2^{- 1} = \frac{1}{2} (T M)$

Với $t = 2$ thì $\log_{2} x = 2 \Leftrightarrow x = 2^{2} = 4 (T M)$

Vậy phương trình có tập nghiệm $S = {\frac{1}{2}; 4}$

Câu hỏi và bài tập (trang 84, 85 SGK Giải tích 12)

Bài 1 trang 84 SGK Giải tích 12: Giải các phương trình mũ:

a) ${(0, 3)}^{3 x - 2} = 1$ ;

{(\frac{1}{5})}^{x} = 25

;

2^{x^{2} - 3 x + 2} = 4

;

{(0, 5)}^{x + 7} . {(0, 5)}^{1 - 2 x} = 2

Phương pháp giải:

+) Sử dụng các công thức của hàm lũy thừa: $a^{m} . a^{n} = a^{m + n}; \frac{a^{m}}{a^{n}} = a^{m - n}; a^{0} = 1.$

+) Đưa phương trình về dạng: $a^{f (x)} = a^{g (x)} \Leftrightarrow f (x) = g (x) (*)$ sau đó giải phương trình (*) tìm nghiệm của phương trình rồi kết luận nghiệm.

Lời giải:

${(0, 3)}^{3 x - 2} = 1 \Leftrightarrow {(0, 3)}^{3 x - 2} = {(0, 3)}^{0} \Leftrightarrow 3 x - 2 = 0 \Leftrightarrow x = \frac{2}{3} .$

Vậy phương trình có nghiệm: $x = \frac{2}{3} .$

$\begin{array}{l} {(\frac{1}{5})}^{x} = 25 \Leftrightarrow \frac{1}{5^{x}} = 5^{2} \\ \Leftrightarrow 5^{- x} = 5^{2} \Leftrightarrow x = - 2 \end{array}$

Vậy phương trình có nghiệm $x = - 2.$

$2^{x^{2} - 3 x + 2} = 4 \Leftrightarrow 2^{x^{2} - 3 x + 2} = 2^{2} \Leftrightarrow x^{2} - 3 x + 2 = 2 \Leftrightarrow x^{2} - 3 x = 0 \Leftrightarrow [\begin{array}{l} x = 0 \\ x = 3 \end{array} .$

Vậy phương trình có nghiệm $x = 0$ hoặc $x = 3.$

${(0, 5)}^{x + 7} . {(0, 5)}^{1 - 2 x} = 2 \Leftrightarrow {(\frac{1}{2})}^{x + 7} . {(\frac{1}{2})}^{1 - 2 x} = 2 \Leftrightarrow {(\frac{1}{2})}^{x + 7 + 1 - 2 x} = 2 \Leftrightarrow {(\frac{1}{2})}^{- x + 8} = 2 \Leftrightarrow 2^{x - 8} = 2^{1} \Leftrightarrow x - 8 = 1 \Leftrightarrow x = 9.$

Vậy phương trình có nghiệm $x = 9.$

Bài 2 trang 84 SGK Giải tích 12: Giải các phương trình mũ:

3^{2 x - 1} + 3^{2 x} = 108

;

2^{x + 1} + 2^{x - 1} + 2^{x} = 28

;

64^{x} - 8^{x} - 56 = 0

;

{3.4}^{x} - {2.6}^{x} = 9^{x}

Phương pháp giải:

+) Sử dụng các công thức cơ bản của hàm lũy thừa, biến đổi phương trình về các dạng cơ bản sau đó giải phương trình.

+) Đưa phương trình về dạng: $a^{f (x)} = a^{g (x)} \Leftrightarrow f (x) = g (x) .$

+) Giải các phương trình bằng phương pháp đổi biến.

+) Khi đổi biến nhớ đặt điều kiện cho biến mới.

+) Giải phương trình tìm biến mới, đối chiếu với điều kiện đã đặt. Sau đó quay lại giải phương trình tìm ẩn x ban đầu.

Lời giải:

$\begin{array}{l} 3^{2 x - 1} + 3^{2 x} = 108 \\ \Leftrightarrow \frac{1}{3} {.3}^{2 x} + 3^{2 x} = 108 \\ \Leftrightarrow \frac{4}{3} {.3}^{2 x} = 108 \\ \Leftrightarrow 3^{2 x} = 81 \\ \Leftrightarrow 3^{2 x} = 3^{4} \\ \Leftrightarrow 2 x = 4 \\ \Leftrightarrow x = 2. \end{array}$

Vậy phương trình có nghiệm $x = 2$ .

$\begin{array}{l} 2^{x + 1} + 2^{x - 1} + 2^{x} = 28 \\ \Leftrightarrow {2.2}^{x} + \frac{1}{2} {.2}^{x} + 2^{x} = 28 \\ \Leftrightarrow \frac{7}{2} {.2}^{x} = 28 \\ \Leftrightarrow 2^{x} = 8 \\ \Leftrightarrow 2^{x} = 2^{3} \\ \Leftrightarrow x = 3. \end{array}$

Vậy phương trình có nghiệm $x = 3.$

$\begin{array}{l} c) 64^{x} - 8^{x} - 56 = 0 \\ \Leftrightarrow {(8^{x})}^{2} - 8^{x} - 56 = 0. \end{array}$

Đặt $8^{x} = t (t > 0) .$ Khi đó ta có:
$\begin{array}{l} P t \Leftrightarrow t^{2} - t - 56 = 0 \\ \Leftrightarrow (t - 8) (t + 7) = 0 \\ \Leftrightarrow [\begin{array}{l} t - 8 = 0 \\ t + 7 = 0 \end{array} \Leftrightarrow [\begin{array}{l} t = 8 (t m) \\ t = - 7 (k t m) \end{array} . \\ \Rightarrow 8^{x} = 8 \Leftrightarrow x = 1. \end{array}$
Vậy phương trình có nghiệm $x = 1.$

$P T \Leftrightarrow {3.4}^{x} - {2.6}^{x} - 9^{x} = 0$

Chia cả 2 vế của pt cho $9^{x} > 0$ ta được:

$\begin{array}{l} 3. \frac{4^{x}}{9^{x}} - 2. \frac{6^{x}}{9^{x}} - 1 = 0 \\ \Leftrightarrow 3. {(\frac{4}{9})}^{x} - 2. {(\frac{6}{9})}^{x} - 1 = 0 \\ \Leftrightarrow 3. {[{(\frac{2}{3})}^{x}]}^{2} - 2. {(\frac{2}{3})}^{x} - 1 = 0 \end{array}$

Đặt ${(\frac{2}{3})}^{x} = t (t > 0) .$ Khi đó ta có:
$\begin{array}{l} p t \Leftrightarrow 3 t^{2} - 2 t - 1 = 0 \\ \Leftrightarrow (3 t + 1) (t - 1) = 0 \\ \Leftrightarrow [\begin{array}{l} 3 t + 1 = 0 \\ t - 1 = 0 \end{array} \Leftrightarrow [\begin{array}{l} t = - \frac{1}{3} (k t m) \\ t = 1 (t m) \end{array} \\ \Rightarrow {(\frac{2}{3})}^{x} = 1 \Leftrightarrow x = 0. \end{array}$
Vậy phương trình có nghiệm $x = 0.$

Bài 3 trang 84 SGK Giải tích 12: Giải các phương trình logarit

a) $\log_{3} (5 x + 3) = \log_{3} (7 x + 5)$

\log (x - 1) - \log (2 x - 11) = \log 2

\log_{2} (x - 5) + \log_{2} (x + 2) = 3

\log (x^{2} - 6 x + 7) = \log (x - 3)

Phương pháp giải:

+) Tìm điều kiện xác định.

+) Đưa về cùng cơ số: $\log_{a} f (x) = \log_{a} g (x) \Leftrightarrow {\begin{cases} f (x) > 0 \\ g (x) > 0 \\ f (x) = g (x) \end{cases}$

Lời giải:

$\log_{3} (5 x + 3) = \log_{3} (7 x + 5)$ (1)

$D K : {\begin{cases} 5 x + 3 > 0 \\ 7 x + 5 > 0 \end{cases} \Leftrightarrow {\begin{cases} x > - \frac{3}{5} \\ x > - \frac{5}{7} \end{cases}$ $\Leftrightarrow x > - \frac{3}{5}$

TXĐ: $D = (\frac{- 3}{5}, + \infty)$

Khi đó: (1) $\Rightarrow 5 x + 3 = 7 x + 5$ $\Leftrightarrow 2 x = - 2 \Leftrightarrow x = - 1$ (loại)

Vậy phương trình (1) vô nghiệm.

$\log (x - 1) - \log (2 x - 11) = \log 2$ (2)

$D K : {\begin{cases} x - 1 > 0 \\ 2 x - 11 > 0 \end{cases} \Leftrightarrow {\begin{cases} x > 1 \\ x > \frac{11}{2} \end{cases}$ $\Leftrightarrow x > \frac{11}{2}$

TXĐ: $D = (\frac{11}{2}; + \infty) .$

Khi đó: $(2) \Rightarrow \log \frac{x - 1}{2 x - 11} = \log 2$ $\Leftrightarrow \frac{x - 1}{2 x - 11} = 2$ $\Rightarrow x - 1 = 4 x - 22 \Leftrightarrow 3 x = 21$ $\Leftrightarrow x = 7 (T M)$

Vậy phương trình có nghiệm là $x = 7.$

$\log_{2} (x - 5) + \log_{2} (x + 2) = 3$ (3)

$D K : {\begin{cases} x - 5 > 0 \\ x + 2 > 0 \end{cases}$ $\Leftrightarrow {\begin{cases} x > 5 \\ x > - 2 \end{cases} \Leftrightarrow x > 5$

TXĐ: $(5; + \infty)$

Khi đó:

$(3) \Leftrightarrow \log_{2} [(x - 5) (x + 2)] = 3$

$\Leftrightarrow (x - 5) (x + 2) = 2^{3}$

$\Leftrightarrow x^{2} - 3 x - 10 = 8$

$\Leftrightarrow x^{2} - 3 x - 18 = 0 \Leftrightarrow (x - 6) (x + 3) = 0 \Leftrightarrow [\begin{matrix} x - 6 = 0 \\ x + 3 = 0 \end{matrix} \Leftrightarrow [\begin{matrix} x = 6 (t m) \\ x = - 3 (k t m) \end{matrix}$

Vậy phương trình có nghiệm $x = 6$

$\log_{} (x^{2} - 6 x + 7) = \log (x - 3)$ (4)

$D K : {\begin{cases} x^{2} - 6 x + 7 > 0 \\ x - 3 > 0 \end{cases}$ $\Leftrightarrow {\begin{cases} [\begin{array}{l} x > 3 + \sqrt{2} \\ x < 3 - \sqrt{2} \end{array} \\ x > 3 \end{cases}$ $\Leftrightarrow x > 3 + \sqrt{2}$

TXĐ: $D = (3 + \sqrt{2}, + \infty)$

Khi đó:

$\begin{array}{l} (4) \Leftrightarrow x^{2} - 6 x + 7 = x - 3 \\ \Leftrightarrow x^{2} - 7 x + 10 = 0 \\ \Leftrightarrow (x - 5) (x - 2) = 0 \\ \Leftrightarrow [\begin{array}{l} x - 5 = 0 \\ x - 2 = 0 \end{array} \Leftrightarrow [\begin{array}{l} x = 5 (t m) \\ x = 2 (k t m) \end{array} . \end{array}$

Vậy phương trình có nghiệm là $x = 5$ .

Bài 4 trang 85 SGK Giải tích 12: Giải các phương trình lôgarit:

a) $\frac{1}{2} \log (x^{2} + x - 5) = \log 5 x + \log \frac{1}{5 x}$

b) $\frac{1}{2} . \log (x^{2} - 4 x - 1) = \log 8 x - \log 4 x$

\log_{\sqrt{2}} x + 4 \log_{4} x + \log_{8} x = 13

Phương pháp giải:

Các bước giải phương trình logarit:

+) Tìm điều kiện xác định.

+) Sử dụng các phương pháp tương ứng để giải phương trình (có các phương pháp: đưa về cùng cơ số, đặt ẩn phụ, mũ hóa….).

+) Giải phương trình để tìm ẩn và so sánh với điều kiện xác định rồi kết luận nghiệm của phương trình.

Bài toán này chủ yếu sử dụng phương pháp đưa về cùng cơ số: $\log_{a} f (x) = \log_{a} g (x) \Leftrightarrow {\begin{cases} f (x) > 0 \\ g (x) > 0 \\ f (x) = g (x) \end{cases} .$

Chú ý: $\log a + \log b = \log a b$ ; $\log a - \log b = \log \frac{a}{b}$

Lời giải:

$\frac{1}{2} \log (x^{2} + x - 5) = \log 5 x + \log \frac{1}{5 x} .$

Điều kiện: ${\begin{cases} x^{2} + x - 5 > 0 \\ 5 x > 0 \\ \frac{1}{5 x} > 0 \end{cases} \Leftrightarrow {\begin{cases} [\begin{array}{l} x > \frac{- 1 + \sqrt{21}}{2} \\ x < \frac{- 1 - \sqrt{21}}{2} \end{array} \\ x > 0 \end{cases}$ $\Leftrightarrow x > \frac{- 1 + \sqrt{21}}{2} \approx 1, 79.$

$\begin{array}{l} P t \Leftrightarrow \frac{1}{2} . \log (x^{2} + x - 5) = \log (5 x . \frac{1}{5 x}) \\ \Leftrightarrow \frac{1}{2} . \log (x^{2} + x - 5) = \log 1 \\ \Leftrightarrow \log (x^{2} + x - 5) = 0 \\ \Leftrightarrow x^{2} + x - 5 = 10^{0} = 1 \\ \Leftrightarrow x^{2} + x - 6 = 0 \\ \Leftrightarrow (x + 3) (x - 2) = 0 \\ \Leftrightarrow [\begin{array}{l} x + 3 = 0 \\ x - 2 = 0 \end{array} \Leftrightarrow [\begin{array}{l} x = - 3 (k t m) \\ x = 2 (t m) \end{array} . \end{array}$

Vậy phương trình có nghiệm $x = 2$ .

$\frac{1}{2} . \log (x^{2} - 4 x - 1) = \log 8 x - \log 4 x .$

Điều kiện: ${\begin{cases} x^{2} - 4 x - 1 > 0 \\ 8 x > 0 \\ 4 x > 0 \end{cases}$ $\Leftrightarrow {\begin{cases} [\begin{array}{l} x > 2 + \sqrt{5} \\ x < 2 - \sqrt{5} \end{array} \\ x > 0 \end{cases}$ $\Leftrightarrow x > 2 + \sqrt{5} .$

$\begin{array}{l} P t \Leftrightarrow \frac{1}{2} . \log (x^{2} - 4 x - 1) = \log \frac{8 x}{4 x} \\ \Leftrightarrow \log \sqrt{x^{2} - 4 x - 1} = \log 2 \\ \Leftrightarrow \sqrt{x^{2} - 4 x - 1} = 2 \\ \Leftrightarrow x^{2} - 4 x - 1 = 4 \\ \Leftrightarrow x^{2} - 4 x - 5 = 0 \\ \Leftrightarrow (x + 1) (x - 5) = 0 \\ \Leftrightarrow [\begin{array}{l} x + 1 = 0 \\ x - 5 = 0 \end{array} \Leftrightarrow [\begin{array}{l} x = - 1 (k t m) \\ x = 5 (t m) \end{array} . \end{array}$

Vậy phương trình có nghiệm $x = 5.$

$\log_{\sqrt{2}} x + 4 \log_{4} x + \log_{8} x = 13.$

Điều kiện: $x > 0.$

$\begin{array}{l} P t \Leftrightarrow \log_{2^{\frac{1}{2}}} x + 4 \log_{2^{2}} x + \log_{2^{3}} x = 13 \\ \Leftrightarrow 2 \log_{2} x + 4. \frac{1}{2} . \log_{x} x + \frac{1}{3} . \log_{2} x = 13 \\ \Leftrightarrow \frac{13}{3} . \log_{2} x = 13 \\ \Leftrightarrow \log_{2} x = 3 \\ \Leftrightarrow x = 2^{3} = 8 (t m) . \end{array}$

Vậy phương trình có nghiệm $x = 8.$

Lý thuyết Bài 5: Phương trình mũ và phương trình lôgarit

I. PHƯƠNG TRÌNH MŨ

1. Phương trình mũ cơ bản

Phương trình có dạng $a^{x} = b (0 < a \neq 1)$

+) Với $b > 0$ ta có $a^{x} = b \Leftrightarrow x = \log_{a} b$ .

+) Với $b \leq 0$ phương trình vô nghiệm.

Ví dụ: Giải phương trình $5^{x} = 125$ .

Ta có:

$\begin{array}{l} 5^{x} = 125 \\ \Leftrightarrow x = \log_{5} 125 \\ \Leftrightarrow x = 3 \end{array}$

2. Cách giải một số phương trình mũ đơn giản

a) Đưa về cùng cơ số

Ví dụ: Giải phương trình ${(\frac{1}{2})}^{2 x - 1} = 2^{3 x}$

Ta có:

$\begin{array}{l} {(\frac{1}{2})}^{2 x - 1} = 2^{3 x} \\ \Leftrightarrow 2^{- 2 x + 1} = 2^{3 x} \\ \Leftrightarrow - 2 x + 1 = 3 x \\ \Leftrightarrow 1 = 5 x \\ \Leftrightarrow x = \frac{1}{5} \end{array}$

b) Đặt ẩn phụ

Ví dụ: Giải phương trình $4^{x} - 2^{x + 1} + 1 = 0$ .

Ta có:

$\begin{array}{l} 4^{x} - 2^{x + 1} + 1 = 0 \\ \Leftrightarrow {(2^{x})}^{2} - {2.2}^{x} + 1 = 0 \end{array}$

Đặt $t = 2^{x} > 0$ ta được:

$\begin{array}{l} t^{2} - 2 t + 1 = 0 \\ \Leftrightarrow {(t - 1)}^{2} = 0 \\ \Leftrightarrow t - 1 = 0 \\ \Leftrightarrow t = 1 \end{array}$

$\begin{array}{l} \Rightarrow 2^{x} = 1 \\ \Leftrightarrow x = \log_{2} 1 \\ \Leftrightarrow x = 0 \end{array}$

c) Logarit hóa

Ví dụ: Giải phương trình $3^{x} {.2}^{x^{2}} = 1$ .

Logarit hai vế cơ số $3$ ta được:

$\begin{array}{l} \log_{3} (3^{x} {.2}^{x^{2}}) = \log_{3} 1 \\ \Leftrightarrow \log_{3} 3^{x} + \log_{3} 2^{x^{2}} = 0 \\ \Leftrightarrow x + x^{2} \log_{3} 2 = 0 \\ \Leftrightarrow x (1 + x \log_{3} 2) = 0 \\ \Leftrightarrow [\begin{array}{l} x = 0 \\ 1 + x \log_{3} 2 = 0 \end{array} \\ \Leftrightarrow [\begin{array}{l} x = 0 \\ x = - \frac{1}{\log_{3} 2} = - \log_{2} 3 \end{array} \end{array}$

d) Đưa về phương trình tích.

Phương pháp:

- Bước 1: Tìm điều kiện xác định (nếu có)

- Bước 2: Biến đổi phương trình về dạng tích $A B = 0 \Leftrightarrow [\begin{array}{l} A = 0 \\ B = 0 \end{array}$

- Bước 3: Giải các phương trình $A = 0, B = 0$ tìm nghiệm.

- Bước 4: Kiểm tra điều kiện và kết luận nghiệm.

e) Sử dụng bất đẳng thức, tính đơn điệu của hàm số.

Phương pháp:

- Bước 1: Tìm điều kiện xác định.

- Bước 2: Có thể làm một trong hai cách sau:

Cách 1: Biến đổi phương trình sao cho một vế là hàm số đơn điệu, một vế là hằng số hoặc một vế là hàm đồng biến và vế còn lại là hàm số nghịch biến.

Cách 2: Biến đổi phương trình về dạng $f (u) = f (v)$ với $f$ là hàm số đơn điệu.

- Bước 3: Nhẩm một nghiệm của phương trình trên.

- Bước 4: Kết luận nghiệm duy nhất của phương trình.

II. PHƯƠNG TRÌNH LOGARIT

1. Phương trình logarit cơ bản

Phương trình có dạng $\log_{a} x = b$ $(0 < a \neq 1)$

Ta có: $\log_{a} x = b \Leftrightarrow x = a^{b}$ .

Phương trình luôn có nghiệm $x = a^{b}$ .

Ví dụ: Giải phương trình $\log_{5} x = - 2$ .

Ta có: $\log_{5} x = - 2 \Leftrightarrow x = 5^{- 2} \Leftrightarrow x = \frac{1}{25}$ .

2. Cách giải một số phương trình logarit

a) Đưa về cùng cơ số

Ví dụ: Giải phương trình $\log_{2} x + \log_{4} x = 1$

Ta có:

$\begin{array}{l} \log_{2} x + \log_{4} x = 1 \\ \Leftrightarrow \log_{2} x + \frac{1}{2} \log_{2} x = 1 \\ \Leftrightarrow \frac{3}{2} \log_{2} x = 1 \\ \Leftrightarrow \log_{2} x = \frac{2}{3} \\ \Leftrightarrow x = 2^{\frac{2}{3}} \\ \Leftrightarrow x = \sqrt[3]{4} \end{array}$

b) Đặt ẩn phụ

Ví dụ: Giải phương trình $\frac{1}{\ln x} + \frac{1}{\ln x - 1} = \frac{5}{6}$ .

ĐK: ${\begin{cases} x > 0 \\ \ln x \neq 0 \\ \ln x \neq 1 \end{cases} \Leftrightarrow {\begin{cases} x > 0 \\ x \neq 1 \\ x \neq e \end{cases}$

Đặt $t = \ln x (t \neq 0, t \neq 1)$ ta được:

$\begin{array}{l} \frac{1}{t} + \frac{1}{t - 1} = \frac{5}{6} \\ \Leftrightarrow \frac{6 t - 6 + 6 t}{6 t (t - 1)} = \frac{5 t (t - 1)}{6 t (t - 1)} \\ \Rightarrow 12 t - 6 = 5 t^{2} - 5 t \\ \Leftrightarrow 5 t^{2} - 17 t + 6 = 0 \\ \Leftrightarrow [\begin{array}{l} t = 3 \\ t = \frac{2}{5} \end{array} (T M) \\ \Rightarrow [\begin{array}{l} \ln x = 3 \\ \ln x = \frac{2}{5} \end{array} \\ \Leftrightarrow [\begin{array}{l} x = e^{3} \\ x = e^{\frac{2}{5}} \end{array} (T M) \end{array}$

Vậy phương trình có tập nghiệm $S = {e^{3}; e^{\frac{2}{5}}}$ .

c) Mũ hóa

Ví dụ: Giải phương trình $\log_{3} (3 - 3^{x}) = 1 + x$

ĐK: $3 - 3^{x} > 0 \Leftrightarrow 3^{x} < 3 \Leftrightarrow x < 1$

Ta có:

$\begin{array}{l} \log_{3} (3 - 3^{x}) = 1 + x \\ \Leftrightarrow 3 - 3^{x} = 3^{1 + x} \\ \Leftrightarrow 3 - 3^{x} = {3.3}^{x} \\ \Leftrightarrow 3 = {4.3}^{x} \\ \Leftrightarrow 3^{x} = \frac{3}{4} \\ \Leftrightarrow x = \log_{3} \frac{3}{4} \\ \Leftrightarrow x = 1 - \log_{3} 4 (T M) \end{array}$

d) Đưa về phương trình tích.

Phương pháp:

- Bước 1: Tìm điều kiện xác định (nếu có)

- Bước 2: Biến đổi phương trình về dạng tích $A B = 0 \Leftrightarrow [\begin{array}{l} A = 0 \\ B = 0 \end{array}$

- Bước 3: Giải các phương trình $A = 0, B = 0$ tìm nghiệm.

- Bước 4: Kiểm tra điều kiện và kết luận nghiệm.

e) Sử dụng bất đẳng thức, tính đơn điệu của hàm số.

Phương pháp:

- Bước 1: Tìm điều kiện xác định.

- Bước 2: Có thể làm một trong hai cách sau:

Cách 2: Biến đổi phương trình về dạng $f (u) = f (v)$ với $f$ là hàm số đơn điệu.

- Bước 3: Nhẩm một nghiệm của phương trình trên.

- Bước 4: Kết luận nghiệm duy nhất của phương trình.

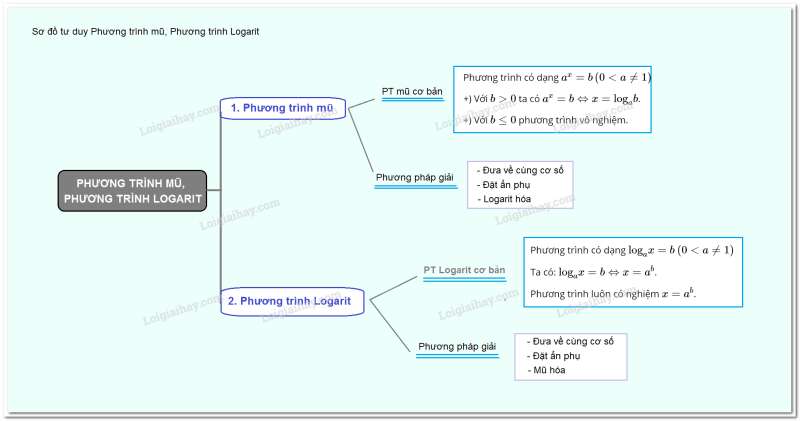
Sơ đồ tư duy về phương trình mũ và phương trình logarit

Phương pháp giải hệ phương trình mũ và logarit

Dạng 1: Giải hệ phương trình bằng phương pháp biến đổi tương đương.

Phương pháp:

- Bước 1: Đặt điều kiện cho ẩn để các biểu thức trong hệ có nghĩa.

- Bước 2: Dùng các biến đổi tương đương (rút thế, công đại số,…) để nhận được phương trình 1 ẩn.

- Bước 3: Giải các phương trình một ẩn nhận được từ hệ.

- Bước 4: Kiểm tra điều kiện và kết luận nghiệm.

Dạng 2: Giải hệ phương trình bằng phương pháp đặt ẩn phụ.

Phương pháp:

- Bước 1: Đặt điều kiện cho các biểu thức trong hệ có nghĩa.

- Bước 2: Lựa chọn ẩn phụ để biến đổi hệ ban đầu về hệ đại số đã biết (hệ đối xứng loại 1, loại 2, hệ đẳng cấp,…)

- Bước 3: Giải hệ.

- Bước 4: Kiểm tra điều kiện và kết luận nghiệm.

Dạng 3: Giải hệ phương trình bằng phương pháp hàm.

- Bước 1: Đặt điều kiện cho các biểu thức trong hệ có nghĩa.

- Bước 2: Rút ra từ hệ một phương trình dạng $f (x) = f (y)$ .

- Bước 3: Sử dụng phương pháp hàm số: Nếu hàm số $f (t)$ đơn điệu trong khoảng đang xét thì phương trình $f (x) = f (y)$ có nghiệm duy nhất $x = y$ .

- Bước 4: Thay $y = x$ vào phương trình còn lại trong hệ, giải phương trình đó.

- Bước 5: Kiểm tra điều kiện và kết luận nghiệm.

Xem thêm các chương trình khác:

Bài trước

Bài sau

Giải SGK, SBT, Chuyên đề Toán Học Lớp 12

Giải Toán 12 Bài 5: Phương trình mũ và phương trình lôgarit

Xem thêm các chương trình khác: