Giải Toán 12 Bài 3: Lôgarit

74 lượt xem

Bài trước

Bài sau

Chúng tôi giới thiệu Giải bài tập Toán lớp 12 Bài 3: Lôgarit chính xác, chi tiết nhất giúp học sinh dễ dàng làm bài tập Lôgarit lớp 12.

Bài giảng Toán học 12 Bài 3: Lôgarit

Giải bài tập Toán lớp 12 Bài 3: Lôgarit

Trả lời câu hỏi giữa bài

Trả lời câu hỏi 1 trang 61 SGK Giải tích 12: Tìm x để:

$\begin{aligned} a) 2^{x} = 8 \end{aligned}$

$\begin{aligned} b) 2^{x} = \frac{1}{4} \end{aligned}$

$\begin{aligned} c) 3^{x} = 81 \end{aligned}$

$\begin{aligned} d) 5^{x} = \frac{1}{125} \end{aligned}$

Phương pháp giải:

Sử dụng lý thuyết $a^{m} = a^{n} \Leftrightarrow m = n$ với điều kiện các biểu thức đều có nghĩa.

Lời giải:

$\begin{aligned} 2^{x} = 8 \Leftrightarrow 2^{x} = 2^{3} \Leftrightarrow x = 3 \end{aligned}$

$\begin{aligned} 2^{x} = \frac{1}{4} \Leftrightarrow 2^{x} = 2^{- 2} \Leftrightarrow x = - 2 \end{aligned}$

$\begin{aligned} 3^{x} = 81 \Leftrightarrow 3^{x} = 3^{4} \Leftrightarrow x = 4 \end{aligned}$

$\begin{aligned} 5^{x} = \frac{1}{125} \Leftrightarrow 5^{x} = 5^{- 3} \Leftrightarrow x = - 3 \end{aligned}$

Trả lời câu hỏi 2 trang 62 SGK Giải tích 12: a) Tính

\log_{\frac{1}{2}} 4, \log_{3} \frac{1}{27}

b) Có các số

x, y

nào để

3^{x} = 0, 2^{y} = - 3

hay không?

Phương pháp giải:

a) Tìm một số thực $x$ thỏa mãn ${(\frac{1}{2})}^{x} = 4$ .

Tìm một số thực thỏa mãn $3^{x} = \frac{1}{27}$

b) Nhận xét giá trị của

3^{x}

và

2^{y}

suy ra kết luận.

Lời giải:

$\log_{\frac{1}{2}} 4 = - 2$ vì ${(\frac{1}{2})}^{- 2} = \frac{1}{2^{- 2}} = 4$

$\log_{3} \frac{1}{27} = - 3$ vì $3^{- 3} = \frac{1}{3^{3}} = \frac{1}{27}$

Không có số $x, y$ nào để $3^{x} = 0; 2^{y} = - 3$ vì $3^{x} > 0; 2^{y} > 0$ với mọi $x, y$ .

Trả lời câu hỏi 3 trang 62 SGK Giải tích 12: Hãy chứng minh các tính chất:

$\begin{array}{l} \log_{a} 1 = 0, \log_{a} a = 1 \\ a^{\log_{a} b} = b, \log_{a} (a^{α}) = α \end{array}$

Phương pháp giải:

Sử dụng định nghĩa

α = \log_{a} b \Leftrightarrow b = a^{α}

Lời giải:

Ta có:

$a^{0} = 1 \Leftrightarrow 0 = \log_{a} 1$ .

$a^{1} = a \Leftrightarrow 1 = \log_{a} a$ .

Đặt $α = \log_{a} b$ . Từ điịnh nghĩa logarit ta có:

$α = \log_{a} b \Leftrightarrow b = a^{α} = a^{\log_{a} b}$

$\Rightarrow b = a^{\log_{a} b}$

Đặt $\log_{a} a^{α} = b$

Theo định nghĩa $a^{α} = a^{b} \Rightarrow α = b$

Vậy $\log_{a} a^{α} = b = α$ .

Trả lời câu hỏi 4 trang 63 SGK Giải tích 12: Tính:

4^{\log_{2} \frac{1}{7}}; {(\frac{1}{25})}^{\log_{5} \frac{1}{3}}

Phương pháp giải:

Sử dụng các công thức

{(a^{m})}^{n} = {(a^{n})}^{m}; a^{\log_{a} b} = b

Lời giải:

$\begin{aligned} 4^{\log_{2} \frac{1}{7}} = 2^{2 \log_{2} \frac{1}{7}} \\ = {(2^{\log_{2} \frac{1}{7}})}^{2} = {(\frac{1}{7})}^{2} = \frac{1}{49} \\ {(\frac{1}{25})}^{\log_{5} \frac{1}{3}} = 5^{- 2 \log_{5} \frac{1}{3}} = {(5^{^{\log_{5} \frac{1}{3}}})}^{- 2} \\ = {(\frac{1}{3})}^{- 2} = 9 \end{aligned}$

Trả lời câu hỏi 5 trang 63 SGK Giải tích 12: Cho

b_{1} = 2^{3}; b_{2} = 2^{5}

Tính $\log_{2} b_{1} + \log_{2} b_{2}; \log_{2} b_{1} b_{2}$ và so sánh các kết quả.

Phương pháp giải:

Sử dụng công thức

\log_{a} a^{n} = n

và

\log_{a} (b c) = \log_{a} b + \log_{a} c

Lời giải:

$\begin{aligned} \log_{2} b_{1} + \log_{2} b_{2} = \log_{2} 2^{3} + \log_{2} 2^{5} = 3 + 5 = 8 \\ \log_{2} b_{1} b_{2} = \log_{2} (2^{3} {.2}^{5}) = \log (2^{3 + 5}) = \log_{2} 2^{8} = 8 \end{aligned}$

Vậy $\log_{2} b_{1} + \log_{2} b_{2} = \log_{2} b_{1} b_{2}$

Trả lời câu hỏi 6 trang 64 SGK Giải tích 12: Tính:

$\log_{\frac{1}{2}} 2 + 2 \log_{\frac{1}{2}} \frac{1}{3} + \log_{\frac{1}{2}} \frac{3}{8}$

Phương pháp giải:

Sử dụng công thức logarit của một tích

$\log_{a} b_{1} + \log_{a} b_{2} + . . . + \log_{a} b_{n}$ $= \log_{a} (b_{1} b_{2} . . . b_{n})$

Lời giải:

$\begin{aligned} \log_{\frac{1}{2}} 2 + 2 \log_{\frac{1}{2}} \frac{1}{3} + \log_{\frac{1}{2}} \frac{3}{8} \\ = \log_{\frac{1}{2}} 2 + \log_{\frac{1}{2}} \frac{1}{3} + \log_{\frac{1}{2}} \frac{1}{3} + \log_{\frac{1}{2}} \frac{3}{8} \\ = \log_{\frac{1}{2}} (2. \frac{1}{3} . \frac{1}{3} . \frac{3}{8}) = \log_{\frac{1}{2}} \frac{1}{12} \end{aligned}$

Trả lời câu hỏi 7 trang 64 SGK Giải tích 12: Cho

b_{1} = 2^{5}; b_{2} = 2^{3}

. Tính

\log_{2} b_{1} - \log_{2} b_{2}; \log_{2} \frac{b_{1}}{b_{2}}

và so sánh các kết quả.

Lời giải:

$\begin{aligned} \log_{2} b_{1} - \log_{2} b_{2} = \log_{2} 2^{5} - \log_{2} 2^{3} \\ = 5 - 3 = 2 \\ \log_{2} \frac{b_{1}}{b_{2}} = \log_{2} \frac{2^{5}}{2^{3}} = \log_{2} 2^{2} = 2 \\ \Rightarrow \log_{2} b_{1} - \log_{2} b_{2} = \log_{2} \frac{b_{1}}{b_{2}} \end{aligned}$

Trả lời câu hỏi 8 trang 65 SGK Giải tích 12: Cho

a = 4, b = 64, c = 2.

Tính

\log_{a} b; \log_{c} a; \log_{c} b

Tìm một hệ thức liên hệ giữa ba kết quả thu được.

Lời giải:

$\begin{aligned} \log_{a} b = \log_{4} 64 = \log_{4} 4^{3} = 3 \\ \log_{c} a = \log_{2} 4 = \log_{2} 2^{2} = 2 \\ \log_{c} b = \log_{2} 64 = \log_{2} 2^{6} = 6 \\ 3.2 = 6 \Rightarrow \log_{a} b . \log_{c} a = \log_{c} b \end{aligned}$

Câu hỏi và bài tập (trang 68 SGK Giải tích 12)

Bài 1 trang 68 SGK Giải tích 12: Không sử dụng máy tính, hãy tính:

a) $\log_{2} \frac{1}{8}$ ;

\log_{\frac{1}{4}} 2

;

\log_{3} \sqrt[4]{3}

;

\log_{0, 5} 0, 125

Phương pháp giải:

+) Sử dụng các công thức của logarit: $\log_{a} a = 1; \log_{a} b^{n} = n \log_{a} b;$ $\log_{a^{m}} b = \frac{1}{m} \log_{a} b; \log_{a} b = \frac{\log_{c} b}{\log_{c} a} .$

Lời giải:

$\log_{2} \frac{1}{8} = \log_{2} 2^{- 3} = - 3 \log_{2} 2 = - 3$ .

$\log_{\frac{1}{4}} 2 = \log_{2^{- 2}} 2 = \frac{1}{- 2} . \log_{2} 2 = - \frac{1}{2}$ .

hoặc dùng công thức đổi cơ số : $\log_{\frac{1}{4}} 2 = \frac{\log_{2} 2}{\log_{2} \frac{1}{4}} = \frac{1}{\log_{2} 2^{- 2}} = - \frac{1}{2}$ .

$\log_{3} \sqrt[4]{3} = \log_{3} 3^{\frac{1}{4}} = \frac{1}{4} . \log_{3} 3 = \frac{1}{4}$ .

$\log_{0, 5} 0, 125 = \log_{0, 5} 0, 5^{3}$ $= 3. \log_{0, 5} 0, 5 = 3$

Bài 2 trang 68 SGK Giải tích 12: Tính:

a) $4^{\log_{2} 3}$ ;

27^{\log_{9} 2}

;

9^{\log_{\sqrt{3}} 2}

4^{\log_{8} 27}

;

Phương pháp giải:

+) Công thức lũy thừa: ${(a^{m})}^{n} = a^{m . n}; \sqrt{a^{m}} = a^{\frac{m}{2}} .$

+) Sử dụng công thức logarit: $a^{\log_{a} b} = b; \log_{a} b^{n} = n \log_{a} b;$ $\log_{a^{m}} b = \frac{1}{m} \log_{a} b .$

Lời giải:

$4^{\log_{2} 3} = {(2^{2})}^{\log_{2} 3} = {(2^{\log_{2} 3})}^{2} = 3^{2} = 9$ .

$27^{\log_{9} 2} = {(3^{3})}^{\log_{9} 2} = 3^{3. \log_{9} 2} = 3^{3 \log_{3^{2}} 2}$ $= 3^{3. \frac{1}{2} \log_{3} 2} = 3^{\frac{3}{2} . \log_{3} 2}$ $= {(3^{\log_{3} 2})}^{\frac{3}{2}} = 2^{\frac{3}{2}} = {(\sqrt{2})}^{3} = 2 \sqrt{2}$

$9^{\log_{\sqrt{3}} 2} = {({(\sqrt{3})}^{4})}^{l o g_{\sqrt{3}} 2}$ $= {(\sqrt{3})}^{4 \log_{\sqrt{3}} 2}$ $= {({(\sqrt{3})}^{l o g_{\sqrt{3}} 2})}^{4} = 2^{4}$ $= 16$

Cách khác:

$9^{\log_{\sqrt{3}} 2} = 9^{\log_{3^{1 / 2}} 2} = 9^{\frac{1}{1 / 2} \log_{3} 2}$ $= 9^{2 \log_{3} 2} = {(3^{2})}^{2 \log_{3} 2} = 3^{4 \log_{3} 2}$ $= {(3^{\log_{3} 2})}^{4} = 2^{4} = 16$

Có:

$l o g_{8} 27 = \log_{2^{3}} 3^{3}$ $= \frac{3}{3} . \log_{2} 3 = l o g_{2} 3$

Vậy $4^{\log_{8} 27} = {(2^{2})}^{\log_{2} 3} = {(2^{\log_{2} 3})}^{2}$ $= 3^{2} = 9$ .

Bài 3 trang 68 SGK Giải tích 12: Rút gọn biểu thức:

a) $\log_{3} 6. \log_{8} 9. \log_{6} 2$ ;

\log_{a} b^{2} + \log_{a^{2}} b^{4}

Phương pháp giải:

+) Sử dụng công thức logarit: $\log_{a} b . \log_{b} c = \log_{a} c; \log_{a} b^{n} = n . \log_{a} b; \log_{a^{m}} b = \frac{1}{m} . \log_{a} b; \log_{a^{m}} b^{n} = \frac{n}{m} . \log_{a} b .$

Với điều kiện các biểu thức đều có nghĩa.

Lời giải:

$\begin{array}{l} \log_{3} 6. \log_{8} 9. \log_{6} 2 \\ = (\log_{3} 6. \log_{6} 2) . \log_{8} 9 \\ = \log_{3} 2. \log_{2^{3}} 3^{2} \\ = \log_{3} 2. (2. \frac{1}{3} . \log_{2} 3) \\ = \frac{2}{3} . (\log_{3} 2. \log_{2} 3) \\ = \frac{2}{3} . \log_{3} 3 \\ = \frac{2}{3} \end{array}$

$\log_{a} b^{2} + \log_{a^{2}} b^{4}$

$= \log_{a} b^{2} + \log_{a^{2}} {(b^{2})}^{2}$

$= \log_{a} b^{2} + 2. \frac{1}{2} . \log_{a} b^{2}$

$= \log_{a} b^{2} + \log_{a} b^{2}$

$= 2 \log_{a} b^{2}$

$= 4 \log_{a} | b |$

Cách khác:

$\begin{array}{l} \log_{a} b^{2} + \log_{a^{2}} b^{4} \\ = 2 \log_{a} | b | + 4. \frac{1}{2} . \log_{a} | b | \\ = 2 \log_{a} | b | + 2. \log_{a} | b | \\ = 4 \log_{a} | b | \end{array}$

Bài 4 trang 68 SGK Giải tích 12: So sánh các cặp số sau:

a) $\log_{3} 5$ và $\log_{7} 4$ ;

\log_{0, 3} 2

và

\log_{5} 3

;

\log_{2} 10

và

\log_{5} 30

Phương pháp giải:

a) Sử dụng so sánh bắc cầu, so sánh với $1$

b) Sử dụng so sánh bắc cầu, so sánh với $0$

c) Sử dụng so sánh bắc cầu, so sánh với $3$

Lời giải:

$\begin{array}{l} Đặt \log_{3} 5 = α; \log_{7} 4 = β . \\ 3^{α} = 3^{\log_{3} 5} = 5 > 3^{1} \Rightarrow α > 1 (Vì 3 > 1) . \\ 7^{β} = 7^{\log_{7} 4} = 4 < 7^{1} \Rightarrow β < 1 (Vì 7 > 1) . \\ Do đó α > β . \end{array}$

Cách khác:

Ta có: $\log_{3} 5 > \log_{3} 3 = 1;$ $\log_{7} 4 < \log_{7} 7 = 1$ .

Do đó $\log_{3} 5 > 1 > \log_{7} 4$ hay $\log_{3} 5 > \log_{7} 4$ .

$\begin{array}{l} Đặt \log_{0, 3} 2 = α; \log_{5} 3 = β . \\ 0, 3^{α} = 0, 3^{\log_{0, 3} 2} = 2 > 0, 3^{0} \Rightarrow α < 0 (Vì 0 < 0, 3 < 1) . \\ 5^{β} = 5^{\log_{5} 3} = 3 > 3^{0} \Rightarrow β > 0 (Vì 3 > 1) . \\ Do đó α < β . \end{array}$

Cách khác:

Ta có: $\log_{0, 3} 2 < \log_{0, 3} 1 = 0$ (vì $0 < 0, 3 < 1$ ).

Lại có $\log_{5} 3 > \log_{5} 1 = 0$ (vì $5 > 1$ ).

Do đó $\log_{0, 3} 2 < 0 < \log_{5} 3$ hay $\log_{0, 3} 2 < \log_{5} 3$ .

$\begin{array}{l} Đặt \log_{2} 10 = α; \log_{5} 30 = β . \\ 2^{α} = 2^{\log_{2} 10} = 10 > 2^{3} \Rightarrow α > 3 (Vì 2 > 1) . \\ 5^{β} = 5^{\log_{5} 30} = 30 < 5^{3} \Rightarrow β < 3 (Vì 5 > 1) . \\ Do đó α > β . \end{array}$

Cách khác:

Ta có: $\log_{2} 10 > \log_{2} 8 = \log_{2} (2^{3}) = 3$

Lại có $\log_{5} 30 < \log_{5} 125 = \log_{5} (5^{3}) = 3$ .

Do đó $\log_{2} 10 > 3 > \log_{3} 50$ hay $\log_{2} 10 > \log_{3} 50$ .

Bài 5 trang 68 SGK Giải tích 12: a) Cho

a = \log_{30} 3, b = \log_{30} 5

. Hãy tính

\log_{30} 1350

theo

a, b

b) Cho

c = \log_{15} 3

. Hãy tính

\log_{25} 15

theo

c

Phương pháp giải:

+) Biến đổi các biểu thức logarit cần tính thông qua các logarit đề bài đã cho nhờ các công thức biến đổi cơ bản của logarit.

+) Thế các giá trị a, b vào biểu thức vừa biến đổi được ta tính được giá trị của biểu thức logarit cần tính.

Lời giải:

Ta có $1350 = {30.3}^{2} .5$ suy ra

$\log_{30} 1350 = \log_{30} (30. 3^{2} .5) = \log_{30} 30 + \log_{30} 3^{2} + \log_{30} 5 = 1 + 2 \log_{30} 3 + \log_{30} 5 = 1 + 2 a + b .$

Ta có: $\log_{25} 15 = \frac{1}{\log_{15} 25} = \frac{1}{\log_{15} 5^{2}} = \frac{1}{2 \log_{15} 5} = \frac{1}{2 \log_{15} (15 : 3)}$ $= \frac{1}{2 (\log_{15} 15 - l o g_{15} 3)} = \frac{1}{2 (1 - \log_{15} 3)} = \frac{1}{2 (1 - c)}$

Cách khác:

$\begin{array}{l} \log_{25} 15 = \log_{5^{2}} 15 = \frac{1}{2} \log_{5} 15 \\ = \frac{1}{2} \log_{5} (5.3) = \frac{1}{2} (\log_{5} 5 + \log_{5} 3) \\ = \frac{1}{2} (1 + \log_{5} 3) (1) \\ c = \log_{15} 3 \\ \Rightarrow \frac{1}{c} = \log_{3} 15 = \log_{3} (3.5) \\ = \log_{3} 3 + \log_{3} 5 = 1 + \log_{3} 5 \\ \Rightarrow \log_{3} 5 = \frac{1}{c} - 1 = \frac{1 - c}{c} \\ \Rightarrow \frac{1}{\log_{3} 5} = \frac{c}{1 - c} \\ \Rightarrow \log_{5} 3 = \frac{c}{1 - c} (2) \end{array}$

Thay (2) vào (1) ta được:

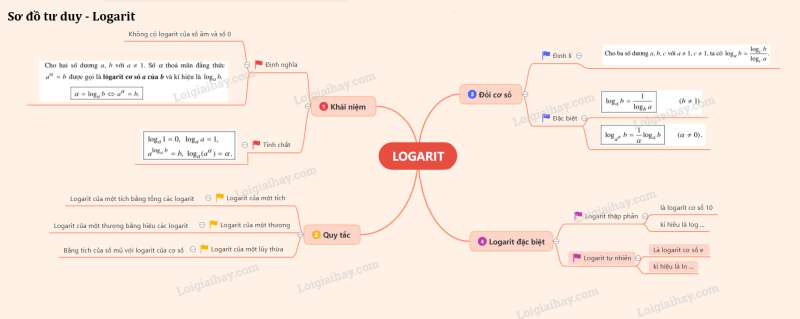
$\begin{array}{l} \log_{25} 15 = \frac{1}{2} (1 + \log_{5} 3) \\ = \frac{1}{2} (1 + \frac{c}{1 - c}) = \frac{1}{2} . \frac{1 - c + c}{1 - c} \\ = \frac{1}{2 (1 - c)} \end{array}$

Lý thuyết Bài 3: Lôgarit

1. Định nghĩa

Cho hai số dương a, b với $a \neq 1$ . Nghiệm duy nhất của phương trình $a^{x} = b$ được gọi là $\log_{a} b$ ( tức là số $α$ có tính chất là $a^{α} = b$ ).

Như vậy $\log_{a} b = α \Leftrightarrow a^{α} = b$ .

Ví dụ: $\log_{4} 16 = 2$ vì $4^{2} = 16$ .

2. Lôgarit thập phân và lôgarit tự nhiên

Lôgarit cơ số 10 còn được gọi là lôgarit thập phân, số log10b thường được viết là logb hoặc lgb.

Lôgarit cơ số $e$ ( $e = lim_{n \to + \infty} {(1 + \frac{1}{n})}^{n}$ ≈ 2,718281828459045) còn được gọi là lôgarit tự nhiên, số logeb thường được viết là lnb.

3. Tính chất của lôgarit

Lôgarit có các tính chất rất phong phú, có thể chia ra thành các nhóm sau đây:

1) Lôgarit của đơn vị và lôgarit của cơ số:

Với cơ số tùy ý, ta luôn có loga1 = 0 và logaa= 1.

2) Phép mũ hóa và phép lôgarit hóa theo cùng cơ số (mũ hóa số thực α theo cơ số a là tính aα; lôgarit hóa số dương b theo cơ số a là tính logab) là hai phép toán ngược nhau.

$\forall a > 0 (a \neq$ 1), $\forall b > 0$ , $a^{\log_{a} b} = b$

$\forall a > 0 (a \neq 1)$ , $\log_{a} a^{α} = α$

3) Lôgarit và các phép toán: Phép lôgarit hóa biến phép nhân thành phép cộng, phép chia thành phép trừ, phép nâng lên lũy thừa thành phép nhân, phép khai căn thành phép chia, cụ thể là

Với $\forall a, b_{1}, b_{2} > 0, a \neq 1$ ta có:

+) $\log_{a} (b_{1} b_{2}) = \log_{a} b_{1} + \log_{a} b_{2}$

+) $\log_{a} (\frac{b_{1}}{b_{2}}) = \log_{a} b_{1} - \log_{a} b_{2}$

+) $\forall a, b > 0 (a \neq 1),$ $\forall α$ ta có:

$\log_{a} b^{α} = α . \log_{a} b$

$\log_{a} \sqrt[n]{b} = \frac{1}{n} . \log_{a} b$

Ví dụ: Tính $A = \log_{2} \frac{15}{2} - 2 \log_{2} \sqrt{3}$ .

Ta có:

$\begin{array}{l} A = \log_{2} \frac{15}{2} - 2 \log_{2} \sqrt{3} \\ = \log_{2} 15 - \log_{2} 2 - 2. \frac{1}{2} \log_{2} 3 \\ = \log_{2} (3.5) - 1 - \log_{2} 3 \\ = \log_{2} 3 + \log_{2} 5 - 1 - \log_{2} 3 \\ = \log_{2} 5 - 1 \end{array}$

4) Đổi cơ số: Có thể chuyển các phép lấy lôgarit theo những cơ số khác nhau về việc tính lôgarit theo cùng một cơ số chung, cụ thể là

$\forall a, b, c > 0 (a, c \neq 1)$ , $\log_{a} b = \frac{\log_{c} b}{\log_{c} a}$ .

Đặc biệt $\forall a, b > 0 (a, b \neq 1) \log_{a} b = \frac{1}{\log_{b} a}$

$\forall a, b > 0 (a \neq 1), \forall α, β (α \neq 0)$ ta có:

$\log_{a^{α}} b = \frac{1}{α} \log_{a} b$

$\log_{a^{α}} b^{β} = \frac{β}{α} \log_{a} b$

$\log_{a} \frac{1}{b} = - \log_{a} b (0 < a \neq 1; b > 0)$

$\log_{a} \sqrt[n]{b} = \log_{a} b^{\frac{1}{n}} = \frac{1}{n} \log_{a} b$ $(0 < a \neq 1; b > 0; n > 0; n \in N^{*})$

$\log_{a} b . \log_{b} c = \log_{a} c \Leftrightarrow \log_{b} c = \frac{\log_{a} c}{\log_{a} b}$ $(0 < a, b \neq 1; c > 0)$

$\log_{a} b = \frac{1}{\log_{b} a} \Leftrightarrow \log_{a} b . \log_{b} a = 1$ $(0 < a, b \neq 1)$

$\log_{a^{n}} b = \frac{1}{n} \log_{a} b$ $(0 < a \neq 1; b > 0; n \neq 0)$

Ví dụ: Tính $B = 3 \log_{8} 12 - 2 \log_{2} 3 + 12 \log_{16} \sqrt[3]{3}$

Ta có:

$\begin{array}{l} B = 3 \log_{8} 12 - 2 \log_{2} 3 + 12 \log_{16} \sqrt[3]{3} \\ = 3 \log_{2^{3}} 12 - 2 \log_{2} 3 + 12. \log_{2^{4}} \sqrt[3]{3} \\ = 3. \frac{1}{3} \log_{2} 12 - 2 \log_{2} 3 + 12. \frac{1}{4} \log_{2} \sqrt[3]{3} \\ = \log_{2} 12 - 2 \log_{2} 3 + 3 \log_{2} \sqrt[3]{3} \\ = \log_{2} 12 - \log_{2} 3^{2} + \log_{2} {(\sqrt[3]{3})}^{3} \\ = \log_{2} 12 - \log_{2} 9 + \log_{2} 3 \\ = \log_{2} \frac{12.3}{9} \\ = \log_{2} 4 \\ = \log_{2} 2^{2} \\ = 2 \end{array}$

Hệ quả:

a) Nếu $a > 1; b > 0$ thì $\log_{a} b > 0 \Leftrightarrow b > 1;$ $\log_{a} b < 0 \Leftrightarrow 0 < b < 1$ .

b) Nếu $0 < a < 1; b > 0$ thì $\log_{a} b < 0 \Leftrightarrow b > 1;$ $\log_{a} b > 0 \Leftrightarrow 0 < b < 1$ .

c) Nếu $0 < a \neq 1; b, c > 0$ thì $\log_{a} b = \log_{a} c \Leftrightarrow b = c$ .

Chú ý:

Logarit thập phân

\log_{10} b = \log b (= \lg b)

có đầy đủ tính chất của logarit cơ số

a

Sơ đồ tư duy về lôgarit

Các dạng toán thường gặp về logarit

Dạng 1: Tính giá trị biểu thức, rút gọn biểu thức logarit.

Phương pháp:

- Bước 1: Biến đổi các biểu thức có chứa logarit sử dụng những tính chất của logarit.

- Bước 2: Thực hiện tính toán dựa vào thứ tự thực hiện phép tính:

+ Nếu không có ngoặc: Lũy thừa (căn bậc $n$ ) $\to$ nhân, chia $\to$ cộng, trừ.

+ Nếu có ngoặc: Thực hiện trong ngoặc $\to$ lũy thừa (căn bậc $n$ ) $\to$ nhân, chia $\to$ cộng, trừ.

Dạng 2: So sánh các biểu thức có chứa logarit.

Phương pháp:

- Bước 1: Đưa các logarit về cùng cơ số (nếu có thể)

- Bước 2: Đơn giản các biểu thức đã cho bằng cách sử dụng tính chất của logarit.

- Bước 3: So sánh các biểu thức sau khi đơn giản, sử dụng một số tính chất của so sánh logarit.

Dạng 3: Biểu diễn một logarit hoặc rút gọn biểu thức có chứa logarit qua các logarit đã cho.

Phương pháp:

- Bước 1: Tách biểu thức cần biểu diễn ra để xuất hiện các logarit đề bài cho bằng cách sử dụng các tính chất của logarit.

- Bước 2: Thay các giá trị bài cho vào và rút gọn sử dụng thứ tự thực hiện phép tính:

+ Nếu không có ngoặc: Lũy thừa (căn bậc $n$ ) $\to$ nhân, chia $\to$ cộng, trừ.

+ Nếu có ngoặc: Thực hiện trong ngoặc $\to$ lũy thừa (căn bậc $n$ ) $\to$ nhân, chia $\to$ cộng, trừ.

Logarit (số e và logarit tự nhiên)

1. Các kiến thức cần nhớ

a) Logarit tự nhiên

Định nghĩa:

Logarit cơ số $e$ của 1 số dương $a$ được gọi là logarit tự nhiên (logarit Nê-pe) của số $a$ và kí hiệu là $\ln a$ .

$\ln a = b \Leftrightarrow a = e^{b} (a > 0); e \approx 2, 71828...$

Tính chất:

Lôgarit tự nhiên có đầy đủ tính chất của logarit với cơ số lớn hơn 1.

b) Công thức lãi kép liên tục (hoặc công thức tăng trưởng mũ)

$T = A . e^{N r}$ , ở đó $A$ là số tiền gửi ban đầu, $r$ là lãi suất, $N$ là số kì hạn.

2. Một số dạng toán thường gặp

Dạng 1: Tính giá trị biểu thức, rút gọn biểu thức logarit tự nhiên.

Phương pháp:

- Bước 1: Biến đổi các biểu thức có chứa $\ln$ sử dụng những tính chất của logarit tự nhiên.

- Bước 2: Thực hiện tính toán dựa vào thứ tự thực hiện phép tính:

+ Nếu không có ngoặc: Lũy thừa (căn bậc $n$ ) $\to$ nhân, chia $\to$ cộng, trừ.

+ Nếu có ngoặc: Thực hiện trong ngoặc $\to$ lũy thừa (căn bậc $n$ ) $\to$ nhân, chia $\to$ cộng, trừ.

Dạng 2: So sánh các biểu thức có chứa logarit tự nhiên.

Phương pháp:

- Bước 1: Đơn giản các biểu thức đã cho bằng cách sử dụng tính chất của logarit và logarit tự nhiên.

- Bước 2: So sánh các biểu thức sau khi đơn giản, sử dụng một số tính chất của so sánh logarit.

Dạng 3: Biểu diễn một logarit hoặc rút gọn biểu thức có chứa logarit qua các logarit đã cho.

Phương pháp:

- Bước 1: Tách biểu thức cần biểu diễn ra để xuất hiện các logarit đề bài cho bằng cách sử dụng các tính chất của logarit.

- Bước 2: Thay các giá trị bài cho vào và rút gọn sử dụng thứ tự thực hiện phép tính:

+ Nếu không có ngoặc: Lũy thừa (căn bậc $n$ ) $\to$ nhân, chia $\to$ cộng, trừ.

+ Nếu có ngoặc: Thực hiện trong ngoặc $\to$ lũy thừa (căn bậc $n$ ) $\to$ nhân, chia $\to$ cộng, trừ.

Dạng 4: Bài toán lãi kép liên tục.

Một người gửi vào ngân hàng số tiền $A$ đồng, lãi suất $r$ theo năm, tính số tiền có được sau $N$ năm.

Phương pháp:

Sử dụng công thức tăng trưởng mũ:

$T = A . e^{N r}$ , ở đó $A$ là số tiền gửi ban đầu, $r$ là lãi suất, $N$ là số kì hạn.

Bài giảng Toán học 12 Bài 3: Lôgarit

Xem thêm các chương trình khác:

Bài trước

Bài sau

Giải SGK, SBT, Chuyên đề Toán Học Lớp 12

Giải Toán 12 Bài 3: Lôgarit

Xem thêm các chương trình khác: