Chúng tôi giới thiệu Giải bài tập Toán lớp 12 Bài 3: Khái niệm về thể tích của khối đa diện chính xác, chi tiết nhất giúp học sinh dễ dàng làm bài tập Khái niệm về thể tích của khối đa diện lớp 12.
Bài giảng Toán 12: Thể tích khối đa diện có cạnh bên vuông góc với mặt đáy
Giải bài tập Toán lớp 12 Bài 3: Khái niệm về thể tích của khối đa diện
Trả lời câu hỏi giữa bài
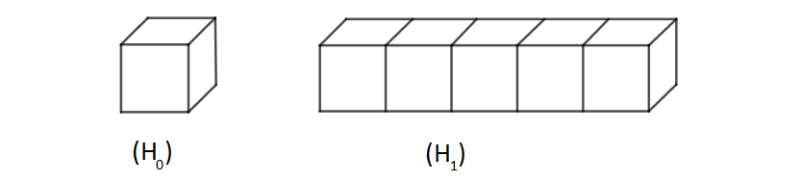
Lời giải:
Hình được tạo bởi 5 khối lập phương .
Nói cách khác, có thể chia thành 5 khối lập phương
Trả lời câu hỏi 2 trang 22 SGK Hình học 12: Có thể chia (H2) thành bao nhiêu khối hộp chữ nhật bằng (H1)?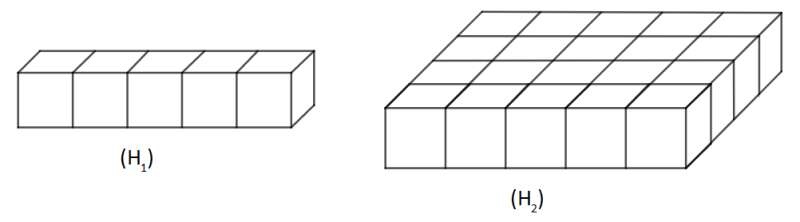
Lời giải:
Có thể chia (H2) thành 4 khối hộp chữ nhật (H1)
Trả lời câu hỏi 3 trang 22 SGK Hình học 12: Có thể chia (H) thành bao nhiêu khối hộp chữ nhật bằng (H2) ?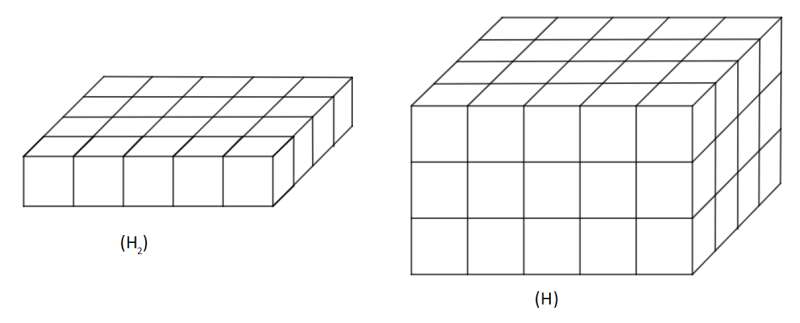
Lời giải:
Có thể chia (H) thành 3 khối hộp chữ nhật (H2)

Phương pháp giải:
Công thức tính thể tích khối chóp: trong đó lần lượt là diện tích đáy và chiều cao của khối chóp.
Lời giải:
Kim tự tháp là khối chóp tứ giác đều nên đáy là hình vuông có cạnh 230m
Diện tích đáy là:
Thể tích kim tự tháp là:
Phương pháp giải:
+) Gọi là đường cao hạ từ đỉnh của tứ diện đều .
+) Do tứ diện đều, chứng minh là trọng tâm tam giác .
+) Sử dụng định lí Pytago tính độ dài .
+) Áp dụng công thức tính thể tích: .
Lời giải:
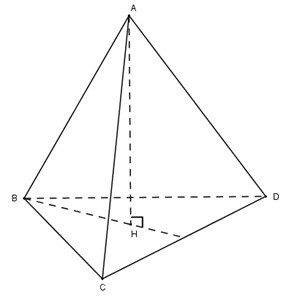
Cho tứ diện đều . Hạ
Dễ dàng chứng minh được do đó H là tâm đường tròn ngoại tiếp tam giác .
Do là tam giác đều nên là trọng tâm của tam giác .
Gọi là trung điểm thì vừa là trung tuyến vừa là đường cao trong tam giác.
Ta có:
Do đó
Áp dụng định lí Pitago trong tam giác vuông ta có:
Do tam giác đều cạnh nên:
Vậy
Phương pháp giải:
+) Chia khối bát diện đều thành hai khối chóp tứ giác đều.
+) Xác định chiều cao và áp dụng công thức tính thể tích khối chóp:
Lời giải:

Chia khối tám mặt đều cạnh thành hai khối chóp tứ giác đều cạnh là và .
Xét chóp tứ giác đều . Gọi là tâm hình vuông ta có: .
Vì là hình vuông cạnh nên
.
Áp dụng định lí Pitago trong tam giác vuông có:
Vậy thể tích khối tám mặt đều cạnh là: .
Chú ý: Hình chóp đa giác đều có hình chiếu của đỉnh trên mặt đáy trùng với tâm mặt đáy.
Phương pháp giải:
+) Gọi là diện tích đáy và là chiều cao của khối hộp. Tính thể tích của khối hộp.
+) Chia khối hộp thành khối tứ diện và bốn khối chóp và . Tính thể tích của bốn khối chóp và .
+) Suy ra
+) Tính tỉ số thể tích.
Lời giải:
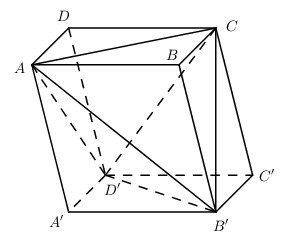
Gọi là diện tích đáy và là chiều cao của khối hộp thì thể tích của khối hộp:
Chia khối hộp thành khối tứ diện và bốn khối chóp và .
Xét khối chóp có diện tích đáy và chiều cao bằng . Do đó .
Tương tự như vậy ta chứng minh được:
Vậy
.
Phương pháp giải:
+) Gọi và lần lượt là chiều cao hạ từ và đến , dựa vào định lí Vi-et tính tỉ số .
+) Sử dụng công thức tính diện tích tính diện tích tam giác , tương tự tính diện tích tam giác , sau đó suy ra tỉ số .
+) Sử dụng công thức tính thể tích lập tỉ số thể tích và , rút gọn và suy ra kết quả.
Lời giải:
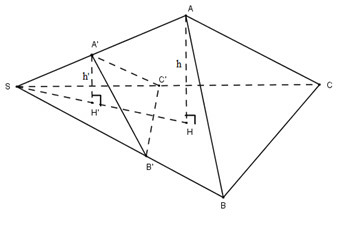
Gọi và lần lượt là chiều cao hạ từ đến mặt phẳng .
* Do nên bốn điểm và đồng phẳng. (1)
Lại có, 3 điểm đồng phẳng (2).
Từ (1) và (2) suy ra, 5 điểm và đồng phẳng.
Trong mp(ASH) ta có:
⇒ Ba điểm và thẳng hàng.
Gọi và theo thứ tự là diện tích các tam giác và .
Khi đó ta có (định lý Ta - let) và:
Suy ra
Đó là điều phải chứng minh.
Chú ý: Từ nay về sau chúng ta được sử dụng bài tập này như một kết quả và không cần chứng minh lại.
Bài 5 trang 26 SGK Hình học 12: Cho tam giác vuông cân ở và . Trên đường thẳng qua và vuông góc với mặt phẳng lấy điểm sao cho . Mặt phẳng qua vuông góc với , cắt tại và cắt tại . Tính thể tích khối tứ diện theo .Phương pháp giải:
Bước 1: Dựng các điểm và
Bước 2: Tìm chiều cao và đáy tương ứng:
Bước 3: Chứng minh tam giác vuông tại
Suy ra
Lời giải:

Ta có: hay do đó ta đã biết chiều cao của tứ diện
Để tính thể tích tứ diện này, ta đi tính diện tích đáy tương ứng là
Dễ thấy: vuông tại vì:
Vậy ta đi tính các cạnh
+) Tính
Do nên vuông cân tại
Chiều cao
+) Tính :
Xét vuông tại , ta có:
Vậy
+) Chiều cao
Vậy
Lời giải:
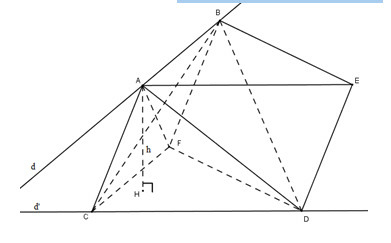
Gọi là độ dài đường vuông góc chung của và , là góc giữa hai đường thẳng và . Qua dựng hình bình hành . Qua dựng hình bình hành .
Khi đó là một hình lăng trụ tam giác. Ta có:
Kẻ ta có:
Ta có:
Vậy . (đpcm)
1. Khái niệm về thể tích khối đa diện
Có thể đặt tương ứng cho mỗi khối đa diện một số dương thỏa mãn các tính chất sau:
a) Nếu là khối lập phương có cạnh bằng một thì
b) Nếu hai khối đa diện và bằng nhau thì
=
c) Nếu khối đa diện được phân chia thành hai khối đa diện và thì
Số dương nói trên được gọi là thể tích của khối đa diện .
Khối lập phương có cạnh bằng một được gọi là khối lập phương đơn vị.
Nếu là khối lăng trụ chẳng hạn thì thể tích của nó còn được kí hiệu là
2. Thể tích khối lăng trụ
Thể tích của khối lăng trụ có diện tích đáy bằng và chiều cao bằng là
Đặc biệt thể tích của khối hộp chữ nhật bằng tích của ba kích thước của nó.
3. Thể tích khối chóp
Thể tích của khối chóp có diện tích đáy bằng và chiều cao bằng là
Kiến thức bổ sung
4. Cho hình chóp . Trên ba tia lần lượt lấy ba điểm .
Khi đó
5. Nếu là ảnh của qua một phép dời hình thì
=
Nếu là ảnh của qua một phép vị tự tỉ số thì
= .
Sơ đồ tu duy về thể tích khối đa diện
Bài giảng Toán 12: Thể tích khối đa diện có hình chiếu là điểm đặc biệt trên đáy

