Giải Toán 12 Bài 1: Lũy thừa

Lời giải:

$\begin{array}{l}{\left(1,5\right)}^4=5,0625\\ {\left({\displaystyle \frac{-2}{3}}\right)}^3={\displaystyle \frac{-8}{27}}\\ {\left(\sqrt{3}\right)}^5=9\sqrt{3}\end{array}$

Lời giải:

Ta có: Số nghiệm của phương trình $x^3=b$  là số giao điểm của hai đồ thị hàm số $y=x^3$ và $y=b$ .

Dựa vào H26 ta thấy: với mọi b: đồ thị hàm số  $y=x^3$ luôn cắt đường thẳng  $y=b$ tại một điểm duy nhất do đó phương trình $x^3=b$ có nghiệm duy nhất với mọi b.

Số nghiệm của phương trình $x^4=b$ (1) là số giao điểm của hai đồ thị hàm số  $y=b$ và  $y=x^4$ . Dựa và hình 27 ta thấy:

+ Với $b<0$ hai đồ thị hàm số trên không giao nhau, vậy phương trình (1) vô nghiệm.

+ Với $b=0$, hai đồ thị hàm số tiếp xúc nhau tại $(0,0)$, vậy phương trình (1) có nghiệm duy nhất $x=0.$

+ Với $b>0$, hai đồ thị hàm số cắt nhau tại hai điểm phân biết, vậy phương trình (1) có hai nghiệm phân biệt.

Lời giải:

Đặt $\sqrt[n]{a}=x;\sqrt[n]{b}=y$.

Theo định nghĩa về căn bậc $n$ ta có:  $x^n=a;y^n=b$

$a.b=x^n.y^n=(xy{)}^n$ 

Vậy $xy$ là căn bậc $n$ của ab.

Hay $\sqrt[n]{ab}=xy=\sqrt[n]{a}.\sqrt[n]{b}$

Lời giải:

Với $m,n\in N^{\ast }$ ta có các tính chất sau đây:

a. Các tính chất về đẳng thức

$$\begin{gathered} 1.a^m.a^n=a^{m+n} \\ 2.a^m:a^n=a^{m-n}(m\ge n) \\ 3.{\left(a^m\right)}^n=a^{m.n} \\ 4.{\left(\frac{a}{b}\right)}^m=\frac{a^m}{b^m}(b\ne 0) \\ 5.(ab{)}^m=a^m.b^n \end{gathered}$$

b. Các tính chất về bất đẳng thức

Với $a>1$ thì $a^m>a^n\iff m>n$.

Với $0<a<1$ thì $a^m>a^n\iff m<n$.

Với $0<a<b$ thì $a^m>b^m$

Lời giải:

$\begin{array}{l}{\displaystyle \frac{{(a^{\sqrt{3}-1})}^{\sqrt{3}+1}}{a^{\sqrt{5}-3}.a^{4-\sqrt{5}}}}={\displaystyle \frac{a^{\left(\sqrt{3}-1\right)\left(\sqrt{3}+1\right)}}{a^{\left(\sqrt{5}-3\right)+\left(4-\sqrt{5}\right)}}}\\ ={\displaystyle \frac{a^{3-1}}{a^1}}={\displaystyle \frac{a^2}{a}}=a.\end{array}$

Lời giải:

Ta có:

$\{\begin{array}{c}0<{\displaystyle \frac{3}{4}}<1\hfill \\ \sqrt{8}<\sqrt{9}=3\hfill \end{array}\Rightarrow {\left({\displaystyle \frac{3}{4}}\right)}^{\sqrt{8}}>{\left({\displaystyle \frac{3}{4}}\right)}^3$

I. KHÁI NIỆM LŨY THỪA

1. Lũy thừa với số mũ nguyên

Định nghĩa

Cho $n$ là một số nguyên dương.

Với $a$ là một số thực tùy ý, lũy thừa bậc $n$ của $a$ là tích của $n$ thừa số $a$.

$a^n=a.a.a.....a$ ($n$ thừa số $a$)

Với $a\ne 0$ thì $a^0=1,a^{-n}={\displaystyle \frac{1}{a^n}}$.

Chú ý

$0^n$ và $0^{-n}$ không có nghĩa.

Lũy thừa với số mũ nguyên có các tính chất tương tự của lũy thừa với số mũ nguyên dương.

2. Căn bậc $n$

a) Định nghĩa

Cho số thực $b$ và số nguyên dương $n\left(n\ge 2\right)$. Số $a$ được gọi là căn bậc $n$ của số $b$ nếu $a^n=b$.

b) Chú ý

+) Với $n$ lẻ và $b\in \mathbb{R}$ thì có duy nhất một căn bậc $n$ của $b$, kí hiệu $\sqrt[n]{b}$.

+) Với $n$ chẵn và:

$b<0$ thì không tồn tại căn bậc $n$ của $b$.

$b=0$ thì có duy nhất một căn bậc $n$ của $b$ là số $0$.

$b>0$ thì có hai căn trái dấu, kí hiệu $\sqrt[n]{b}$ và $-\sqrt[n]{b}$.

c) Tính chất

$\begin{array}{l}\sqrt[n]{a}.\sqrt[n]{b}=\sqrt[n]{ab}\\ {\displaystyle \frac{\sqrt[n]{a}}{\sqrt[n]{b}}}=\sqrt[n]{{\displaystyle \frac{a}{b}}}\\ {\left(\sqrt[n]{a}\right)}^m=\sqrt[n]{a^m}\\ \sqrt[n]{a^n}=\{\begin{array}{l}a,\text{nếu}n\text{lẻ}\\ \left|a\right|,\text{nếu}n\text{chẵn}\end{array}\\ \sqrt[n]{\sqrt[k]{a}}=\sqrt[nk]{a}\end{array}$

Ví dụ

$\sqrt[3]{-4}.\sqrt[3]{54}=\sqrt[3]{\left(-4\right).54}=\sqrt[3]{-216}=-6$

3. Lũy thừa với số mũ hữu tỉ

Cho số thực $a$ dương và số hữu tỉ $r={\displaystyle \frac{m}{n}}$, trong đó $m\in \mathbb{Z}$, $n\in \mathbb{N}$, $n\ge 2$.

Lũy thừa của số $a$ với số mũ $r$ là số $a^r$ xác định bởi

$a^r=a^{\frac{m}{n}}=\sqrt[n]{a^m}$

Đặc biệt:  Khi $m=1$: $a^{\frac{1}{n}}=\sqrt[n]{a}$

Ví dụ:

${16}^{-\frac{3}{4}}=\sqrt[4]{{16}^{-3}}={\displaystyle \frac{1}{\sqrt[4]{{16}^3}}}$ $={\displaystyle \frac{1}{{\left(\sqrt[4]{16}\right)}^3}}={\displaystyle \frac{1}{2^3}}={\displaystyle \frac{1}{8}}$

II. TÍNH CHẤT CỦA LŨY THỪA VỚI SỐ MŨ THỰC

Cho $a,b$ là những số thực dương; $\alpha ,\beta$ là những số thực tùy ý. Khi đó ta có:

$\begin{array}{l}{a}^{\alpha }.a^{\beta }=a^{\alpha +\beta }\\ {\displaystyle \frac{a^{\alpha }}{a^{\beta }}}=a^{\alpha -\beta }\\ {\left(a^{\alpha }\right)}^{\beta }=a^{\alpha \beta }\\ {\left(ab\right)}^{\alpha }=a^{\alpha }{b}^{\alpha }\\ {\left({\displaystyle \frac{a}{b}}\right)}^{\alpha }={\displaystyle \frac{a^{\alpha }}{b^{\alpha }}}\end{array}$

Nếu $a>1$ thì $a^{\alpha }>a^{\beta }\iff \alpha >\beta$.

Nếu $a<1$ thì $a^{\alpha }>a^{\beta }\iff \alpha <\beta$.

Ví dụ: Rút gọn biểu thức: $A={\displaystyle \frac{a^{\sqrt{2}+1}.a^{3-\sqrt{2}}}{{\left(a^{\sqrt{3}-1}\right)}^{\sqrt{3}+1}}}$

Ta có:

$\begin{array}{l}A={\displaystyle \frac{a^{\sqrt{2}+1}.a^{3-\sqrt{2}}}{{\left(a^{\sqrt{3}-1}\right)}^{\sqrt{3}+1}}}={\displaystyle \frac{a^{\sqrt{2}+1+3-\sqrt{2}}}{a^{\left(\sqrt{3}-1\right)\left(\sqrt{3}+1\right)}}}\\ ={\displaystyle \frac{a^4}{a^{3-1}}}=a^2\end{array}$

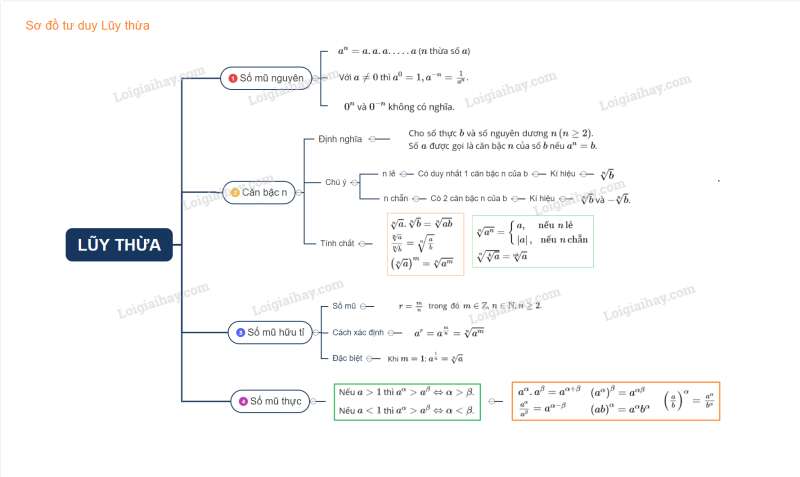
Sơ đồ tư duy về lũy thừa

Phương pháp:

- Bước 1: Đưa các lũy thừa về cùng cơ số hoặc số mũ (nếu có thể)

- Bước 2: Biến đổi các lũy thừa, căn bậc $n$ sử dụng các tính chất của lũy thừa với số mũ nguyên, hữu tỉ.

- Bước 3: Thực hiện tính toán với chú ý về thứ tự thực hiện các phép tính:

+ Nếu không có ngoặc: Lũy thừa (căn bậc $n$) $\to$ nhân, chia $\to$ cộng, trừ.

+ Nếu có ngoặc: Thực hiện trong ngoặc $\to$ lũy thừa (căn bậc $n$) $\to$ nhân, chia $\to$ cộng, trừ.

Ví dụ 1: Rút gọn biểu thức: $P=x^{\frac{1}{3}}.\sqrt[6]{x}$

Ta có: $P=x^{\frac{1}{3}}.\sqrt[6]{x}=x^{\frac{1}{3}}.x^{\frac{1}{6}}=x^{\frac{1}{3}+\frac{1}{6}}=x^{\frac{1}{2}}.$

Dạng 2: So sánh hai hay nhiều biểu thức.

Phương pháp:

- Bước 1: Đưa các lũy thừa về cùng cơ số hoặc số mũ(nếu có thể)

- Bước 2: Tính toán, rút gọn các biểu thức đã cho bằng cách sử dụng các tính chất của lũy thừa với số mũ hữu tỉ, căn bậc $n$.

- Bước 3: So sánh giá trị các biểu thức đã rút gọn dựa vào tính chất về so sánh hai lũy thừa:

1/ Với $a>1$ thì $a^m>a^n\iff m>n$

2/ Với $0<a<1$ thì $a^m>a^n\iff m<n$

3/ Với $0<a<b$ thì:

    a) $a^m<b^m\iff m>0$

    b) $a^m>b^m\iff m<0$

4/ Với $a>0,b>0$ thì $a^n=b^n\iff a=b$.

Ở đó $m,n$ là các số hữu tỉ.

5/ Với $a<b,n$ là số tự nhiên lẻ thì $a^n<b^n$

Ví dụ 2: Cho $a>1$, so sánh $\sqrt[15]{a^7}$ với $\sqrt[5]{a^2}$

Ta có: $\sqrt[15]{a^7}=a^{\frac{7}{15}};\sqrt[5]{a^2}=a^{\frac{2}{5}}$

Vì ${\displaystyle \frac{7}{15}}>{\displaystyle \frac{2}{5}}$ và $a>1$ nên $a^{\frac{7}{15}}>a^{\frac{2}{5}}$ hay $\sqrt[15]{a^7}>\sqrt[5]{a^2}$

2. Một số dạng toán thường gặp đối với lũy thừa với số mũ vô tỉ:

Dạng 1: Tính giá trị, rút gọn các biểu thức.

Phương pháp:

- Bước 1: Biến đổi các lũy thừa sử dụng các tính chất của lũy thừa với số mũ thực.

- Bước 2: Thực hiện tính toán với chú ý về thứ tự thực hiện các phép tính:

+ Nếu không có ngoặc: Lũy thừa (căn bậc $n$) $\to$ nhân, chia $\to$ cộng, trừ.

+ Nếu có ngoặc: Thực hiện trong ngoặc $\to$ lũy thừa (căn bậc $n$) $\to$ nhân, chia $\to$ cộng, trừ.

Dạng 2: So sánh hai hay nhiều biểu thức.

Phương pháp:

- Bước 1: Đưa các lũy thừa về cùng cơ số hoặc số mũ(nếu có thể)        

- Bước 2: Tính toán, rút gọn các biểu thức đã cho bằng cách sử dụng các tính chất của lũy thừa với số mũ hữu tỉ, số mũ thực, căn bậc $n$.

- Bước 3: So sánh giá trị các biểu thức đã rút gọn dựa vào tính chất về so sánh hai lũy thừa.