Chúng tôi giới thiệu Giải bài tập Toán lớp 12 Ôn tập chương III - Phương pháp toạ độ trong không gian chính xác, chi tiết nhất giúp học sinh dễ dàng làm bài tập Ôn tập chương III - Phương pháp toạ độ trong không gian lớp 12.
Giải bài tập Toán lớp 12 Ôn tập chương III - Phương pháp toạ độ trong không gian
a) Chứng minh là bốn đỉnh của một tứ diện.
b) Tìm góc giữa hai đường thẳng và .
c) Tính độ dài đường cao của hình chóp .
Phương pháp giải:
a) Chứng minh bốn điểm A, B, C, D là 4 đỉnh của 1 tứ diện tức là chứng minh 4 điểm này không đồng phẳng
Bằng cách viết phương trình mặt phẳng ( dạng đoạn chắn) rồi chứng minh .
b) Gọi là góc giữa hai đường thẳng ta có: .
c) Độ dài đường cao của hình chóp A.BCD bằng .
+) Viết phương trình mặt phẳng (BCD).
+) Áp dụng công thức tính khoảng cách từ điểm đến mặt phẳng là:
Lời giải:
a) Viết phương trình mặt phẳng : Theo phương trình mặt phẳng theo đoạn chắn, ta có:
:
Thế các toạ độ của vào vế phải của phương trình mặt phẳng , ta có:
Vậy hay bốn điểm không đồng phẳng, suy ra là bốn đỉnh của 1 tứ diện.
Cách khác:
không đồng phẳng.
không đồng phẳng
là 4 đỉnh của hình tứ diện
b) Gọi là góc giữa hai đường thẳng ta có:
Ta có: ,
c) Ta có
Gọi là vectơ pháp tuyến của thì:
Phương trình mặt phẳng :
Chiều cao của hình chóp bằng khoảng cách từ điểm đến mặt phẳng :
a) Tìm toạ độ tâm và tính bán kính của mặt cầu
b) Lập phương trình của mặt cầu .
c) Lập phương trình của mặt phẳng tiếp xúc với mặt cầu tại điểm .
Phương pháp giải:
a) Tâm I là trung điểm của AB: và bán kính .
b) Phương trình mặt cầu tâm và có bán kính có dạng:
c) Mặt phẳng cần tìm đi qua A và nhận là 1 VTPT.
Lời giải:
a) Tâm của mặt cầu là trung điểm của đoạn thẳng :
Vậy
b) Phương trình mặt cầu
c) Mặt phẳng tiếp xúc với mặt cầu tại điểm chính là mặt phẳng qua và vuông góc với bán kính . Ta có:
Phương trình mặt phẳng cần tìm là:
a) Viết phương trình mặt phẳng . Suy ra là một tứ diện.
b) Tính chiều cao của tứ diện
c) Viết phương trình mặt phẳng chứa và song song với .
Phương pháp giải:
a) Mặt phẳng đi qua và nhận là 1 VTPT. Chứng minh ABCD là tứ diện bằng cách chứng minh
b)
c) là 1 VTPT của mặt phẳng và đi qua A.
Lời giải:
a) Ta có: ,
Xét vectơ
Mặt phẳng đi qua và nhận làm vectơ pháp tuyến nên có phương trình:
Thay toạ độ của vào phương trình của ta có:
Điều này chứng tỏ điểm không thuộc mặt phẳng hay bốn điểm không đồng phẳng, và là một tứ diện.
b) Chiều cao của tứ diện chính là khoảng cách từ đến mặt phẳng :
=
c) Ta có: ,
Mặt phẳng chứa và chính là mặt phẳng đi qua và nhận cặp vectơ , làm cặp vectơ chỉ phương, có vectơ pháp tuyến
Ta có:
=
Vậy phương trình của là:
a) Đi qua hai điểm .
b) Đi qua điểm và song song với đường thẳng có phương trình
Phương pháp giải:
Phương trình tham số đường thẳng đi qua và nhận là 1 VTCP có dạng:
Lời giải:
a) Đường thẳng qua có vectơ chỉ phương nên phương trình tham số của có dạng:
b) Đường thẳng .
Mà là VTCP của nên là VTCP của d.
d đi qua M(2;3;-5) và nhận là VTCP nên phương trình tham số của đường thẳng là:
Hãy xác định toạ độ tâm và tính bán kính của đường tròn .
Phương pháp giải:
+) Xác định tâm I và bán kính R của mặt cầu (S).
+) Viết phương trình đường thẳng đi qua I và vuông góc với .
+) Gọi , tìm tọa độ điểm K, K chính là tâm đường tròn (C).
+) Tính khoảng cách , từ đó suy ra bán kính của đường tròn (C): .
Lời giải:
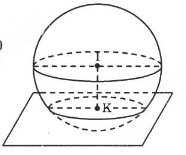
Mặt cầu có tâm và bán kính .
Khoảng cách từ tâm của mặt cầu đến mặt phẳng là:
=
Gọi là bán kính đường tròn (C), áp dụng định lí Pitago ta có:
Tâm của đường tròn là hình chiếu vuông góc của tâm của mặt cầu trên mặt phẳng .
Mặt phẳng có vectơ pháp tuyến .
Đường thẳng qua và vuông góc với nhận làm vectơ chỉ phương và có phương trình :
nên thay tọa độ điểm K vào phương trình mặt phẳng ta có:
a) Tìm giao điểm của đường thẳng và mặt phẳng .
b) Viết phương trình mặt phẳng chứa điểm và vuông góc với đường thẳng .
Phương pháp giải:
a) Tham số hóa tọa độ điểm M dạng , thay điểm M vào phương trình mặt phẳng .
b) . Viết phương trình mặt phẳng đi qua N và nhận là 1 VTPT.
Lời giải:
a) Vì nên , thay vào phương trình , ta có:
.
b) Vectơ là vectơ chỉ phương của . Mặt phẳng vuông góc với nhận làm vectơ pháp tuyến. Vì nên phương trình có dạng:
hay
a) Viết phương trình mặt phẳng chứa điểm và vuông góc với giá của .
b) Tìm giao điểm của và .
c) Viết phương trình đường thẳng đi qua điểm , vuông góc với giá của và cắt đường thẳng .
Phương pháp giải:
a) Viết phương trình mặt phẳng biết điểm đi qua và 1 VTPT.
b) Tham số hóa tọa độ giao điểm và thay vào phương trình mặt phẳng .
c) Đường thẳng đi qua A vuông góc với giá của và cắt đường thẳng d chính là đường thẳng AM.
Lời giải:
a) Mặt phẳng vuông góc với giá của nhận làm vectơ pháp tuyến; đi qua có phương trình:
b) Gọi
Thay tọa độ điểm M vào phương trình ta có:
.
Từ đây ta tính được toạ độ giao điểm của và : .
c) Đường thẳng đi qua A và vuông góc với giá của nên . Hơn nữa cắt d nên đi qua M.
Do đó đường thẳng cần tìm chính là đường thẳng nhận vectơ làm vectơ chỉ phương.
Phương trình đường thẳng :
(S):
và song song với hai đường thẳng
Phương pháp giải:
+) Gọi lần lượt là VTCP của hai đường thẳng d và d'. Khi đó mặt phẳng nhận là 1 VTPT.
+) Xác định tâm I và bán kính R của mặt cầu (S), mặt phẳng tiếp xúc với mặt cầu (S)
Lời giải:
Đường thẳng có vectơ chỉ phương
có vectơ chỉ phương
Mặt phẳng song song với và nhận vectơ làm vectơ pháp tuyến.
Phương trình mặt phẳng có dạng:
Mặt cầu có tâm và bán kính .
Để tiếp xúc với mặt cầu , ta phải có:
Ta được hai mặt phẳng thoả mãn yêu cầu:
+)
+)
Bài 9 trang 93 SGK Hình học 12: Trong hệ toạ độ , tìm toạ độ điểm là hình chiếu vuông góc của điểm trên mặt phẳngPhương pháp giải:
Điểm , hình chiếu vuông góc của điểm trên mp chính là giao điểm của đường thẳng đi qua và vuông góc với .
Lời giải:
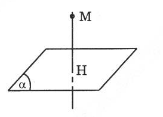
Điểm , hình chiếu vuông góc của điểm trên mp chính là giao điểm của đường thẳng đi qua và vuông góc với . Mặt phẳng có vectơ pháp tuyến .
Đường thẳng đi qua M và vuông góc với mp nhận làm vectơ chỉ phương.
Phương trình tham số của :
. thay các tọa độ điểm H vào phương trình , ta có:
Từ đây ta được .
Bài 10 trang 93 SGK Hình học 12: Trong hệ toạ độ , cho điểm và mặt phẳng . Tìm toạ độ điểm đối xứng với qua .Phương pháp giải:
Gọi là hình chiếu vuông góc của lên mặt phẳng và là điểm đối xứng của qua thì là trung điểm của đoạn thẳng .
+) Xác định tọa độ hình chiếu H của M trên mặ phẳng .
+) Xác định tọa độ điểm M':
Lời giải:
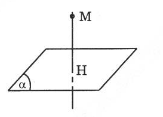
Gọi là hình chiếu vuông góc của lên mặt phẳng và là điểm đối xứng của qua thì là trung điểm của đoạn thẳng . Xét đường thẳng qua và vuông góc với .
Phương trình đi qua M và nhận là 1 VTCP có dạng:
Gọi
Thay tọa độ điểm H vào phương trình ta được:
và đối xứng nhau qua nên H là trung điểm của MM'
Bài 11 trang 93 SGK Hình học 12: Viết phương trình đường thẳng vuông góc với mặt phẳng toạ độ và cắt hai đường thẳngPhương pháp giải:
- Gọi tọa độ hai giao điểm lần lượt thuộc hai đường thẳng theo tham số .
- Lập hệ phương trình ẩn dựa vào điều kiện nên và .
Lời giải:
Gọi là điểm thuộc đường thẳng , toạ độ của là . là điểm thuộc đường thẳng , toạ độ của là .
Ta có:
Vì nên và
có vectơ chỉ phương ;
có vectơ chỉ phương .
(1)
(1)
Từ (1) và (2) ta có hệ
và được toạ độ của M , N
Từ đây ta có và được phương trình đường thẳng đi qua M và nhận làm 1 VTCP là:
Bài 12 trang 93 SGK Hình học 12: Trong hệ toạ độ , tìm toạ độ điểm đối xứng với điểm qua đường thẳng có phương trìnhPhương pháp giải:
+) Xác định tọa độ điểm H là hình chiếu của A trên đường thẳng .
- Gọi (P) là mặt phẳng đi qua A và vuông góc với . Tìm phương trình mặt phẳng (P).
- Khi đó H là giao điểm của và mặt phẳng (P).
+) Điểm M' đối xứng với M qua khi và chỉ khi H là trung điểm của MM', từ đó suy ra tọa độ điểm M'.
Lời giải:
Gọi là hình chiếu của trên .
Có ,
Vì A' đối xứng với A qua nên H là trung điểm của AA'. Ta có:
Cách khác:
Ta có thể tìm tọa độ điểm như sau:
Gọi là hình chiếu vuông góc của lên đường thẳng . Khi đó là trung điểm của .
Xét mặt phẳng qua và . Khi đó .
Vì là vectơ chỉ phương của nên là vectơ pháp tuyến của .
Phương trình mặt phẳng có dạng: hay (1)
, thay tọa độ điểm H vào phương trình mặt phẳng (P) ta có:
.
Bài tập trắc nghiệm (trang 94 - 97 SGK Hình học 12)
Trong các mệnh đề sau, mệnh đề nào sai?
(A) ; (B) ;
(C) ; (D) .
Phương pháp giải:
Lời giải:
Ta có:
Do đó A đúng, B đúng, C đúng, D sai.
Chọn (D).
, và .
Trong các mệnh đề sau, mệnh đề nào đúng?
(A)
(B) cùng phương;
(C) cos (, )= ;
(D) + + =
Phương pháp giải:
cùng phương ()
Lời giải:
A sai.
Dễ thấy không tồn tại hằng số để nên B sai.
C đúng.
sai.
Chọn (C).
Bài 3 trang 94 SGK Hình học 12: Trong không gian cho ba vectơ , vàCho hình bình hành có = , ( là gốc toạ độ). Toạ độ của tâm hình bình hành là:
(A) (B)
(C) (D) .
Phương pháp giải:
Gọi I là tâm hình bình hành OADB ta có:
Lời giải:
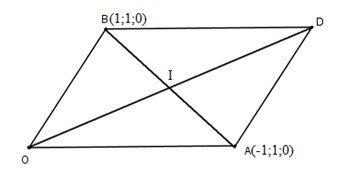
Gọi là tâm của hình bình hành ta có:
Vậy
Chọn (A).
Cách khác:
Vì là tâm hình bình hành nên là trung điểm
Bài 4 trang 94 SGK Hình học 12: Trong không gian cho bốn điểm và
Trong các mệnh đề sau, mệnh đề nào sai?
(A) Bốn điểm A, B, C, D tạo thành một tứ diện ;
(B) Tam giác ABD là tam giác đều ;
(C) ;
(D) Tam giác là tam giác vuông.
Phương pháp giải:
a) Chứng minh 4 điểm A, B, C, D không đồng phẳng.
b) Chứng minh AB = BD = DA
c) Kiểm tra tích vô hướng
d) Kiểm tra trong các điều kiện
Lời giải:
Ta có: phương trình đoạn chắn mặt phẳng (ABC) là: .
Dễ thấy điểm D không thuộc (ABC) nên bốn điểm A, B, C, D không đồng phẳng.
Mệnh đề A đúng.
Ta có:
Do đó tam giác ABD đều, mệnh đề B đúng.
Mệnh đề C đúng.
Chọn (D)
Gọi lần lượt là trung điểm của và . Toạ độ điểm là trung điểm của là:
(A) G ; (B) G ;
(C) G ; (D) G .
Phương pháp giải:
, điểm M là trung điểm của AB .
Lời giải:
M là trung điểm của AB
N là trung điểm của CD
G là trung điểm của MN
Chọn (D)
Bài 6 trang 95 SGK Hình học 12: Trong không gian cho bốn điểm vàMặt cầu ngoại tiếp tứ diện có bán kính là:
(A) ; (B) ;
(C) ; (D) .
Phương pháp giải:
Gọi phương trình tổng quát của mặt cầu ngoại tiếp tứ diện ABCD là:
Thay tọa độ các điểm A, B, C, D vào phương trình mặt cầu tìm các hệ số a, b, c, d.
Suy ra bán kính của mặt cầu:
Lời giải:
Phương trình tổng quát của mặt cầu ngoại tiếp tứ diện ABCD là:
Mặt cầu đi qua nên ta có hệ:
Lấy ta được:
Thế lần lượt vào các phương trình (1), (2), (3), (4) ta suy ra:
Vậy bán kính
Chọn (A).
Bài 7 trang 95 SGK Hình học 12: Cho mặt phẳng đi qua điểm và song song với giá của hai vectơ và .Phương trình của mặt phẳng là:
(A) ;
(B) ;
(C) ;
(D) .
Phương pháp giải:
Gọi là véc tơ pháp tuyến của mặt phẳng thì .
Lời giải:
Gọi là véc tơ pháp tuyến của mặt phẳng thì
.
Phương trình của mặt phẳng là:
Chọn (B)
Bài 8 trang 95 SGK Hình học 12: Cho ba điểm . Phương trình mặt phẳng là:(A)
(B)
(C)
(D) .
Phương pháp giải:
Véc tơ pháp tuyến của mặt phẳng là:
Lời giải:
Véc tơ pháp tuyến của mặt phẳng là:
Phương trình mặt phẳng là:
Chọn (B).
Bài 9 trang 95 SGK Hình học 12: Gọi là mặt phẳng cắt ba trục toạ độ tại điểm . Phương trình của là:
(A) ;
(B) ;
(C) ;
(D) .
Phương pháp giải:
Phương trình mặt phẳng đi qua các điểm có dạng phương trình đoạn chắn:
Lời giải:
Phương trình mặt phẳng dưới dạng đoạn chắn là:
Chọn (D).
Trong các mệnh đề sau, mệnh đề nào sai?
(A) ; (B) ;
; (D) .
Phương pháp giải:
cùng phương.
Lời giải:
Ta có:
Vậy các mệnh đề A, B, D đúng.
Chọn (C).
;
; .
Phương pháp giải:
Đường thẳng d đi qua và có VTCP có phương trình tham số:
Lời giải:
Ta có: cũng là VTCP của đường thẳng .
Vậy phương trình tham số của đường thẳng là:
Chọn (C)
Phương trình tham số của d là:
(A);
(B);
(C);
(D)
Phương pháp giải:
Đường thẳng vuông góc với mặt phẳng nên có véc tơ chỉ phương là:
Lời giải:
Đường thẳng vuông góc với mặt phẳng nên có véc tơ chỉ phương là:
Phương trình tham số của là:
Chọn (B)
Bài 13 trang 96 SGK Hình học 12: Cho hai đường thẳngvà
Trong các mệnh đề sau, mệnh đề nào đúng?
(A) d1⊥ d2 (B) d1 // d2
(C) d1 ≡ d2 (D) d1 và d2 chéo nhau.
Phương pháp giải:
Gọi lần lượt là VTCP của .
Nếu cùng phương thì hoặc song song hoặc trùng nhau.
Lấy M bất kì thuộc ,
Nếu
Nếu
Lời giải:
Ta có:
Lấy , ta dễ thấy .
Vậy .
Chọn (C).
Trong các mệnh đề sau, mệnh đề nào đúng?
(A) ;
(B) cắt ;
(C) ;
(D) .
Phương pháp giải:
Gọi lần lượt là VTPT của và VTCP của đường thẳng d. Kiểm tra mối quan hệ giữa hai vector này.
Lời giải:
Mặt phẳng có véc tơ pháp tuyến
Đường thẳng có véc tơ chỉ phương
Suy ra hoặc hoặc
Chọn thay tọa độ của vào phương trình mặt phẳng ta được:
do đó
Vậy
Chọn (D)
Bán kính của là:
(A) ; (B) ; (C) ; (D) .
Phương pháp giải:
Bán kính của mặt cầu là:
Lời giải:
Bán kính của mặt cầu là:
Chọn (A).
Các dạng toán về đường thẳng và mặt phẳng1. Kiến thức cần nhớ
a) Phương trình mặt phẳng.
Mặt phẳng đi qua điểm và có VTPT thì có phương trình:
b) Phương trình đường thẳng.
Đường thẳng đi qua điểm và nhận làm VTCP thì có phương trình tham số
c) Giao tuyến của hai mặt phẳng.
Phương trình tổng quát của đường thẳng:
ở đó là các VTPT của hai mặt phẳng có phương trình như trên.
Khi đó là VTCP của đường thẳng.
d) Vị trí tương đối của đường thẳng và mặt phẳng.
Cho đường thẳng có VTCP và mặt phẳng có VTPT . Khi đó:
+)
+)
+) cùng phương với
+) cắt thì tọa độ giao điểm thỏa mãn
2. Một số dạng toán thường gặp
Dạng 1: Tìm giao điểm của đường thẳng và mặt phẳng.
Phương pháp:
- Gọi tọa độ của giao điểm theo tham số của đường thẳng.
- Thay tọa độ vào phương trình mặt phẳng, tìm tham số suy ra điểm cần tìm.
Dạng 2: Xét vị trí tương đối của đường thẳng và mặt phẳng.
Phương pháp:
- Tìm các VTPT của mặt phẳng, VTCP của đường thẳng.
- Dựa vào mối quan hệ của để kết luận:
+ Nếu cùng phương thì
+ Nếu có phương vuông góc thì hoặc
Trường hợp sẽ xảy ra nếu thêm điều kiện một điểm thuộc thì thuộc .
Dạng 3: Viết phương trình mặt phẳng.
Phương pháp:
- Tìm tọa độ điểm đi qua.
- Tìm một VTPT của mặt phẳng.
- Viết phương trình mặt phẳng đi qua một điểm và có VTPT tìm được ở trên.
Một số dạng phương trình mặt phẳng:
+) Đi qua một điểm và vuông góc với đường thẳng.
Viết phương trình mặt phẳng đi qua và vuông góc với đường thẳng .
- Mặt phẳng đi qua và vuông góc với đường thẳng thì nhận làm VTPT.
+) Đi qua một điểm và song song với hai đường thẳng khác.
Viết phương trình mặt phẳng đi qua và song song với đường thẳng .
- song song với đường thẳng nên nhận làm VTPT.
+) Đi qua hai điểm và song song với đường thẳng.
Viết phương trình mặt phẳng đi qua hai điểm và song song với đường thẳng .
- đi qua và song song với đường thẳng nên nó đi qua và nhận
Dạng 4: Viết phương trình đường thẳng.
Phương pháp:
- Tìm tọa độ điểm đi qua.
- Tìm một VTCP của đường thẳng.
- Viết phương trình đường thẳng đi qua một điểm và có VTCP như trên.
Một số dạng phương trình đường thẳng liên quan đến mặt phẳng.
+) Đi qua một điểm và vuông góc với một mặt phẳng.
Viết phương trình đường thẳng đi qua điểm và vuông góc với mặt phẳng
- Đường thẳng đi qua và vuông góc với mặt phẳng thì nó nhận làm VTCP.
+) Hình chiếu của một đường thẳng trên một mặt phẳng.
- Viết phương trình mặt phẳng chứa và vuông góc với
( đi qua điểm và nhận làm VTPT).
- Đường thẳng là giao tuyến của hai mặt phẳng nên
+) Đường thẳng đi qua một điểm, vuông góc với đường thẳng và song song với mặt phẳng.
Viết phương trình đường thẳng đi qua , vuông góc với và song song với mặt phẳng .
-
1. Kiến thức cần nhớ
- Dạng 1: Phương trình chính tắc của mặt cầu tâm và bán kính là:
(1)
- Dạng 2: Phương trình tổng quát của mặt cầu (2)
Phương trình (2) có tâm và bán kính .
Do đó điều kiện cần và đủ để (2) là phương trình mặt cầu là
2. Một số dạng toán thường gặp
Dạng 1: Nhận biết các yếu tố từ phương trình mặt cầu.
Phương pháp:
Sử dụng định nghĩa tâm và bán kính mặt cầu:
- Mặt cầu có phương trình dạng có tâm và bán kính .
- Mặt cầu có phương trình dạng có tâm và bán kính .
Dạng 2: Viết phương trình mặt cầu.
Phương pháp chung:
Cách 1: Sử dụng phương trình mặt cầu dạng tổng quát.
- Tìm tâm và bán kính mặt cầu, từ đó viết phương trình theo dạng 1 nêu ở trên.
Cách 2: Sử dụng phương trình mặt cầu dạng khai triển.
- Gọi mặt cầu có phương trình
- Sử dụng điều kiện bài cho để tìm .
Một số bài toán hay gặp:
- Viết phương trình mặt cầu với tâm và bán kính đã cho.
- Mặt cầu có đường kính : tâm là trung điểm của và bán kính .
- Mặt cầu đi qua điểm :
* Cách 1:
+) Gọi mặt cầu có phương trình
+) Thay tọa độ các điểm bài cho vào phương trình và tìm .
*Cách 2:
+) Gọi I(a,b,c) là tâm của mặt cầu.
+) Lập hệ phương trình
tìm a, b, c.
+) Bán kính .
* Cách 3:
+) Tìm mặt phẳng trung trực của các đoạn thẳng AB, AC, AD. Mặt phẳng trung trực của AB đi qua trung điểm của AB và nhận AB làm một vectơ pháp tuyến.
+) Tâm mặt cầu là giao của 3 mặt phẳng đó.
+) Bán kính .
Dạng 3: Tìm tham số để mặt cầu thỏa mãn điều kiện cho trước.
- Mặt cầu đi qua một điểm nếu tọa độ điểm đó thỏa mãn phương trình mặt cầu.
1. Kiến thức cần nhớ
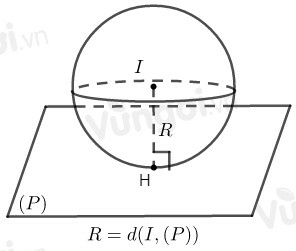
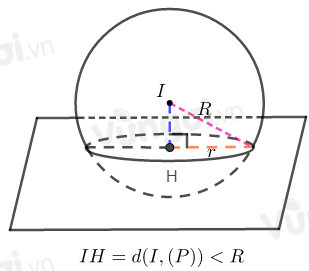
Cho mặt phẳng và mặt cầu tâm bán kính . Khi đó:
-
-
ở đó, là tiếp điểm, là tiếp diện và tại
-
ở đó : với là hình chiếu của trên .
Đặc biệt: hay đi qua thì
được gọi là đường tròn lớn, là mặt phẳng kính.
2. Một số dạng toán thường gặp
Dạng 1: Viết phương trình mặt cầu tiếp xúc hoặc cắt mặt phẳng cho trước.
Phương pháp:
- Bước 1: Tính bán kính mặt cầu dựa vào các điều kiện bài cho:
+ Tiếp xúc mặt phẳng nếu
+ Cắt mặt phẳng theo giao tuyến và đường tròn bán kính thì
- Bước 2: Viết phương trình mặt cầu biết tâm và bán kính.
Dạng 2: Viết phương trình mặt phẳng tiếp xúc, giao với mặt cầu cho trước.
Phương pháp:
- Bước 1: Tìm VTPT của mặt phẳng dựa vào điều kiện bài cho.
+ Tiếp xúc mặt cầu tại điểm thì
+ Trường hợp song song với mặt phẳng ( là các số cho trước) và cắt mặt cầu theo đường tròn có bán kính thì tức là .
và .
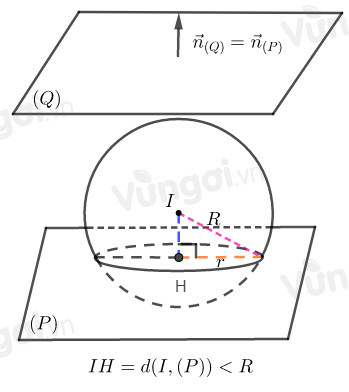
- Bước 2: Viết phương trình mặt phẳng.
+ Tiếp xúc mặt cầu tại điểm : Xác định điểm rồi lập phương trình mặt phẳng.
+ Trường hợp song song với mặt phẳng ( là các số cho trước) và cắt mặt cầu theo đường tròn có bán kính :
Sử dụng để tìm d'.
1. Kiến thức cần nhớ
Cho mặt cầu tâm , bán kính và đường thẳng (đi qua và có VTCP ). Khi đó:
+) .
+) .
+) .
ở đó và
2. Một số dạng toán thường gặp
Dạng 1: Xét vị trí tương đối của đường thẳng và mặt cầu.
Phương pháp:
Cách 1: Sử dụng lý thuyết vị trí tương đối của đường thẳng và mặt cầu.
- Bước 1: Tính khoảng cách từ tâm mặt cầu đến đường thẳng và so sánh với .
- Bước 2: Kết luận dựa vào các vị trí tương đối của đường thẳng và mặt cầu.
Cách 2: Xét phương trình giao điểm của đường thẳng và mặt cầu.
- Nếu phương trình vô nghiệm thì đường thẳng không có điểm chung với mặt cầu.
- Nếu phương trình có nghiệm duy nhất thì đường thẳng tiếp xúc với mặt cầu.
- Nếu phương trình có hai nghiệm phân biệt thì đường thẳng cắt mặt cầu tại hai điểm phân biệt.
Dạng 2: Viết phương trình mặt cầu có tâm và tiếp xúc với đường thẳng cho trước.
Phương pháp:
- Bước 1: Gọi phương trình mặt cầu ở dạng tổng quát.
- Bước 2: Xét phương trình giao điểm của và , điều kiện để mặt cầu tiếp xúc với đường thẳng là phương trình giao điểm có nghiệm duy nhất.
Dạng 3: Viết phương trình mặt phẳng có mối quan hệ với đường thẳng và mặt cầu.
Phương pháp chung:
Xác định điểm đi qua và VTPT của mặt phẳng, từ đó viết phương trình.

