Chúng tôi giới thiệu Giải bài tập Toán lớp 12 Bài 1: Sự đồng biến, nghịch biến của hàm số chính xác, chi tiết nhất giúp học sinh dễ dàng làm bài tập Sự đồng biến, nghịch biến của hàm số lớp 12.
Giải bài tập Toán lớp 12 Bài 1: Sự đồng biến, nghịch biến của hàm số
Trả lời câu hỏi giữa bài
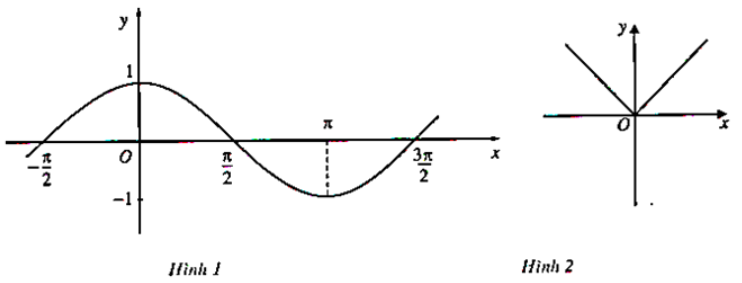
Phương pháp giải:
- Trên khoảng K: đồ thị hàm số đi lên (từ trái sang phải) thì hàm số đồng biến trên K.
- Trên khoảng K: đồ thị hàm số đi xuống (từ trái sang phải) thì hàm số nghịch biến trên K.
Lời giải:
- Hàm số trên đoạn
Các khoảng tăng:
Các khoảng giảm: .
- Hàm số trên khoảng
Khoảng tăng:
Khoảng giảm
a) (H.4a)

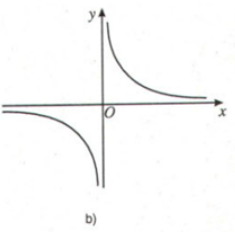
Xét dấu đạo hàm của hàm số và điền vào bảng tương ứng.
Phương pháp giải:
Quan sát đồ thị, nhận xét khoảng đồ thị đi lên (đồng biến) hay đi xuống (nghịch biến), từ đó suy ra dấu của đạo hàm:
Trên từng khoảng, nếu đồ thị hàm số đi lên (từ trái qua phải) thì hàm số đồng biến trên khoảng đó, đồng thời đạo hàm mang dấu (+) trên khoảng đó.
Ngược lại, nếu đồ thị hàm số đi xuống(từ trái qua phải) thì hàm số nghịch biến trên khoảng đó, đồng thời đạo hàm mang dấu (-) trên khoảng ấy.
Lời giải:
a)
Quan sát đồ thị, dễ thấy:
- Trên khoảng : đồ thị hàm số đi lên (từ trái qua phải) nên hàm số đồng biến trên , và .
- Trên khoảng , đồ thị hàm số đi xuống (từ trái qua phải) nên hàm số nghịch biến trên , và .
Bảng xét dấu:
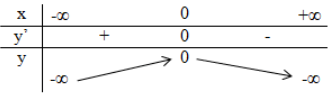
Quan sát đồ thị ta thấy:
- Tại thì không có giá trị của nên hàm số không xác định tại
- Trên mỗi khoảng và thì đồ thị đi xuống (từ trái qua phải) nên hàm số nghịch biến trên mỗi khoảng này.
Khi đó và
Bảng xét dấu:
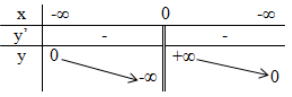
Lời giải:
Xét hàm số có đạo hàm với mọi số thực và hàm số đồng biến trên toàn bộ (quan sát đồ thị).
Vậy nếu hàm số đồng biến (nghịch biến) trên thì đạo hàm của nó không nhất thiết phải dương (âm) trên đó.
Phương pháp giải:
+) Tìm tập xác định của hàm số.
+) Tính đạo hàm của hàm số. Tìm các điểm xi (I =1,2,3,…,n) mà tại đó đạo hàm bằng 0 hoặc không xác định
+) Sắp xếp các điểm xi theo thứ tự tăng dần và lập bảng biến thiên
+) Dựa vào bảng biến thiên để kết luận khoảng đồng biến và nghịch biến của hàm số trên tập xác định của nó. (nếu y’ > 0 thì hàm số đồng biến, nếu y’ < 0 thì hàm số nghịch biến)
Chú ý: Khi kết luận các khoảng đồng biến và nghịch biến của hàm số ta nhớ sử dụng chữ và chứ không được sử dụng kí hiệu hợp.
a)
Tập xác định:
Có
Bảng biến thiên:
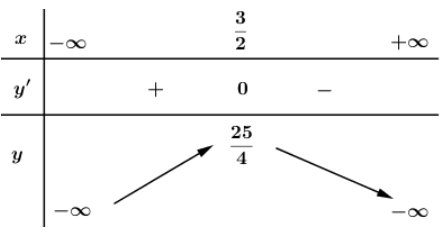
Vậy hàm số đồng biến trên khoảng và nghịch biến trên khoảng
b)
Tập xác định:
Có
Bảng biến thiên:
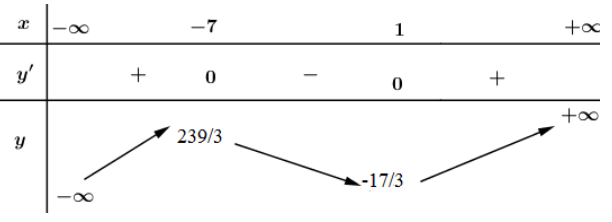
Vậy hàm số đồng biến trên các khoảng và .
Hàm số nghịch biến trên
c)
Tập xác định:
Có
Bảng biến thiên:
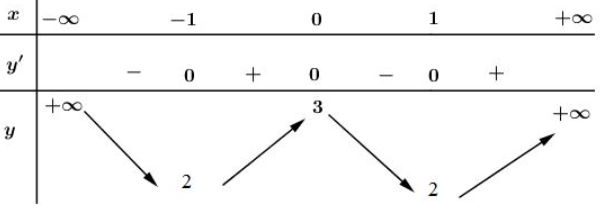
Vậy hàm số đồng biến trên các khoảng và
Hàm số nghịch biến trên các khoảng và
d)
Tập xác định:
Có
Bảng biến thiên:
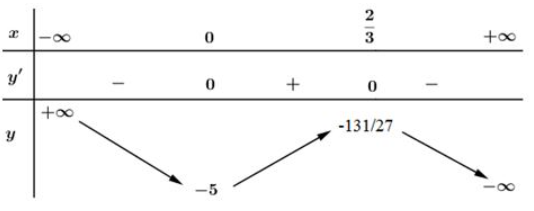
Vậy hàm số đồng biến trên khoảng
Hàm số nghịch biến trên các khoảng và
a) ;
Phương pháp giải:
+) Tìm tập xác định của hàm số.
+) Tính đạo hàm của hàm số. Tìm các điểm xi (I =1,2,3,…,n) mà tại đó đạo hàm bằng 0 hoặc không xác định
+) Sắp xếp các điểm xi theo thứ tự tăng dần và lập bảng biến thiên
+) Dựa vào bảng biến thiên để kết luận khoảng đồng biến và nghịch biến của hàm số trên tập xác định của nó. (nếu y’ > 0 thì hàm số đồng biến, nếu y’ < 0 thì hàm số nghịch biến)
Ở bài toán này cần chú ý các tập xác định của hàm số.
Lời giải:
a)
Tập xác định:
Có:
Bảng biến thiên:
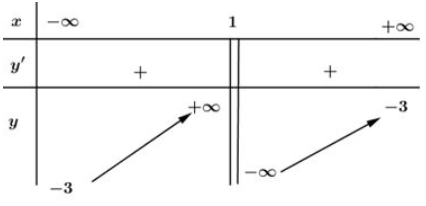
Vậy hàm số đồng biến trên các khoảng xác định của nó là: và
Chú ý: Cách tính giới hạn để điền vào BBT:
b)
Tập xác định:
Có:
Bảng biến thiên:
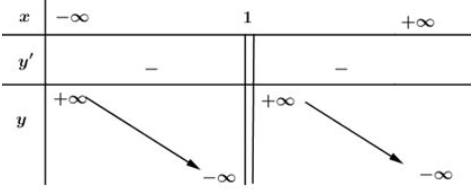
Vậy hàm số nghịch biến trên các khoảng xác định của nó là: và
Chú ý: Cách tính giới hạn để điền vào bảng biến thiên:
c)
Có
Tập xác định:
Có
Bảng biến thiên:

Vậy hàm số nghịch biến trên khoảng và đồng biến trên khoảng
Chú ý: Cách tính giới hạn để điền vào BBT:
d)
Có
Tập xác định:
Có:
Bảng biến thiên:

Vậy hàm số nghịch biến trên các khoảng xác định của nó là: và
Chú ý: Cách tính giới hạn để điền vào BBT:
Phương pháp giải:
+) Tìm tập xác định của hàm số.
+) Tính đạo hàm của hàm số. Tìm các điểm xi (i =1,2,3,…,n) mà tại đó đạo hàm bằng 0 hoặc không xác định
+) Xét dấu đạo hàm và kết luận khoảng đồng biến nghịch biến.
Lời giải:
Tập xác định:
Có:
Ta có:
Hàm số đồng biến trên khoảng
Hàm số nghịch biến trên khoảng và
Phương pháp giải:
+) Tìm tập xác định của hàm số.
+) Tính đạo hàm của hàm số. Tìm các điểm xi (I =1,2,3,…,n) mà tại đó đạo hàm bằng 0 hoặc không xác định
+) Xét dấu đạo hàm và kết luận khoảng đồng biến nghịch biến.
Lời giải:
ĐK:
Tập xác định:
Có
+) nên hàm số đồng biến trên khoảng .
+) nên hàm số nghịch biến trên khoảng
b)
Phương pháp giải:
+) Chuyển vế tất cả các biểu thức chứa biến sang vế trái sau đó so sánh hàm số với 0.
+) Tính đạo hàm bậc nhất của hàm số và khảo sát hàm số trên các khoảng đề bài đã cho.
+) Dựa vào tính đơn điệu của hàm số để kết luận bài toán.
Lời giải:
a)
Xét hàm số: với
Ta có:
Vậy hàm số luôn đồng biến trên
b)
Xét hàm số: với
Ta có:
Với nên ta có: và (theo câu a)
Vậy hàm số đồng biến trên
Kí hiệu K là một khoảng, một đoạn hoặc một nửa khoảng.
1. Định nghĩa
Hàm số y = f(x) đồng biến (tăng) trên K ⇔ ∀x1, x2 ∈ K, x1 < x2 thì f(x1) < f(x2).
Hàm số y = f(x) nghịch biến (giảm) trên K ⇔ ∀x1, x2 ∈ K, x1 < x2 thì f(x1) > f(x2).
2. Điều kiện cần để hàm số đơn điệu
Cho hàm số f có đạo hàm trên K.
- Nếu f đồng biến trên K thì f'(x) ≥ 0 với mọi x ∈ K.
- Nếu f nghịch biến trên K thì f'(x) ≤ 0 với mọi x ∈ K.
3. Điều kiện đủ để hàm số đơn điệu
Cho hàm số f có đạo hàm trên K.
- Nếu f'(x) > 0 với mọi x ∈ K thì f đồng biến trên K.
- Nếu f'(x) < 0 với mọi x ∈ K thì f nghịch biến trên K.
- Nếu f'(x) = 0 với mọi x ∈ K thì f là hàm hằng trên K.
Định lý mở rộng
- Nếu f'(x) ≥ 0 với mọi x ∈ K và f'(x) = 0 chỉ tại một số hữu hạn điểm thuộc K thì f đồng biến trên K.
- Nếu f'(x) ≤ 0 với mọi x ∈ K và f'(x) = 0 chỉ tại một số hữu hạn điểm thuộc K thì f nghịch biến trên K.
4. Quy tắc xét tính đơn điệu của hàm số
i) Tìm tập xác định
ii) Tính đạo hàm f'(x). Tìm các điểm xi (i= 1 , 2 ,..., n) mà tại đó đạo hàm bằng 0 hoặc không xác định.
iii) Sắp xếp các điểm xi theo thứ tự tăng dần và lập bảng biến thiên.
iv) Nêu kết luận về các khoảng đồng biến, nghịch biến của hàm số.
Sơ đồ tư duy về tính đơn điệu của hàm số
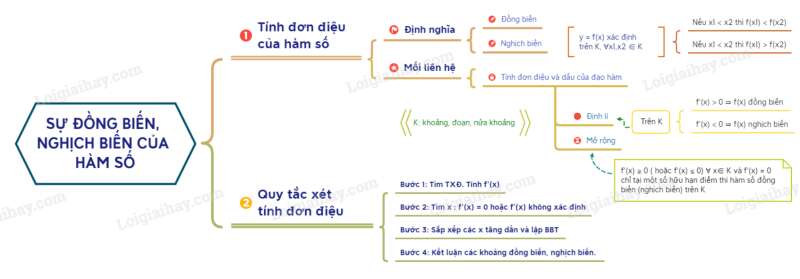
Dạng 1: Tìm các khoảng đơn điệu của hàm số.
Phương pháp:
- Bước 1: Tìm TXĐ của hàm số.
- Bước 2: Tính đạo hàm , tìm các điểm mà tại đó đạo hàm bằng hoặc không xác định.
- Bước 3: Xét dấu đạo hàm và nêu kết luận về khoảng đồng biến, nghịch biến của hàm số.
+ Các khoảng mà là các khoảng đồng biến của hàm số.
+ Các khoảng mà là các khoảng nghịch biến của hàm số.
Ví dụ 1: Tìm khoảng đồng biến, nghịch biến của hàm số .
Ta có nên hàm số đã cho đồng biến trên
nên hàm số đã cho nghịch biến trên
Một số trường hợp đặc biệt:

Dạng 2: Tìm giá trị của m để hàm số đơn điệu trên R.
Phương pháp:
- Bước 1: Tính .
- Bước 2: Nêu điều kiện của bài toán:
+ Hàm số đồng biến trên và tại hữu hạn điểm.
+ Hàm số nghịch biến trên và tại hữu hạn điểm.
- Bước 3: Từ điều kiện trên sử dụng các kiến thức về dấu của nhị thức bậc nhất, tam thức bậc hai để tìm .
Ví dụ 2: Tìm tất cả các giá trị thực của tham số sao cho hàm số đồng biến trên .
Giải: Hàm số đã cho đồng biến trên
Cho hàm số . Khi đó:
Dạng 3: Tìm m để hàm số đơn điệu trên miền D cho trước.
Phương pháp:
- Bước 1: Nêu điều kiện để hàm số đơn điệu trên D:
+ Hàm số đồng biến trên .
+ Hàm số nghịch biến trên .
- Bước 2: Từ điều kiện trên sử dụng các cách suy luận khác nhau cho từng bài toán để tìm .
Dưới đây là một trong những cách hay được sử dụng:
- Rút theo sẽ xảy ra một trong hai trường hợp: hoặc .
- Khảo sát tính đơn điệu của hàm số trên .
- Kết luận:
- Bước 3: Kết luận.
Dạng 4: Tìm m để hàm số đồng biến, nghịch biến trên khoảng
- Bước 1: Tính .
- Bước 2: Nêu điều kiện để hàm số đồng biến, nghịch biến:
+ Hàm số đồng biến trên
+ Hàm số nghịch biến trên
- Bước 3: Kết luận.

