Chúng tôi giới thiệu Giải bài tập Toán lớp 12 Bài 2: Mặt cầu chính xác, chi tiết nhất giúp học sinh dễ dàng làm bài tập Mặt cầu lớp 12.
Giải bài tập Toán lớp 12 Bài 2: Mặt cầu
Trả lời câu hỏi giữa bài
Lời giải:
Do tâm mặt cầu cách đều hai điểm A, B nên tập hợp tâm cần tìm chính là tập hợp các điểm cách đều hai điểm A, B.
Tập hợp tâm các mặt cầu luôn luôn đi qua hai điểm cố định A và B cho trước là mặt phẳng trung trực của đoạn thẳng AB.
Trả lời câu hỏi 2 trang 45 SGK Hình học 12: a) Hãy xác định đường tròn giao tuyến của mặt cầu S(O; r) và mặt phẳng (α) biết rằng khoảng cách từ tâm O đến (α) bằngb) Cho mặt cầu S(O; r), hai mặt phẳng (α) và (β) có khoảng cách đến tâm O của mặt cầu đã cho lần lượt là a và b (0 < a < b < r). Hãy so sánh hai bán kính của các đường tròn giao tuyến.
Phương pháp giải:
- Dựng hình, tính bán kính của từng đường tròn giao tuyến bằng cách áp dụng định lý Pi-ta-go.
- Từ đó kết luận cho từng câu a, b.
Lời giải:
a)
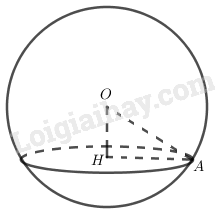
Xét tam giác vuông tại có nên: .
Vậy đường tròn giao tuyến có bán kính .
b)
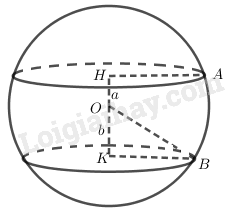
Xét tam giác vuông tại có
Xét tam giác vuông tại có
Mà nên hay .
Vậy đường tròn cắt bởi có bán kính nhỏ hơn bán kính đường tròn cắt bởi .
a) Đi qua đỉnh của hình lập phương.
b) Tiếp xúc với cạnh của hình lập phương.
c) Tiếp xúc với mặt của hình lập phương.
Lời giải:
a) Tâm mặt cầu là giao điểm các đường chéo chính.
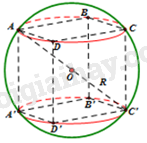
Bán kính mặt cầu là
Đường chéo hình vuông cạnh là
Xét tam giác vuông tại :
Ta có:
Do đó .
Vậy bán kính mặt cầu đi qua đỉnh hình lập phương cạnh là .
b)

Vì ABCDA'B'C'D' là hình lập phương nên các tứ giác: ABC’D’ , BCD’A’, CDA’B’, DAB’C’, AA’C’C, BB’D’D là các hình chữ nhật bằng nhau.
Xét hình chữ nhật ABC’D’ ta có:
O là trung điểm của AC’ và BD’
Tương tự ta cũng chứng minh được khoảng cách từ O đến các cạnh còn lại là
Suy ra tồn tại mặt cầu tâm O, bán kính tiếp xúc với 12 cạnh.
Vậy mặt cầu tiếp xúc với 12 cạnh của hình lập phương.
c) Tâm mặt cầu tiếp xúc mặt của hình lập phương là trung điểm của đường nối hai tâm đáy.
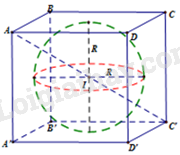
Bán kính mặt cầu là
Dựng hình, nhận xét cạnh hình lập phương và tính thể tích.
Lời giải:

Hình lập phương ngoại tiếp mặt cầu bán kính có cạnh bằng
Thể tích hình lập phương đó là: .
Câu hỏi và bài tập (trang 49 SGK Hình học 12)Phương pháp giải:
+) Trong tam giác vuông có đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền.
+) Tâm đường tròn ngoại tiếp tam giác tam giác vuông là trung điểm của cạnh huyền.
Lời giải:
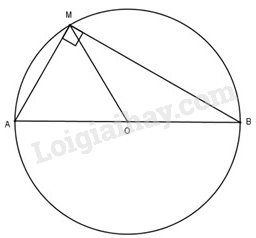
Gọi là trung điểm đoạn thẳng , vì tam giác vuông tại nên trung tuyến bằng nửa cạnh huyền, tức .
Vậy tập hợp các điểm nhìn dưới một góc vuông nằm trên mặt cầu đường kính
Ngược lại, lấy thuốc mặt cầu đường kính thì .
Do đó nếu khác và thì tam giác vuông tại , còn khi hoặc ta cũng coi nhìn một góc vuông.
Kết luận: Tập hợp các điểm trong không gian nhìn đoạn thẳng dưới một góc vuông là mặt cầu đường kính .
Phương pháp giải:
+) Sử dụng đính lý Pi-ta-go để tính các cạnh và tìm tâm, tính bán kính của mặt cầu ngoại tiếp khối chóp.
Lời giải:
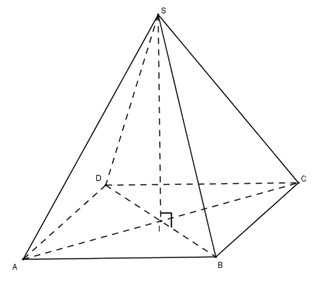
Gọi .
Ta có ABCD là hình vuông cạnh nên ta có:
có nên là tam giác vuông cân tại .
Tương tự tam giác SBD cũng vuông cân tại S.
Vậy mặt cầu ngoại tiếp hình chóp có tâm và bán kính
Cách khác:
Có thể tính IS như sau:
Từ đó ta cũng kết luận được I là tâm mặt cầu ngoại tiếp hình chóp và bán kính bằng .
Sử dụng các tính chất của mặt cầu để làm bài.
Lời giải:
Gọi O là tâm của mặt cầu chứa đường tròn (C) cố định cho trước.
⇒ O cách đều tất cả các điểm M thuộc đường tròn (C)
⇒ O nằm trên đường thẳng đi qua tâm của đường tròn (C) và vuông góc với mặt phẳng chứa (C).
Kết luận: Tập hợp tâm các mặt cầu luôn luôn chứa một đường tròn cố định cho trước là đường thẳng vuông góc với mặt phẳng chứa đường tròn tại tâm của nó.
Bài 4 trang 49 SGK Hình học 12: Tìm tập hợp tâm những mặt cầu luôn cùng tiếp xúc với ba cạnh của một tam giác cho trước.
Lời giải:
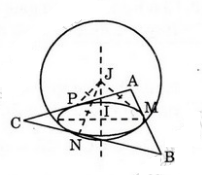
* Lấy một mặt cầu bất kì (S) thỏa mãn ycđb.
Giả sử (S) có tâm J, bán kính R và tiếp xúc với ba cạnh: lần lượt tại .
Gọi I là hình chiếu vuông góc của J lên mp . Ta sẽ chứng minh I là tâm đường tròn nội tiếp tam giác ABC.
* Ta có: (định lí 3 đường vuông góc)
Chứng minh tương tự có: (1)
* Xét ba tam giác có:
chung
⇒ (ch- cgv)
⇒ (2)
Từ (1) và (2) suy ra, I là tâm đường tròn nội tiếp tam giác ABC.
Vậy J thuộc đường thẳng d qua I, vuông góc với mp (ABC)
* Ngược lại lấy điểm J bất kì thuộc d, ta chứng minh tồn tại mặt cầu tâm J tiếp xúc với 3 cạnh của tam giác ABC.
Gọi lần lượt là hình chiếu của I xuống 3 cạnh
Ta có:
(1)
Mặt khác; .
⇒ (c-g-c)
⇒ (2)
Từ (1) và (2) suy ra, mặt cầu (S) tâm J, bán kính JM tiếp xúc với ba cạnh của tam giác ABC.
Vậy tập hợp tâm các mặt cầu tiếp xúc với ba cạnh của tam giác ABC cho trước là đường thẳng d đi qua tâm đường tròn ngoại tiếp của ∆ABC và vuống góc với mp (ABC)
a) Chứng minh rằng .
b) Gọi . Tính theo và .
Phương pháp giải:
+) Sử dụng các tam giác đồng dạng để chứng minh các tỉ lệ giữa các cạnh. Từ đó suy ra tích cần chứng minh.
+) Sử dụng định lý Pi-ta-go và tỉ lệ vừa chứng minh ở câu a để tính đại lượng cần tính.
Lời giải:
a)
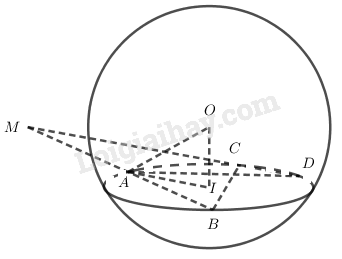
Gọi là mặt phẳng chứa hai đường thẳng đã cho. Mặt phẳng cắt mặt cầu theo một đường tròn tâm , là hình chiếu vuông góc của lên mặt phẳng .
Xét hai tam giác và có:
+) (Hai góc cùng chắn một cung)
+) chung
đồng dạng với
(các cặp cạnh tương ứng tỉ lệ).
b) Đặt , ta có vuông góc với và ta có:
Hạ vuông góc , ta có là trung điểm của .
Ta có ; .
Vậy .
+) Áp dụng tính chất của hai tiếp tuyến cắt nhau.
+) Chứng minh hai tam giác bằng nhau suy ra các góc tương ứng bằng nhau.
Lời giải: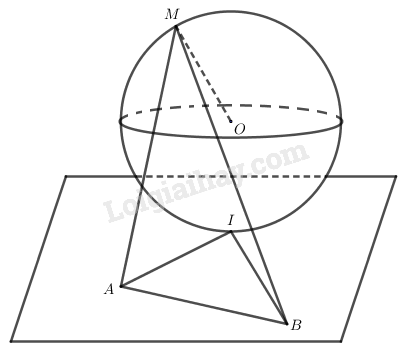
Do mặt cầu S(O; r) tiếp xúc với mp (P) tại I nên: OI ⊥ (P) ⇒ OI ⊥ IA
Suy ra, AI là tiếp tuyến của mặt cầu đã cho tại điểm I.
Theo tính chất của mặt cầu, ta có và là hai tiếp tuyến với cầu kẻ từ , cho nên , tương tự
Hai tam giác và bằng nhau (c.c.c)
(Hai góc tương ứng).
Bài 7 trang 49 SGK Hình học 12: Cho hình hộp chữ nhật có .
a) Hãy xác định tâm và bán kính của mặt cầu đi qua 8 đỉnh của hình hộp đó.
b) Tính bán kính của đường tròn là giao tuyến của mặt phẳng với mặt cầu trên.
Phương pháp giải:
a) Xác định tâm và bán kính của hình hộp dựa vào tính chất các đường chéo của hình hộp thì bằng nhau
b) Đường tròn cần tìm là đường tròn ngoại tiếp hình chữ nhật .
Lời giải:
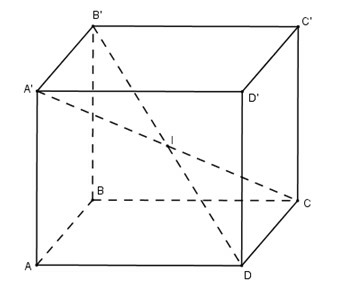
a) Trong hình hộp chữ nhật, bốn đường chéo cắt nhau tại điểm là trung điểm của mỗi đường.
Vì đường chéo trong hình hộp chữ nhật bằng nhau, nên điểm cách đều đỉnh của hình hộp chữ nhật. Nó là tâm của mặt cầu ngoại tiếp hình hộp.
Vì nên bán kính mặt cầu
vuông tại A nên theo Pitago ta có:
vuông tại B nên theo Pitago ta có:
Do đó
b) Giao tuyến của mặt phẳng với mặt cầu ngoại tiếp hình hộp chữ nhật là đường tròn ngoại tiếp hình chữ nhật . Nên bán kính của đường trong giao tuyến là:
Gọi các tiếp điểm và sử dụng tính chất tiếp tuyến cắt nhau của mặt cầu để chứng minh.
Lời giải: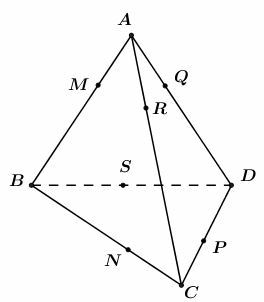
Giả sử tứ diện có mặt cầu tiếp xúc với cả cạnh của tứ diện; tiếp xúc với lần lượt tại . Vì các đoạn thẳng kẻ từ một điểm đến tiếp điểm của các tiếp tuyến đó bằng nhau, nên ta có:
Ta chứng minh: .
Ta có
Hay: .
Bài 9 trang 49 SGK Hình học 12: Cho một điểm cố định và một đường thẳng cố định không đi qua . Gọi là một điểm thay đổi trên . Chứng minh rằng các mặt cầu tâm và bán kính luôn luôn đi qua một đường tròn cố định.Lời giải:
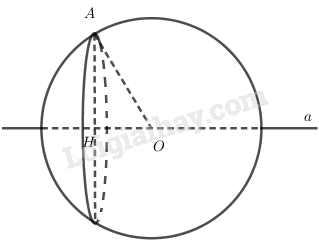
Xét mặt phẳng qua điểm và vuông góc với đường thẳng . Goi giao của với là điểm .
Xét mặt cầu tâm bán kính ; mặt cầu này giao với mặt phẳng theo đường tròn tâm là hình chiếu vuông góc của lên và bán kính cố định.
+) Công thức tính diện tích mặt cầu bán kính là:
+) Công thức tính thể tích mặt cầu bán kính là:
Lời giải: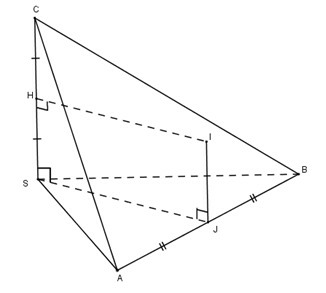
Gọi là tâm mặt cầu ngoại tiếp hình chóp tam giác . Hạ vuông góc , vì cách đều điểm nên cũng cách đều điểm .
Vì tam giác vuông đỉnh nên là trung điểm của .
Ta có
Do vuông góc nên .
Gọi là trung điểm , ta có nên .
Xét tứ giác ta có: do ;
do chứa ;
do chứa
Suy ra tứ giác là hình chữ nhật.
.
Do vậy, và bán kính hình cầu ngoại tiếp là
Diện tích mặt cầu là:
Do đó mọi điểm trên cách đều S,A,B. (Theo bài 3)
Dựng mặt phẳng trung trực của SC cắt tại I.
Khi đó ta có: .
. Vậy I là tâm đường tròn ngoại tiếp S.ABC
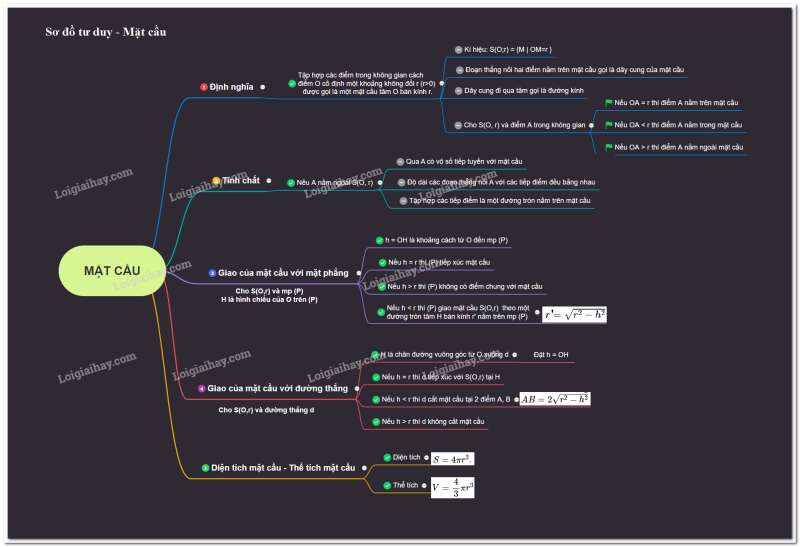
1. Định nghĩa
Tập hợp các điểm trong không gian cách điểm cố định một khoảng không đổi được gọi là một mặt cầu tâm bán kính .
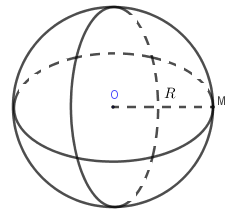
Kí hiệu:
* Cho mặt cầu và điểm trong không gian.
- Nếu thì điểm nằm trên mặt cầu
- Nếu thì điểm nằm trong mặt cầu.
- Nếu thì điểm nằm ngoài mặt cầu.
2. Tính chất
Nếu điểm ngoài mặt cầu thì:
- Qua có vô số tiếp tuyến với mặt cầu.
- Độ dài các đoạn thẳng nối với các tiếp điểm đều bằng nhau.
- Tập hợp các tiếp điểm là một đường tròn nằm trên mặt cầu.
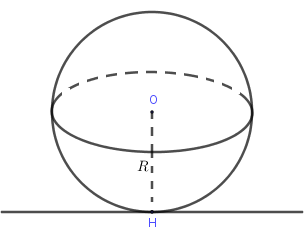
3. Giao của mặt cầu với mặt phẳng
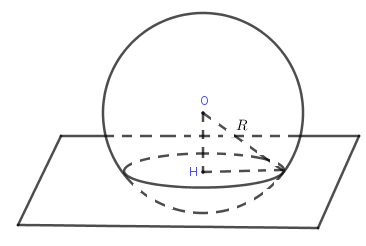
Cho mặt cầu tâm , bán kính và mặt phẳng , gọi là hình chiếu của trên .
+ Nếu thì cắt theo đường tròn tâm và bán kình .
+ Nếu thì tiếp xúc tại tiếp điểm .
+ Nếu thì và không có điểm chung.
Đặc biệt: Nếu thì đường tròn giao tuyến của và được gọi là đường tròn lớn, được gọi là mặt phẳng kính.
4. Giao của mặt cầu với đường thẳng.
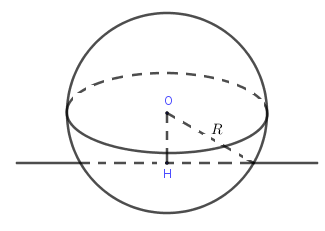
Cho mặt cầu tâm , bán kính và đường thẳng , gọi là hình chiếu của trên .
+ Nếu thì cắt tại điểm phân biệt.
+ Nếu thì cắt tại một điểm duy nhất . ( là tiếp tuyến với mặt cầu, là tiếp điểm)
+ Nếu thì và không có điểm chung.
5. Tiếp tuyến với mặt cầu (Đọc thêm)
- Qua một điểm nằm trong mặt cầu không vẽ được tiếp tuyến nào với mặt cầu.
- Qua một điểm nằm trên mặt cầu vẽ được vô số tiếp tuyến với mặt cầu tại điểm đó. Tập hợp các tiếp tuyến chính là mặt phẳng tiếp diện của mặt cầu.
- Qua một điểm nằm ngoài mặt cầu vẽ được vô số tiếp tuyến với mặt cầu. Tập hợp các tiếp điểm với mặt cầu là đường tròn nằm trên mặt cầu.
6. Công thức diện tích mặt cầu và thể tích hình cầu
1. Các khái niệm cơ bản
- Mặt cầu ngoại tiếp hình đa diện nếu nó đi qua mọi đỉnh của đa diện.
- Mặt cầu nội tiếp hình đa diện nếu nó tiếp xúc với mọi mặt của đa diện.
- Trục đa giác đáy là đường thẳng đi qua tâm đường tròn ngoại tiếp đa giác đáy và vuông góc với mặt phẳng chứa đa giác đáy.
+ Mọi điểm nằm trên trục đa giác đáy thì cách đều các đỉnh của đa giác đáy và ngược lại.
- Mặt phẳng trung trực của đoạn thẳng: là mặt phẳng đi qua trung điểm của đoạn thẳng và vuông góc với đoạn
thẳng đó.
+ Mọi điểm nằm trên mặt phẳng trung trực của đoạn thẳng thì cách đều hai đầu mút của đoạn thẳng và ngược lại.
2. Mặt cầu nội, ngoại tiếp một số đa diện cơ bản
- Hình hộp chữ nhật có mặt cầu ngoại tiếp, hình lập phương có cả mặt cầu ngoại tiếp và mặt cầu nội tiếp.
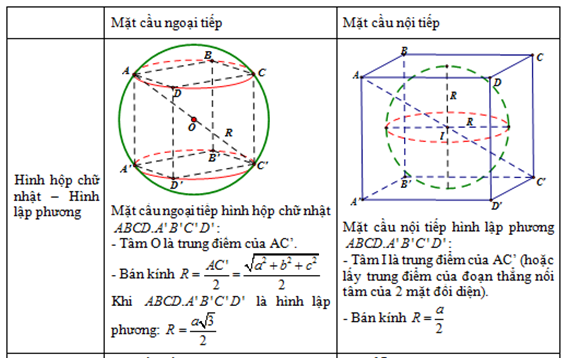
- Hình chóp nội tiếp được mặt cầu nếu và chỉ nếu đáy của nó là đa giác nội tiếp được đường tròn.
+ Hình chóp có các đỉnh nhìn đoạn thẳng nối hai đỉnh còn lại dưới một góc vuông.
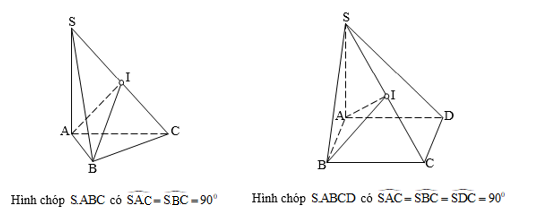
- Hình chóp đều:
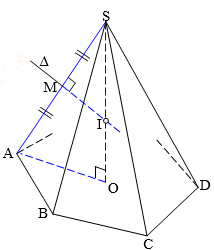
Bán kính: với là độ dài cạnh bên,
là chiều cao hình chóp.
- Hình chóp có cạnh bên vuông góc với đáy:
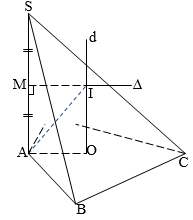
Bán kính với là bán kính đường tròn đáy, là chiều cao hình chóp.
Đặc biệt: tứ diện vuông: với là ba cạnh bên xuất phát từ đỉnh các góc vuông.
- Lăng trụ nội tiếp được mặt cầu nếu nó là lăng trụ đứng và đáy là đa giác nội tiếp được đường tròn.
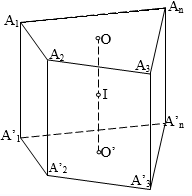
Bán kính với là bán kính đường tròn đáy, là chiều cao lăng trụ đứng.
3. Công thức tính diện tích mặt cầu, thể tích khối cầu
Cho mặt cầu có bán kính , khi đó:
- Công thức tính diện tích mặt cầu:
- Công thức tính thể tích khối cầu:

