Giải Toán 12 Bài 1: Hệ tọa độ trong không gian

75 lượt xem

Bài trước

Bài sau

Chúng tôi giới thiệu Giải bài tập Toán lớp 12 Bài 1: Hệ tọa độ trong không gian chính xác, chi tiết nhất giúp học sinh dễ dàng làm bài tập Hệ tọa độ trong không gian lớp 12.

Giải bài tập Toán lớp 12 Bài 1: Hệ tọa độ trong không gian

Trả lời câu hỏi giữa bài

Trả lời câu hỏi 1 trang 63 SGK Hình học 12: Trong không gian

O x y z

, cho một điểm

M

. Hãy phân tích vecto

\vec{O M}

theo ba vecto không đồng phẳng

\vec{i}; \vec{j}; \vec{k}

đã cho trên các trục

O x, O y, O z

Phương pháp giải:

+ nếu $M (x, y, z) \Rightarrow \vec{O M} (x, y, z)$

+ Vecto $\vec{O M}$ có toa độ $(x, y, z)$ tức là: $\vec{O M} (x, y, z) = x . \vec{i} + y . \vec{j} + z . \vec{k}$ với $\vec{i}; \vec{j}; \vec{k}$ lần lượt là các vecto đơn vị của $O x, O y, O z$

Lời giải:

Gọi tọa độ của $M$ trong không gian là $(x, y, z)$

$\Rightarrow \vec{O M} (x, y, z)$ hay $\vec{O M} = x \vec{i} + y \vec{j} + z \vec{k}$

Trả lời câu hỏi 2 trang 64 SGK Hình học 12: Trong không gian

O x y z

, cho hình hộp chữ nhật

A B C D . A^{'} B^{'} C^{'} D^{'}

có đỉnh

A

trùng với gốc

O

, có

\vec{A B}; \vec{A D}; \vec{{A A}^{'}}

theo thứ tự cùng hướng với

\vec{i}; \bar{j}; \vec{k}

và có

A B = a, A D = b, A A^{'} = c

. Hãy tính tọa độ các vecto

\vec{A B}; \vec{A C}; \vec{A C^{'}}; \vec{A M}

với

M

là trung điểm của cạnh

C^{'} D^{'}

Phương pháp giải:

Vẽ hình, xác định tọa độ các véc tơ.

+ Nếu A trùng với gốc tọa độ thì $\vec{A B}$ có tọa độ là tọa độ điểm $B$

+ Dựa vào độ dài cạnh để xác định tọa đô các đỉnh

Lời giải:

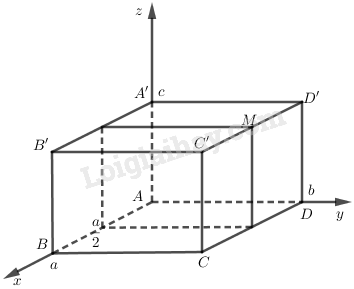
Ta có: $A (0; 0; 0)$ trùng với gốc tọa độ.

Vì $B \in A x nên B (a; 0; 0)$ (trong đó a là độ dài đại số của đoạn $A B$ )

Tương tự ta suy ra các đỉnh $D (0; b; 0), A^{'} (0; 0; c)$ .

Điểm $C$ thuộc mp $(A x y)$ nên tọa độ $C$ có dạng $(x, y, 0)$ trong đó $x$ là độ dài đại số của $A B$ , $y$ là độ dài đại số của $A D$

suy ra $C (a; b; 0)$

Tương tự ta suy ra $D^{'} (0; b; c),$ $B^{'} (a; 0; c)$

Riêng $C^{'} (a; b; c)$ , $M (\frac{a}{2}; b; c)$ .

Vậy $\vec{A B} = (a; 0; 0),$ $\vec{A C} = (a; b; 0),$ $\vec{A C^{'}} = (a; b; c)$ , $\vec{A M} = (\frac{a}{2}; b; c)$ .

Trả lời câu hỏi 3 trang 66 SGK Hình học 12: Với hệ tọa độ

O x y z

trong không gian, cho

\vec{a} = (3, 0, 1); \vec{b} = (1, - 1, - 2); \vec{c} = (2, 1, - 1)

. Hãy tính

\vec{a} . (\vec{b} + \vec{c}); | \vec{a} + \vec{b} |

Phương pháp giải:

Cho $\vec{a} (x, y, z) và \vec{b} (n, m, l)$

+ Cộng hai véc tơ: $\vec{a} + \vec{b} = (x + n, y + m, z + l)$

+ Nhân vô hướng: $\vec{a} . \vec{b} = x . n + y . m + z . l$

+ độ dài: $| \vec{a} | = \sqrt{x^{2} + y^{2} + z^{2}}$

Lời giải:

Ta có: $\vec{b} + \vec{c} = (1 + 2; - 1 + 1; (- 2) + (- 1)) = (3; 0; - 3)$ $\Rightarrow \vec{a} . (\vec{b} + \vec{c}) = 3.3 + 0.0 + 1. (- 3) = 6$

$\vec{a} + \vec{b} = (3 + 1; 0 + (- 1); 1 + (- 2)) = (4; - 1; - 1)$ $\Rightarrow | \vec{a} + \vec{b} | = \sqrt{4^{2} + {(- 1)}^{2} + {(- 1)}^{2}} = \sqrt{18} = 3 \sqrt{2}$

Trả lời câu hỏi 4 trang 67 SGK Hình học 12: Viết phương trình mặt cầu tâm

I (1; - 2; 3)

có bán kính

r = 5

Phương pháp giải:

Phương trình mặt cầu tâm $I (a; b; c)$ và bán kính $R$ có phương trình ${(x - a)}^{2} + {(y - b)}^{2} + {(z - c)}^{2} = R^{2}$

Lời giải:

Phương trình mặt cầu là: ${(x - 1)}^{2} + {(y + 2)}^{2} + {(z - 3)}^{2} = 5^{2} = 25$

Câu hỏi và bài tập (trang 68 SGK Hình học 12)

Bài 1 trang 68 SGK Hình học 12: Cho ba vectơ

\vec{a} (2; - 5; 3), \vec{b} (0; 2; - 1), \vec{c} (1; 7; 2)

a) Tính tọa độ của vectơ $\vec{d} = 4. \vec{a} - \frac{1}{3} \vec{b} + 3 \vec{c}$ .

b) Tính tọa độ của vectơ $\vec{e} = \vec{a} - 4 \vec{b} - 2 \vec{c}$ .

Phương pháp giải:

Cho $\vec{a} (a_{1}; a_{2}); a_{3} \vec{b} (b_{1}; b_{2}; b_{3})$ và $k \in R$ .

Khi đó:

$\begin{array}{l} k . \vec{a} = (k a_{1}; k a_{2}; k a_{3}) \\ \vec{a} \pm \vec{b} = (a_{1} \pm b_{1}; a_{2} \pm b_{2}; a_{3} \pm b_{3}) \end{array}$

Lời giải:

$\begin{array}{l} \vec{d} = 4 \vec{a} - \frac{1}{3} \vec{b} + 3 \vec{c} \\ \vec{d} = 4 (2; - 5; 3) - \frac{1}{3} (0; 2; - 1) + 3 (1; 7; 2) \\ \vec{d} = (8; - 20; 12) - (0; \frac{2}{3}; - \frac{1}{3}) + (3; 21; 6) \\ \vec{d} = (11; \frac{1}{3}; \frac{55}{3}) \end{array}$

$\begin{array}{l} \vec{e} = \vec{a} - 4 \vec{b} - 2 \vec{c} \\ \vec{e} = (2; - 5; 3) - 4 (0; 2; - 1) - 2 (1; 7; 2) \\ \vec{e} = (2; - 5; 3) - (0; 8; - 4) - (2; 14; 4) \\ \vec{e} = (0; - 27; 3) \end{array}$

Bài 2 trang 68 SGK Hình học 12: Cho ba điểm

A = (1; - 1; 1), B = (0; 1; 2), C = (1; 0; 1)

. Tìm tọa độ trọng tâm

G

của tam giác

A B C

Phương pháp giải:

$G$ là trọng tâm tam giác $A B C$ thì: ${\begin{cases} x_{G} = \frac{x_{A} + x_{B} + x_{C}}{3} \\ y_{G} = \frac{y_{A} + y_{B} + y_{C}}{3} \\ z_{G} = \frac{z_{A} + z_{B} + z_{C}}{3} \end{cases}$

Lời giải:

${\begin{cases} x_{G} = \frac{x_{A} + x_{B} + x_{C}}{3} = \frac{1 + 0 + 1}{3} = \frac{2}{3} \\ y_{G} = \frac{y_{A} + y_{B} + y_{C}}{3} = \frac{- 1 + 1 + 0}{3} = 0 \\ z_{G} = \frac{z_{A} + z_{B} + z_{C}}{3} = \frac{1 + 2 + 1}{3} = \frac{4}{3} \end{cases} \Rightarrow G (\frac{2}{3}; 0; \frac{4}{3})$

Bài 3 trang 68 SGK Hình học 12: Cho hình hộp

A B C D . A^{'} B^{'} C^{'} D^{'}

biết

A = (1; 0; 1), B = (2; 1; 2), D = (1; - 1; 1)

C^{'} (4; 5; - 5)

. Tính tọa độ các đỉnh còn lại của hình hộp.

Phương pháp giải:

Sử dụng các vector bằng nhau.

Hai vector $\vec{u} (x_{1}; y_{1}; z_{1}) = \vec{v} (x_{2}; y_{2}; z_{2}) \Leftrightarrow {\begin{cases} x_{1} = x_{2} \\ y_{1} = y_{2} \\ z_{1} = z_{2} \end{cases}$

Lời giải:

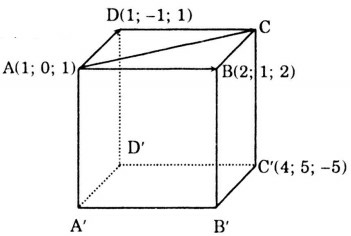
Ta có:

$\begin{aligned} \vec{A B} = (1; 1; 1) \\ \vec{A D} = (0; - 1; 0) \\ \vec{B C} = \vec{A D} \Leftrightarrow {\begin{matrix} x_{C} - 2 = 0 \\ y_{C} - 1 = - 1 \\ z_{C} - 2 = 0 \end{matrix} \Leftrightarrow {\begin{matrix} x_{C} = 2 \\ y_{C} = 0 \\ z_{C} = 2 \end{matrix} \end{aligned}$

Vậy $C = (2; 0; 2)$

Suy ra $\vec{C C^{'}} = (2; 5; - 7)$

Từ $\vec{A A^{'}} = \vec{B B^{'}} = \vec{D D^{'}} = \vec{C C^{'}} = (2; 5; - 7)$

Suy ra ${\begin{matrix} x_{A^{'}} - 1 = 2 \\ y_{A^{'}} - 0 = 5 \\ z_{A^{'}} - 1 = - 7 \end{matrix} \Leftrightarrow {\begin{matrix} x_{A^{'}} = 3 \\ y_{A^{'}} = 5 \\ z_{A^{'}} = - 6 \end{matrix}$

Vậy $A^{'} (3; 5; - 6)$

Tương tự

$\begin{array}{l} {\begin{cases} x_{B^{'}} - 2 = 2 \\ y_{B^{'}} - 1 = 5 \\ z_{B^{'}} - 2 = - 7 \end{cases} \Leftrightarrow {\begin{cases} x_{B^{'}} = 4 \\ y_{B^{'}} = 6 \\ z_{B^{'}} = - 5 \end{cases} \Rightarrow B^{'} (4; 6; - 5) \\ {\begin{cases} x_{D^{'}} - 1 = 2 \\ y_{D^{'}} + 1 = 5 \\ z_{D^{'}} - 1 = - 7 \end{cases} \Leftrightarrow {\begin{cases} x_{D^{'}} = 3 \\ y_{D^{'}} = 4 \\ z_{D^{'}} = - 6 \end{cases} \Rightarrow D^{'} (3; 4; - 6) \end{array}$

Bài 4 trang 68 SGK Hình học 12: Tính:

a) $\vec{a} . \vec{b}$ với $\vec{a} (3; 0; - 6)$ , $\vec{b} (2; - 4; 0)$ .

b) $\vec{c} . \vec{d}$ với $\vec{c} (1; - 5; 2)$ , $\vec{d} (4; 3; - 5)$ .

Phương pháp giải:

Tích vô hướng của 2 vector: $\vec{u} (x_{1}; y_{1}; z_{1}); \vec{v} (x_{2}; y_{2}; z_{2})$ $\Rightarrow \vec{u} . \vec{v} = x_{1} x_{2} + y_{1} y_{2} + z_{1} z_{2}$

Lời giải:

a) Ta có:

$\vec{a} . \vec{b} = 3.2 + 0. (- 4) + (- 6) .0 = 6$ .

b) Ta có:

$\vec{c} . \vec{d} = 1.4 + (- 5) .3 + 2. (- 5) = - 21$

Bài 5 trang 68 SGK Hình học 12: Tìm tâm và bán kính của các mặt cầu có phương trình sau đây:

a) $x^{2} + y^{2} + z^{2} - 8 x - 2 y + 1 = 0$ ;

b) $3 x^{2} + 3 y^{2} + 3 z^{2} - 6 x + 8 y + 15 z - 3 = 0$

Phương pháp giải:

Cách 1: Đưa phương trình về dạng phương trình chính tắc: ${(x - a)}^{2} + {(y - b)}^{2} + {(z - c)}^{2} = R^{2}$ , suy ra tâm $I (a; b; c)$ và bán kính bằng $R$ .

Cách 2: Phương trình có dạng $x^{2} + y^{2} + z^{2} + 2 a x + 2 b y + 2 c z + d = 0 (a^{2} + b^{2} + c^{2} - d > 0)$ là phương trình mặt cầu có tâm $I (- a; - b; - c)$ và bán kính $R = \sqrt{a^{2} + b^{2} + c^{2} - d}$ .

Lời giải:

Cách 1: Ta có phương trình :

$\begin{array}{l} x^{2} + y^{2} + z^{2} - 8 x - 2 y + 1 = 0 \\ \Leftrightarrow x^{2} - 8 x + y^{2} - 2 y + z^{2} + 1 = 0 \\ \Leftrightarrow x^{2} - 8 x + 16 + y^{2} - 2 y + 1 + z^{2} = 16 \\ \Leftrightarrow {(x - 4)}^{2} + {(y - 1)}^{2} + z^{2} = 16 \end{array}$

$\Leftrightarrow {(x - 4)}^{2} + {(y - 1)}^{2} + z^{2} = 4^{2}$

Đây là mặt cầu tâm $I (4; 1; 0)$ và có bán kính $r = 4$ .

Cách 2: Ta có:

$\begin{array}{l} 2 a = - 8; 2 b = - 2; 2 c = 0; d = 1 \\ \Rightarrow a = - 4; b = - 1; c = 0; d = 1 \\ R^{2} = a^{2} + b^{2} + c^{2} - d = {(- 4)}^{2} + {(- 1)}^{2} + 0 - 1 = 16 \end{array}$

do đó đây là phương trình mặt cầu tâm $I (4; 1; 0)$ , bán kính $R = 4$ .

Cách 1:

Ta có phương trình:

$\begin{array}{l} 3 x^{2} + 3 y^{2} + 3 z^{2} - 6 x + 8 y + 15 z - 3 = 0 \\ \Leftrightarrow 3 x^{2} - 6 x + 3 y^{2} + 8 y + 3 z^{2} + 15 z - 3 = 0 \\ \Leftrightarrow x^{2} - 2 x + y^{2} + \frac{8}{3} y + z^{2} + 5 z - 1 = 0 \\ \Leftrightarrow (x^{2} - 2 x + 1) + [y^{2} + 2. \frac{4}{3} y + {(\frac{4}{3})}^{2}] \\ + [z^{2} + 2. \frac{5}{2} z + {(\frac{5}{2})}^{2}] - 1 - 1 - {(\frac{4}{3})}^{2} - {(\frac{5}{2})}^{2} = 0 \\ \Leftrightarrow {(x - 1)}^{2} + {(y + \frac{4}{3})}^{2} + {(z + \frac{5}{2})}^{2} - \frac{361}{36} = 0 \\ \Leftrightarrow {(x - 1)}^{2} + {(y + \frac{4}{3})}^{2} + {(z + \frac{5}{2})}^{2} = {(\frac{19}{6})}^{2} \end{array}$

Đây là mặt cầu tâm $J (1; - \frac{4}{3}; - \frac{5}{2})$ và có bán kính là $R = \frac{19}{6}$ .

Cách 2:

Xét phương trình $3 x^{2} + 3 y^{2} + 3 z^{2} - 6 x + 8 y + 15 z - 3 = 0$

$\begin{array}{l} \Leftrightarrow x^{2} + y^{2} + z^{2} - 2 x + \frac{8}{3} y + 5 z - 1 = 0 \\ T a c ó : 2 a = - 1; 2 b = \frac{8}{3}; 2 c = 5; d = - 1 \\ \Rightarrow a = - 1; b = \frac{4}{3}; c = \frac{5}{2}; d = - 1 \\ R^{2} = a^{2} + b^{2} + c^{2} - d = {(- 1)}^{2} + {(\frac{4}{3})}^{2} + {(\frac{5}{2})}^{2} + 1 = \frac{361}{36} = {(\frac{19}{6})}^{2} \end{array}$

do đó đây là phương trình mặt cầu tâm $J (1; - \frac{4}{3}; - \frac{5}{2})$ , bán kính $R = \frac{19}{6}$ .

Bài 6 trang 68 SGK Hình học 12: Lập phương trình mặt cầu trong hai trường hợp sau đây:

a) Có đường kính $A B$ với $A (4; - 3; 7), B (2; 1; 3)$

b) Đi qua điểm $A = (5; - 2; 1)$ và có tâm $C (3; - 3; 1)$

Phương pháp giải:

a) Mặt cầu có tâm là trung điểm của $A B$ và bán kính bằng $\frac{A B}{2}$

b) Mặt cầu có tâm $C$ và bán kính bằng $C A$

Lời giải:

a) Gọi $I$ là trung điểm của $A B$ , thì mặt cầu có đường kính $A B$ , có tâm $I$ và bán kính $r = \frac{1}{2} A B = I A$ .

Ta có:

$\begin{array}{l} {\begin{cases} x_{I} = \frac{x_{A} + x_{B}}{2} = \frac{4 + 2}{2} = 3 \\ y_{I} = \frac{y_{A} + y_{B}}{2} = \frac{- 3 + 1}{2} = - 1 \\ z_{I} = \frac{z_{A} + z_{B}}{2} = \frac{7 + 3}{2} = 5 \end{cases} \Rightarrow I (3; - 1; 5) \\ A B = \sqrt{{(2 - 4)}^{2} + {(1 + 3)}^{2} + {(3 - 7)}^{2}} = 6 \Rightarrow R = \frac{A B}{2} = 3 \end{array}$

Do vậy phương trình mặt cầu đường kính $A B$ có dạng: ${(x - 3)}^{2} + {(y + 1)}^{2} + {(z - 5)}^{2} = 9$

b) Mặt cầu cần tìm có tâm $C (3; - 3; 1)$ và có bán kính $R = C A = \sqrt{{(3 - 5)}^{2} + {(- 3 + 2)}^{2} + {(1 - 1)}^{2}} = \sqrt{5}$

Do đó phương trình mặt cầu có dạng: ${(x - 3)}^{2} + {(y + 3)}^{2} + {(z - 1)}^{2} = 5$ .

Lý thuyết Bài 1: Hệ tọa độ trong không gian

1. Hệ tọa độ trong không gian

Trong không gian cho ba trục tọa độ chung gốc $O$ , đôi một vuông góc với nhau $x^{'} O x; y^{'} O y; z^{'} O z$ . Hệ ba trục tọa độ như vậy được gọi là hệ trục tọa độ Đề-các vuông góc $O x y z$ ; $O$ là gốc tọa tọa độ. Giả sử $\vec{i}, \vec{j}, \vec{k}$ lần lượt là các vectơ đơn vị trên các trục $x^{'} O x, y^{'} O y, z^{'} O z$ (h. 52)

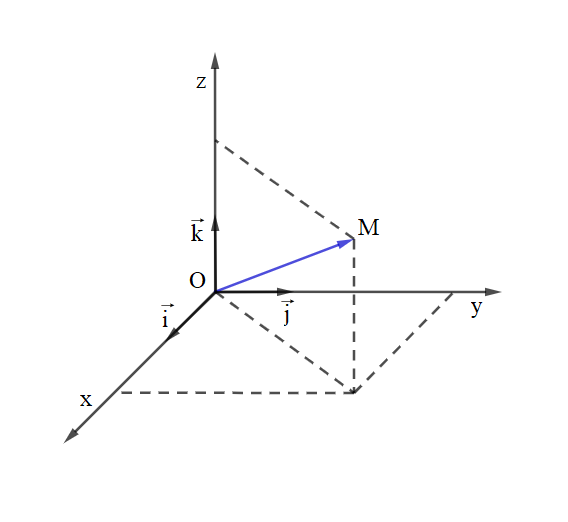
Với điểm $M$ thuộc không gian $O x y z$ thì tồn tại duy nhất bộ số $(x; y; z)$ để

$\vec{O M} = x . \vec{i} + y . \vec{j} + z . \vec{k}$ ,

bộ $(x; y; z)$ được gọi là tọa độ của điểm $M (x; y; z)$ .

Trong không gian Oxyz cho vectơ $\vec{a}$ , khi đó $\vec{a} = a_{1} \vec{i} + a_{2} \vec{j} + a_{3} \vec{k}$

Ta viết $\vec{a}$ $(a_{1}; a_{2}; a_{3})$ và nói $\vec{a}$ có tọa độ $(a_{1}; a_{2}; a_{3})$ .

2. Biểu thức tọa độ của các phép toán vectơ

Giả sử $\vec{a}$ = $(a_{1}; a_{2}; a_{3})$ và $\vec{b}$ = $(b_{1}; b_{2}; b_{3})$ , thì:

$\vec{a} + \vec{b}$ $= (a_{1} + b_{1}; a_{2} + b_{2}; a_{3} + b_{3}) .$

$\vec{a} - \vec{b}$ $= (a_{1} - b_{1}; a_{2} - b_{2}; a_{3} - b_{3}) .$

$k . \vec{a}$ $= (k a_{1}; k a_{2}; k a_{3}) .$

3. Tích vô hướng

Cho $\vec{a}$ $(a_{1}; a_{2}; a_{3})$ và $\vec{b}$ $(b_{1}; b_{2}; b_{3})$ thì tích vô hướng $\vec{a}$ . $\vec{b}$ $= a_{1} . b_{1} + a_{2} . b_{2} + a_{3} . b_{3}$

Ta có: $| \vec{a} | = \sqrt{a_{1}^{2} + a_{2}^{2} + a_{3}^{2}} .$

Đặt $φ = (\hat{\vec{a}, \vec{b}})$ , 0 ≤ $φ$ ≤ 1800 thì $c o s φ = \frac{a_{1} b_{1} + a_{2} b_{2} + a_{3} b_{3}}{\sqrt{a_{1}^{2} + a_{2}^{2} + a_{3}^{2}} \sqrt{b_{1}^{2} + b_{2}^{2} + b_{3}^{2}}}$ (với $\vec{a}$ ≠ $\vec{0}$ , $\vec{b}$ ≠ $\vec{0}$ )

4. Phương trình mặt cầu

Trong không gian $O x y z$ , mặt cầu $(S)$ tâm $I (a; b; c)$ bán kính $R$ có phương trình chính tắc ${(x - a)}^{2} + {(y - b)}^{2} + {(z - c)}^{2} = R^{2}$

Mặt cầu có phương trình tổng quát $x^{2} + y^{2} + z^{2} + 2 a x + 2 b y + 2 c z + d = 0$ có tâm $I (- a; - b; - c)$ và bán kính $R = \sqrt{a^{2} + b^{2} + c^{2} - d}$

Các dạng toán về điểm và vecto trong không gian

Dạng 1: Tìm tọa độ điểm đặc biệt.

Phương pháp:

Sử dụng định nghĩa điểm, điểm thuộc các trục tọa độ, điểm thuộc các mặt phẳng tọa độ và các tọa độ điểm đặc biệt như:

- Trung điểm $M (\frac{x_{A} + x_{B}}{2}; \frac{y_{A} + y_{B}}{2}; \frac{z_{A} + z_{B}}{2})$

- Trọng tâm tam giác $G (\frac{x_{A} + x_{B} + x_{C}}{3}; \frac{y_{A} + y_{B} + y_{C}}{3}; \frac{z_{A} + z_{B} + z_{C}}{3})$

- Trọng tâm tứ diện

$(\frac{x_{A} + x_{B} + x_{C} + x_{D}}{4}; \frac{y_{A} + y_{B} + y_{C} + y_{D}}{4}; \frac{z_{A} + z_{B} + z_{C} + z_{D}}{4})$

Dạng 2: Tìm mối quan hệ giữa các véc tơ.

Phương pháp chung:

Sử dụng các lý thuyết về véc tơ bằng nhau, cùng phương, vuông góc, đồng phẳng,… để xét mối quan hệ giữa các véc tơ.

Dạng 3: Ứng dụng tích có hướng để tính diện tích, thể tích.

Phương pháp:

Sử dụng các công thức diện tích, thể tích để tính.

Dạng 4: Tìm tọa độ điểm thỏa mãn điều kiện cho trước.

Phương pháp:

- Bước 1: Gọi tọa độ điểm theo tham số (thường là thuộc đường thẳng, thuộc mặt phẳng,…).

- Bước 2: Thay tọa độ điểm vào điều kiện đề bài để tìm tham số, từ đó ta được kết quả cần tìm.

Xem thêm các chương trình khác:

Bài trước

Bài sau

Giải SGK, SBT, Chuyên đề Toán Học Lớp 12

Giải Toán 12 Bài 1: Hệ tọa độ trong không gian

Xem thêm các chương trình khác: